Раздельное резервирование

Логическая схема устройства представлена на рис. 4.2,б.

При раздельном резервировании вероятность безотказной работы системы

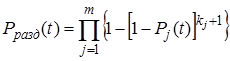, (4.17)

где P_j(t) – вероятность безотказной работы j–го элемента (участка резервирования) в течении наработки (0, t); m – число участков резервирования; (k_j+1) – число параллельно соединенных на логической схеме элементов в j–м участке резервирования.

При равнонадежных элементах и показательном распределении наработки до отказа

- вероятность безотказной работы

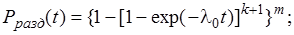(4.18)

- средняя наработка до отказа

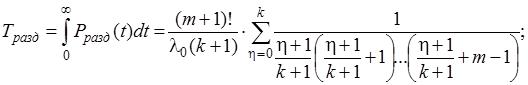(4.19)

- интенсивность отказов

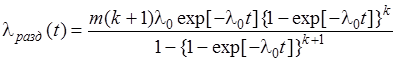. (4.20)

В случае, когда 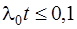, имеем:

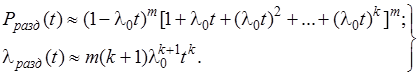(4.21)

4.4.1.3. Общее резервирование с дробной кратностью

При общем резервировании с дробной кратностью для определения вероятности безотказной работы системы используется биномиальный закон распределения.

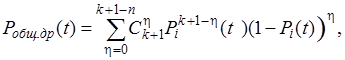(4.22)

где η – количество отказавших устройств, при которых резервированная система остается работоспособной ( η = 0,1,…, (к+1-n),

n- необходимое число работоспособных устройств из общего числа (к+1) устройств,

P_i(t) – вероятность безотказной работы основного или любого резервного устройства в течение наработки (0, t).

При показательном распределении наработки до отказа:

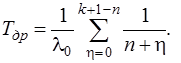(4.23)

При резервировании элементов с двумя видами от­казов (обрыв и короткое замыкание) рассматривают не логические, а электрические схемы соединений элемен­тов.

Вероятность обрыва и короткого замыкания обозна­чим соответственно q₀(t) и q_S(t).

Для расчета Q(t) - вероятности от­каза схемы с учетом двух видов отказов элементов составляется таблица всех возможных вариантов состоя­ний элементов схемы, выделяются комбинации, при ко­торых схема не работает, вычисляются и суммируются вероятности появления этих комбинаций.

Для схем (например, релейно-контактных), опреде­ленный вид отказа которых может быть вызван лишь од­ноименным видом отказа элемента, вероятность отказа определяется по формуле

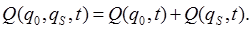
При последовательном электрическомсоединения m элементов

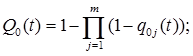(4.24)

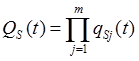. (4.25)

При параллельном электрическом соединении k +1элементов

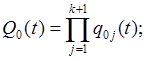(4.26)

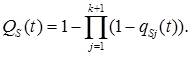(4.27)

4.4.2. Резервирова­ние замещением ненагруженное и облегченное с абсолютно надёжными переключателями

4.4.2.1.Общее ненагруженное резервирование замещением

Рассмот­рим случай общего резервирования. Считаем, что резервные системы не могут отказывать до момента их включения в работу, также предполагаем, что индикаторы состояния основной или резервных цепей идеальны.

При раздельном ре­зервировании приведенные ниже формулы справедливы для отдельных участков резервированной схемы.

Резервированная система будет безотказно работать на отрезке времени [0, t] при следующих возможных событиях:

1) основная система не отказала на интервале времени [0, t],

2) работающая система отказала на интервале времени [τ, τ+Δτ], где

τ < t, Δτ→ 0, но работоспособный резервный элемент включился в работу и безотказно отработал интервал времени [τ, t- τ].

При принятых допущениях вероятность безотказной работы системы, имеющей одно основное и kрезервных устройств, вычисляется по рекуррентной формуле

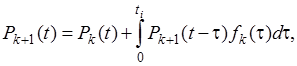(4.28)

где P_k(t)—вероятность безотказной работы системы, имеющей одно основное и k - 1 резервных устройств; P_(k+1)(t - τ) - вероятность безотказной работы (k+1)-го резервного устройства в течение наработки

(t - τ) при условии, что до момента τэто устройство бы­ло работоспособно; f_k(τ) - плотность распределения на­работки до отказа системы, имеющей одно основное и k - 1 резервных устройств.

В случае показательного распределения наработки до отказа и равнонадежных элементах имеет место простейший поток отказов и вероятность безотказной работы системы определяется ситуацией, когда в резервированной системе число отказавших цепей η <= k (используем закон Пуассона):

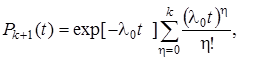(4.29)

где λ₀ - интенсивность отказов одного из k+1 парал­лельно соединенных на схеме резервирования устройств.

Средняя наработка до отказа

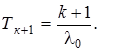(4.30)

Так как при ненагруженном резерве значения нара­ботки τ₁, τ₂, … τ_k+1 системы в состояниях 1, 2, ..., (k+1) можно считать независимыми случайными величинами, при (k+1) ≥ 5 распределение наработки до отказа ре­зервированной системы будет практически нормальным.