Билет №53. Как можно представить неопределенность знаний с помощью правила Байеса? Какова, при этом, вычислительная сложность получения оценки вероятности?

Для представления неопределенности знаний можно весьма эффективно использовать положения теории вероятностей. Подобные представления базируются на понятии условной вероятности. Как следует из определения, условная вероятность события d при данном s – это

вероятность того, что событие d наступит при условии, что наступило событие s. Например, условной вероятностью является вероятность того, что у пациента действительно имеется заболевание d, если у него обнаружен только симптом s. Для вычисления условной вероятности

используется следующая формула:

Как видно из данной формулы, условная вероятность определяется через понятие совместности или одновременности событий, то есть вероятности совпадения событий d и s, разделенное на вероятность события s. Из приведенной формулы очевидно, что вероятность совпадения или произведения двух событий равна произведению вероятности одного из них и условной вероятности другого, вычисленную при условии, что первое имело место:

P(d Ù s)= P(s) * P(d | s) или

P(d Ù s)= P(d)* P(s | d).

Подставляя последнюю формулу в определение условной вероятности можно получить правило Байеса в простейшем виде:

Это правило позволяет определить вероятность P(d | s) появления события d при условии, что произошло событие s через заранее известную условную вероятность P(s | d). В полученном выражении P(d) – априорная вероятность наступления события d, а P(d | s) – апостериорная вероятность, то есть вероятность того, что событие d произойдет, если известно, что событие s свершилось. Данное правило иногда называют инверсной формулой для условной вероятности, так как она позволяет вычислить вероятность P(d | s) через P(s | d).

Для систем, основанных на знаниях, правило Байеса гораздо удобнее формулы определения условной вероятности через вероятность одновременного наступления событий P(d ∧ s). В этом достаточно просто убедится. Пусть у пациента X имеется некоторый симптом симптом_Y и

необходимо узнать, какова вероятность того, что этот симптом является следствием заболевания заболевание_Z. Для того чтобы непосредственно вычислить P(заболевание_Z | симптом_Y), нужно оценить каким либо образом, сколько человек в мире страдают этим заболеванием, и сколько

человек одновременно имеют заболевание_Z и симптом_Y. Такая информация, как правило, недоступна или отсутствует вообще. Особенно, что касается вычисления P(заболевание_Z Ù симптом_Y).

Однако, если посмотреть на вероятность не как на объективную частотность событий при достаточно долгих независимых испытаниях, а как на субъективную оценку совместного наступления событий, то ситуация значительно упрощается. Например, врач может не знать или не иметь возможности определить, какая часть пациентов имеющих симптом_Y страдают от заболевание_Z. Но на основании, например собственного опыта или литературных данных, врач в состоянии оценить у какой части пациентов имеющих заболевание_Z встречается симптом_Y.

Следовательно, можно вычислить P(симптом_Y | заболевание_Z) и применить инверсную формулу для условной вероятности.

Ситуация значительно усложняется, если речь пойдет о множестве симптомов и множестве заболеваний. Если необходимо вычислить условную вероятность для одного симптома из некоторого множества симптомов, то потребуется m*n + m + n вычислений, где m – количество

возможных диагнозов, а n – число разнообразных симптомов. Учитывая, что в медицинской диагностике используются тысячи видов заболеваний и огромное количество симптомов, эта задача становится нетривиальной.

Ситуация еще усложниться, если включить в процесс постановки диагноза сразу несколько симптомов. Правило Байеса в обобщенной форме выглядит следующим образом:

Данная формула требует (m*n)^k + m + n^k вычислений оценок вероятностей, что даже при небольшом k является большим числом. Такое количество оценок требуется по той причине, что для вычисления P(s1 Ù … Ù sk) в общем случае сначала требуется вычислить P(s1|s2 Ù … Ù sk) *

P(s2|s3Ù … Ù sk)*…*P(sk). Однако если предположить что симптомы независимы, то количество вычислений резко снижается и становиться таким же, как и в случае учета единственного симптома, так как в для независимых si и sj P(si Ù sj) = P(si) * P(sj). Даже, если в действительности

установить независимость невозможно, можно предположить наличие так называемой условной независимости. Это предположение может основываться на каких-либо фоновых знаниях. Например, если в автомобиле нет бензина и не работает свет, то исходя из общих представлений о конструкции автомобиля можно предположить, что эти симптомы независимы. Но если автомобиль не заводится и не работает освещение, то такое предположение сделать уже нельзя. Соответственно, в системе, использующей вероятностные оценки достоверности, необходимо

предусмотреть средства отслеживания зависимости между используемыми данными.

Билет №54. В чем заключается отличие нечетких множеств от обычных «жестких» множеств? Приведите пример описания нечеткого понятия и множества, построенного на этом понятии. Как определяются нечеткие операции «отрицание», «логическое и» и «логическое или» в нечеткой логике? Изложите основную идею теории возможности. Приведите пример описания нечеткой вероятности.

Классическая теория множеств базируется на булевой, двухзначной логике. Принадлежность объекта к классу а ∈ А может принимать значения ИСТИНА, если объект а входит в множество А, или ЛОЖЬ – в противоположном случае.

Суть теории нечетких множеств лучше всего рассмотреть на примере. Возьмем в качестве нечеткой категории понятие «быстрый» Если применить его к автомобилям, то тогда возникает вопрос: какой автомобиль можно считать быстрым. В классической теории множество А «быстрых автомобилей» можно сформировать либо перечислением конкретных представителей данного класса, либо введя в рассмотрение характеристическую функцию f, такую, что для любого объекта X

f(X) = ИСТИНА тогда и только тогда, когда X Î A.

Например, эта функция может отбирать только те автомобили, которые могут развивать скорость более 150 км в час:

ИСТИНА если CAR (X) и MAX SPEED(X) > 150

GT150(X) = ЛОЖЬ, в противном случае

Эта функция, используя предикат CAR(X) и функцию MAX_SPEED(X) представляет множество:

{ X Î CAR | MAX_SPEED(X) > 150 }.

Эта формула утверждает, что элементами нового множества являются только те элементы множества CAR, для которых максимальная скорость превышает 150 км в час. Представляя все множество «быстрых» автомобилей, интуитивно кажется, что границы этого множества должны быть размыты, а принадлежность элементов этому множеству может быть каким либо образом ранжирована. Можно говорить, что каждый элемент (автомобиль) множества «быстрых» автомобилей более или менее типичен для данной категории. Следовательно, с помощью некоторой функции можно выразить степень принадлежность элемента к множеству. Пусть функция f (X) определена на интервале [0, 1]. Тогда, если для объекта X функция f(X) = 1, то этот объект определенно является членом множества, а если для него f(X) = 0, то он определенно не является членом множества. Все промежуточные значения f(X) выражают степень принадлежности к множеству. В примере с автомобилями требуется функция, оперирующая со скоростью. Ее можно определить таким образом, что fFAST(80) = 0 и fFAST(180) = 1, а все

промежуточные значения представляются некоторой монотонной кривой, имеющей значения в интервале [0, 1].

Для определения множества FAST_CAR «быстрых» автомобилей, на основании приведенной выше функции можно ввести новую характеристическую функцию, определенную на множестве всех

автомобилей:

f_{FAST_CAR}(X) = f _FAST(MAX_SPEED(X)).

Членами этого множества, таким образом, становятся пары (объект, степень), например:

FAST_CAR = {(Porshe 944, 0,9), (BMW 316, 0,6), (Chevy NIVA, 0,1)}.

Для вычисления значений сложных выражений принадлежности элементов к множеству в классической теории множеств используется булева логика. Для нечетких множеств, принадлежность к которым выражается функцией, принимающей значения от 0 до 1, была создана нечеткая логика. Аппарат этой логики включает операции отрицания, конъюнкции, дизъюнкции и пр., учитывающие концепцию неопределенности.

Например, логическое отрицание, по аналогии с теорией вероятности, реализуется в виде выражения: F(X) = 1 - F(X), где F – нечеткий предикат (нечеткая функция).

Аналоги операций конъюнкции и дизъюнкции в нечеткой логике не связаны с теорией вероятности и имеют следующие определения:

f _{F ∧ G}(X) = min(f _F(X), f _G(X)),

f _{F ∨ G}(X) = max(f _F(X), f _G(X)).

Например, фраза «Porshe 944 является быстрым и представительским автомобилем» может быть представлена с помощью предикатов FAST_CAR(Porshe-944) и PRETENTIOUS_CAR(Porshe-944). Значение FAST_CAR(Porshe-944) = 0,9, а значение PRETENTIOUS_CAR(Porshe-944) пусть будет равно 0,7. Соответственно, можно вычислить значение конъюнкции этих предикатов:

FAST_CAR(Porshe-944) ∧ PRETENTIOUS_CAR(Porshe-944)=

=min(0,9, 0,7)=0,7.

Интересным следствием из приведенных выше определений операций нечеткой логики является следующий пример:

FAST_CAR(Porshe-944) ∧ FAST_CAR(Porshe-944) = 0,1.

Очевидно, значение условной вероятности того, что это утверждение является истинным равно нулю:

P(FAST_CAR(Porshe-944) | FAST_CAR(Porshe-944)) = 0.

Однако в нечеткой логике это выражение вычисляется как min (0,9, 1 - 0,9) = 0,1. Смысл того, что это значение не равно нулю как раз и заключается в нечеткости понятия «быстрый». Кроме «быстрых» автомобилей существуют также «медленные» и «средние». Выражение FAST_CAR(Porshe-944) = 0,9 означает, что можно только с 90% уверенностью отнести этот автомобиль к категории «быстрый», так как существуют еще, например, и более быстрые автомобили, принимающие участия в соревнованиях Формулы 1. Поэтому полученное значение 0,1 говорит о том, что Porshe-944 принадлежит также и категории «среднескоростных» автомобилей, которые в чем-то близки к «быстрым», а в чем-то к «медленным».

Одним из направлений в нечеткой логике является теория возможности, рассматривающая точно поставленные вопросы на нечетко сформулированных знаниях. Примером такого вопроса является утверждение «Вероятно, что X связан с Y». Существование объектов X и Y не вызывает сомнений, а вот наличие между ними связи ставится под вопрос.

Основные идеи теории возможности лучше всего рассмотреть на примере. Предположим, что в ящике находится 10 шаров, но известно, что только несколько из них являются красными. Какова вероятность того, что из ящика будет извлечен красный шар? Непосредственно вычислить эту

вероятность невозможно, так как нам известно, только, что красных шаров несколько, а сколько именно не задано. Тем не менее, для каждого значения вероятности P(RED) того, что шар является красным можно определить некоторое значение в диапазоне [0, 1]. Для этого следует определить понятие «несколько», как нечеткое множество, например: f_SEVERAL = {(2, 0.1), (3, 0.2), (4, 0.6), (5, 1.0), (6, 1.0), (7, 0.6), (8, 0.3) , (9, 0.1)}.

Из этого определения следует, что 3 из 10 с небольшой вероятностью можно считать синонимом «несколько», так как f_SEVERAL(3) = 0.2. Числа 5, 6 полностью согласуются с термином «несколько», а числа 1 и 10 не рассматриваются вовсе, как соответствующие этому понятию. Нечеткое множество, определенное на множестве чисел получило название нечеткие числа. Аналогичным образом можно определить нечеткие множества для понятий «мало», «почти» и пр. Распределение возможностей теперь можно вычислить по формуле

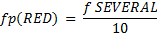
Подставляя в данную формулу множество, определенное выше получается новое множество:

{(0.2,0.1), (0.3,0.2), (0.4,0.6), (0.5,1.0), (0.6,1.0), (0.7,0.6), (0.8,0.3) , (0.9,0.1)}.

Таким образом, возможность того, что P(RED) = 0.3 составляет 20%. Множество f_P(RED) также называют нечеткой вероятностью.

С помощью данного механизма можно ввести в рассмотрение любую функцию, поэтому удобно использовать понятие нечеткого правдоподобия. Например, некоторое утверждение может быть оценено как «очень правдоподобное» или «частично правдоподобное». Эти понятия представляются на множестве, где областью определения и областью значений функции являются значения правдоподобия в нечеткой логике fTRUE: [0, 1]→[0, 1]. Следовательно, можно рассматривать значения, меньшие единицы, как «достаточно правдоподобные». Например, для

ситуации с быстрыми автомобилями можно определить

TRUE(FAST_CAR(Porsche-944)) = 1.

Таким образом, можно с полной уверенностью утверждать, что Porsche-944 является быстрым автомобилем, несмотря на то, что на рынке имеются и более скоростные автомобили.

Билет №55. Приведите пример множества гипотез, функций доверия и сомнения, а также оценки привлекательности для этого множества в соответствии с положениями теории обоснования Демпстера-Шефера. Объясните различие между понятиями «неуверенности» и «незнания» с точки зрения теории Демпстера-Шефера.

В теории Демпстера—Шефера (Dempster—Shafer) предполагается, что гипотезы —

компоненты пространства гипотез 6 — являются взаимно исключающими, а набор гипотез —

исчерпывающим. В терминологии авторов пространство гипотез 0 называется областью

анализа (frame of discernment). Также предполагается, что мы располагаем средством

получения свидетельств не только в пользу отдельных гипотез h1.....hn, принадлежащих 6, но и

в пользу подмножеств гипотез A1 ..., Ak, которые могут перекрываться.

Можно рассматривать эти свидетельства как элементы множества U и построить

отображение

Г:U -> 2⁰,

которое будет связывать каждый элемент в U с подмножеством пространства в. Такое

подмножество называется фокальным элементом. Отметим, что предположение об

исчерпывающей полноте набора гипотез означает, что ни один из элементов u U не

отображается на пустое множество. Другими словами, для любого свидетельства существует

хотя бы одна гипотеза, достоверность которой подтверждает это свидетельство.

Теория Демпстера—Шефера предлагает средства вычисления функции доверия на таких

множествах гипотез и правила объединения функций доверия, сформулированных на

основании разных свидетельств.

В теории Демпстера—Шефера т — это функция присвоения базовых вероятностей (bра —

basic probability assignment), которая определена на множестве 2⁰ значений из интервала

[0,1], такая, что

m(пустое множество) = 0

и

S[(т(Аi) - 1];

суммирование выполняется по всем

A_i 2⁰ .

Суммарное доверие Bel для любого фокального элемента А может быть найдено

суммированием значений т по всем подмножествам в А. Таким образом, Bel является функцией,

определенной на множестве 2^е значений из интервала [0,1], такой, что

Bel(A) = S_{B Î А} m(B).

Ве1(0) всегда равно 1, независимо от значения т(O). Это следует из определения функции

присвоения базовых вероятностей. Соотношение Ве1(O) = 1 означает следующее: можно с

полной уверенностью утверждать, что в пространстве 0 обязательно имеется корректная

гипотеза, поскольку по определению набор гипотез является исчерпывающим. Значение m(O) отображает вес свидетельства, еще не учтенного в подмножествах, входящих в пространство 0. Значения Bel и т будут равны для множеств, состоящих из единственного элемента.

Оценка вероятности фокального элемента А будет ограничена снизу оценкой доверия к А, а

сверху — оценкой привлекательности А, которая равна 1 - Веl(A^с)> где A^с — дополнение к A.

Оценка привлекательности A, Рls(A), представляет степень совместимости свидетельства с

гипотезами в А и может быть вычислена по формуле

Рls(A)= S _{A^B не равно пустому множеству} m(B).

Поскольку определенная таким образом оценка привлекательности А есть не что иное, как

мера нашего недоверия к -A, то можно записать:

Рls (A) = 1 - Вel (-A).

Значение оценки привлекательности А можно рассматривать как предел, до которого можно

улучшить гипотезы из А при наличии свидетельств в пользу гипотез-конкурентов. Удобно

рассматривать информацию, содержащуюся в оценке Bel для данного подмножества, в виде

доверительного интервала в форме [Вel(A), Pls(A)]. Ширина интервала может служить оценкой

неуверенности в справедливости гипотез из А при имеющемся наборе свидетельств.

Правила Демпстера позволяют вычислить новое значение функции доверия по двум ее

значениям, базирующимся на разных наблюдениях. Обозначим Bel₁ и Веl₂ два значения

функции доверия, которым соответствуют два значения функции присвоения базовых

вероятностей т₁ и т_г. Правило позволяет вычислить новое значение т₁+т₂, а затем и новое

значение функции доверия Веl₁+ Веl₂, основываясь на определениях, приведенных выше.

Для гипотезы А значение т₁+т₂(А) есть сумма всех произведений в форме т₁(Х) m₂(Y), где X

и Y распространяются на все подмножества в в, пересечением которых является А. Если в

таблице пересечений будет обнаружен пустой элемент, выполняется нормализация. В

процедуре нормализации значение k определяется как сумма всех ненулевых значений,

присвоенных в множестве 0, затем т₁+т₂(0) присваивается значение нуль, а значения m1+m2

для всех других множеств гипотез делится на (1 - k).

Таким образом,

m₁+m₂= S_X^Y=A[m₁(X)m₂(Y)]/[1- S X^Y = пустое множество{m₁(X)m₂(Y)}]

Следует учитывать, что значения т₁ и m₂ сформированы по независимым источникам

свидетельств в пределах того же пространства гипотез. Обратите внимание и на тот факт, что

вследствие коммутативности операции умножения правило Демпстера дает один и тот же

результат при любом порядке объединения свидетельств.