Оценка и учет погрешностей при точных измерениях

Основной постулат метрологии – отcчет является случайным числом.

При выполнении точных измерений пользуются средствами измерений повышенной точности, а вместе с тем применяют и более совершенные методы измерений. Во всяком измерении имеются случайныепогрешности. Поэтому вместо истинного значения измеряемой величины, принимается некоторое среднее арифметической значение (математическое ожидание). При большом числе измерений, как показывает теория вероятности и математической статистики, у нас есть обоснованная уверенность считать, что математическое ожидание является наилучшим приближением к истинному значению.

Теория случайных погрешностей основывается на двух аксиомах, базирующихся на опытных данных.

Аксиома случайности – при очень большом числе измерений случайные погрешности, равные по величине, но различные по знаку встречаются одинаково часто, т. е. число отрицательных погрешностей равно числу положительных.

Аксиома распределения – малые погрешности случаются чаще, чем большие. Очень большие погрешности не встречаются.

Пусть X неизвестное истинное значение некоторой неизвестной физической величины. При измерении этой величины получено n независимых друг от друга результатов наблюдений x₁, x₂,…x_n.

Измерения выполнены одним и тем же прибором и с одинаковой тщательностью, т. е. одинаково точными и свободными от систематической погрешности. Предположим, что каждому измерению сопутствует случайная погрешность 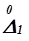, ,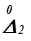… 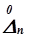– различная по значению и по знаку. Следовательно:

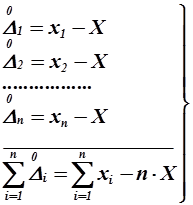(1.33)

где 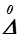– случайная величина погрешности, среднее значение которой равно нулю.

На основании аксиомы случайности можно предположить, что в выполненных измерениях число, сумма и числовые значения положительных случайных погрешностей приблизительно равны числу, сумме и значениям отрицательных погрешностей. Другими словами; распределение случайных погрешностей – равностороннее по отношению к среднему значению измеряемой величины X. Таким образом, по предположению,

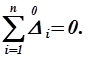(1.34)

Отсюда

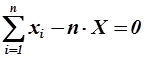(1.35)

и поэтому

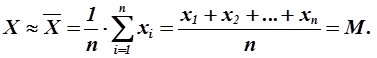(1.36)

Это равенство позволяет считать, что среднее арифметическое значение 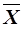(математическое ожидание M) является наиболее близким к истинному значению измеряемой величины X. Чем больше число измерений n тем больше М приближается к истинному значению.

Наиболее полно свойства случайной величины описываются функцией распределения. Она устанавливает связь между возможными значениями случайной погрешности и вероятностью появления этих значений. Распределение случайных погрешностей при практических расчетах чаще всего аппроксимируют нормальной функцией, т.е. наиболее часто на практике применяется нормальный закон распределения (распределение Гаусса).

Закон нормального распределения случайных погрешностей выражается следующей функцией распределения:

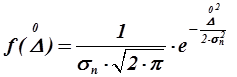, (1.37)

где 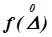– функция распределения плотности вероятностей случайной погрешности;

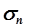– среднее квадратическое отклонение результата наблюдений при большом числе измерений (n→∞);

е = 2,7183 – основание натурального логарифма.

Графически закон распределения случайных погрешностей, выраженный уравнением (1.34), представляется в виде симметричной кривой, которую называют кривой нормального (Гауссовского) распределения случайных погрешностей (рис.1.15).

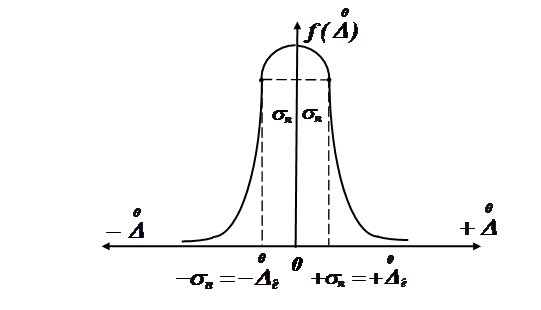
Рис. 1.15. Кривая нормального распределения

случайных погрешностей

Если через m_i обозначить частоту появления значения погрешности 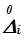при общем их числе n, то отношение 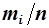, есть относительная частота появления значения .

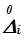При неограниченно большом числе наблюдений (n→∞) это отношение равнозначно понятию вероятности P_i, т.е. может рассматриваться как статистическая вероятность (P_i = 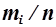) появления погрешности 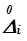при повторении измерений в неизменных условиях.

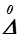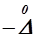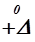Доверительная вероятность того, что погрешности не превосходят численно некоторого значения | |, т. е. лежат в пределах от до , может быть найдена (учитывая симметричность кривой нормального распределения) путем интегрирования уравнения (1.37):

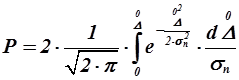. (1.38)

Произведя замену переменной 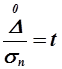, получим:

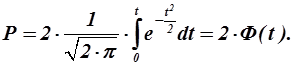(1.39)

Отсюда нормальная функция распределения

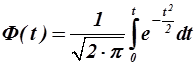(1.40)

Для облегчения расчетов для Ф(t) составлены таблицы для различных значений t (–0< t <–3,8; –3,8< t <3,8).

На кривой нормального распределения найдем точки перегиба и соответствующие им значения 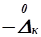и 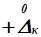. Для этого приравняем вторую производную уравнения (1.34) нулю и найдем, что перегиб кривой происходит в двух точках. Симметрично расположенных по обе стороны оси ординат 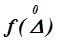при значениях 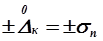. Точки перегиба разделяют области часто встречающихся случайных погрешностей от области редко встречающихся.

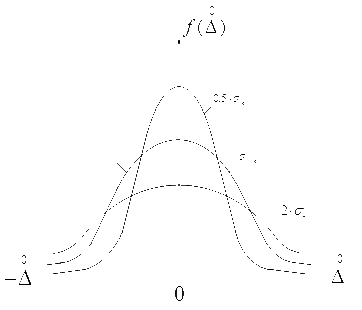
Рис. 1.16. Кривые нормального распределения погрешностей,
соответствующие трем различным значениям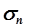

Для неограниченно большого ряда измерений 68,3% всех случайных погрешностей ряда лежит ниже данного значения 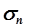и 31,7% выше его.

Параметр 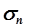однозначно характеризует форму кривой распределения случайных погрешностей. Ордината 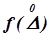кривой распределения, соответствующая 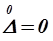обратно пропорциональна 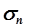. Площадь под кривой всегда равна 1. Следовательно, при увеличении 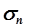получим кривую 3, при уменьшении – 1.

Конечная цель анализавыполненных измерений состоит в определение погрешности результата наблюдения для ряда значений измеряемой величины 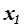, ,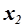…, 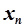и погрешности их среднего арифметического значения (т.е. результата измерения), принимаемого как окончательный результат измерения, с заданной вероятностью.