Езультаты суммирования в десятичной и двоично-десятичной системах счисления совпадают.
ример 1
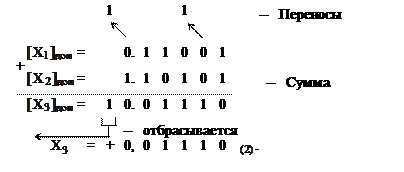 |
Выполним суммирование двух двоичных чисел X1 = + 0,11001 и X2 = – 0,01011 в дополнительном коде.
езультат получился положительным, и обратное преобразование не требуется.
ример 2
Поменяем знаки чисел  и
и  и выполним суммирование в дополнительном коде. Результат получится отрицательным, и потребуется обратное преобразование.
и выполним суммирование в дополнительном коде. Результат получится отрицательным, и потребуется обратное преобразование.

При сложении чисел одного знака может произойти переполнение разрядной сетки, что приведет к искажению результата. На практике для выявления переполнения разрядной сетки применяют модифицированные машинные коды, в которых два знаковых разряда. Для положительных чисел в знаковых разрядах записывается 00, для отрицательных – 11. Появление комбинаций 01 или 10 в знаковых разрядах свидетельствует о переполнении разрядной сетки, т.е. является сигналом ошибки. Например, двоичное число X = – 0,1101 в модифицированном дополнительном коде будет записано следующим образом:
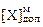 = 11.0011.
= 11.0011.
ример 3
Выполним суммирование двух десятичных чисел  = + 0,450 и
= + 0,450 и  = – 0,575 в двоичной СС с точностью до пяти знаков после запятой в дополнительном модифицированном коде и сравним результаты суммирования в двоичной и десятичной СС.
= – 0,575 в двоичной СС с точностью до пяти знаков после запятой в дополнительном модифицированном коде и сравним результаты суммирования в двоичной и десятичной СС.

Так как |  | > |
| > |  |, то в естественной форме следует выполнить вычитание числа X1 из числа X2 и результату присвоить знак минус.
|, то в естественной форме следует выполнить вычитание числа X1 из числа X2 и результату присвоить знак минус.
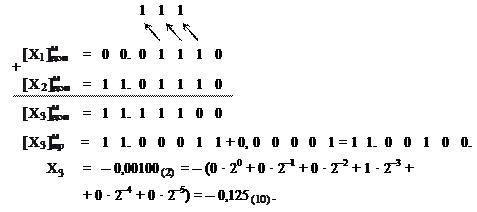
езультаты суммирования в естественной форме и дополнительном модифицированном коде совпадают.
Правило и пример перевода десятичного числа в двоично-десятичный код 8421 приведены в [1, С. 73, 74] и [5, С. 19, 20].
Рассмотрим пример:
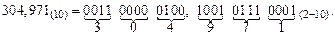
Правило и примеры суммирования десятичных чисел в коде 8421 приведены в [1, С. 85, 86], [2, С. 165], [3, С. 91, 92].
Рассмотрим пример суммирования десятичных чисел 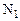 = 458 и
= 458 и 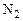 = 629 в десятичной СС и коде 8421.
= 629 в десятичной СС и коде 8421.
Десятичная система счисления:
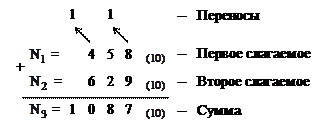
Код 8421:
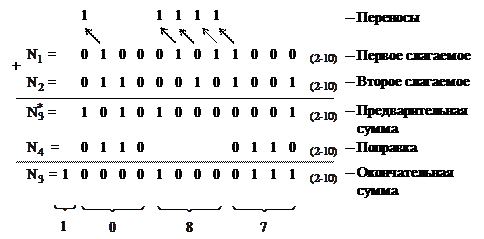
В младшей тетраде коррекция проведена из-за наличия единицы переноса во вторую тетраду.
езультаты суммирования в десятичной и двоично-десятичной системах счисления совпадают.
Задача 2
Разработайте логическую и принципиальную электрическую схему КЦУ, функционирование которого задано таблицей истинности (таблица 5).
1 Минимизируйте заданную логическую функцию табличным методом с помощью карт Карно. Запишите результат минимизации в МДНФ.
2 Постройте логическую схему устройства в базисе И, ИЛИ, НЕ.
3 Запишите результат минимизации через логическую операцию И-НЕ.
4 Постройте логическую схему устройства в базисе И-НЕ.
5 Постройте принципиальную электрическую схему устройства в базисе И-НЕ на микросхемах схемотехники КМОП, серия которых задана в примечании к таблице 5.
6 Проверьте правильность функционирования логических и принципиальной электрической схем КЦУ для пятого набора аргументов и сделайте вывод о правильности их функционирования.
7 Определите среднюю задержку распространения сигнала от входов к выходу и среднюю потребляемую мощность в принципиальной электрической схеме КЦУ.
Таблица 5 – Исходные данные к задаче 2
| Номер набора аргументов | Наборы аргументов | Номер варианта | |||||||||||||
| – | |||||||||||||||
| x1 | x2 | x3 | x4 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | |
| Ф | Ф | Ф | Ф | ||||||||||||
| Ф | Ф | Ф | Ф | ||||||||||||
| Ф | |||||||||||||||
| Ф | |||||||||||||||
| Ф | Ф | Ф | Ф | ||||||||||||
| Ф | Ф | Ф | |||||||||||||
| Ф | Ф | Ф | |||||||||||||
| Ф | |||||||||||||||
| Ф | Ф | Ф | Ф | Ф | |||||||||||
| Ф | |||||||||||||||
| Ф | Ф | Ф | Ф | ||||||||||||
| Ф | Ф | Ф | Ф | ||||||||||||
| Ф | Ф | ||||||||||||||
| Примечание – Для нечетных вариантов принципиальную электрическую схему КЦУ строить на микросхемах серии 1554, для четных – на микросхемах серии 1564 |
Методические указания по выполнению задачи 2
Предварительно изучите тему «Логические основы цифровой техники» по [1, С. 4-18], или [2, С. 38-52].
Рекомендуется следующая методика решения задачи 2.
1 Нанесите значения заданной логической функции на карту Карно и проведите минимизацию. Для построения логической схемы устройства в базисе И-НЕ результат минимизации запишите в минимальной дизъюнктивной нормальной форме (МДНФ). Для записи результата минимизации в МДНФ в замкнутые контуры (области) объединяйте клетки с единичными и неопределенными значениями ЛФ (Ф – неопределенное или факультативное значение ЛФ). При этом следует помнить, что в замкнутые области можно объединять одну, две, четыре, восемь и т.д. клеток. В результат минимизации входят только те аргументы, которые не меняют значение для всех клеток замкнутой области. Если значение аргумента равно 0, то его символ в МДНФ записывается со знаком отрицания.
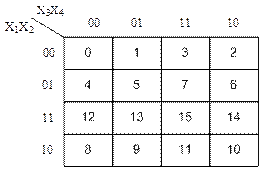
Рисунок 1 – Распределение наборов аргументов по клеткам карты Карно
2 Для построения логической схемы устройства в базисе И-НЕ результат минимизации необходимо сначала записать в базисе И, ИЛИ, НЕ в МДНФ, а затем полученную ЛФ преобразовать в базис И-НЕ.
3 Рассмотрим пример синтеза КЦУ в базисе И, ИЛИ, НЕ, функционирование которого задано таблицей истинности (f11(x1, x2, x3)) в таблице 4.
3.1 Нанесем значения логической функции f11(x1, x2, x3, x4) на карту Карно (рисунок 2) и проведем минимизацию, причем результат минимизации запишем в МДНФ.

Рисунок 2 – Карта Карно для минимизации логической функции в МДНФ
 (1)
(1)
3.2 Построим логическую схему устройства по выражению (1). Для этого потребуется:
- два логических элемента 2 И;
- один логический элемент 3 ИЛИ;
- три логических элемента 3 НЕ.
Логическая схема устройства в базисе И, ИЛИ, НЕ, построенная по логической функции (1), представлена на рисунке 3.
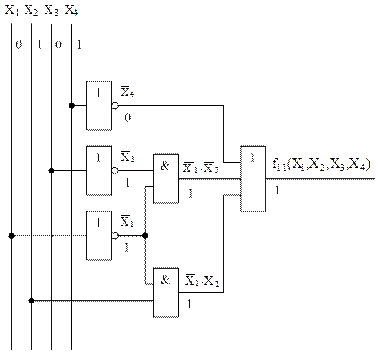
Рисунок 3 – Логическая схема устройства в базисе И, ИЛИ, НЕ в МДНФ
4 Рассмотрим пример синтеза КЦУ в базисе И-НЕ для той же ЛФ.
4.1 Преобразуем ЛФ (1) в базис И-НЕ, используя правило де Моргана:

|
4.2 Построим логическую схему устройства в базисе И-НЕ по выражению (3), при этом одиночные отрицания аргументов реализуем на основе ЛЭ 2 И-НЕ с объединенными входами. Для этого необходимо использовать:
- четыре логических элемента 2 И-НЕ;
- один логический элемент 3 И-НЕ.
Логическая схема устройства в базисе И-НЕ представлена на рисунке 4.
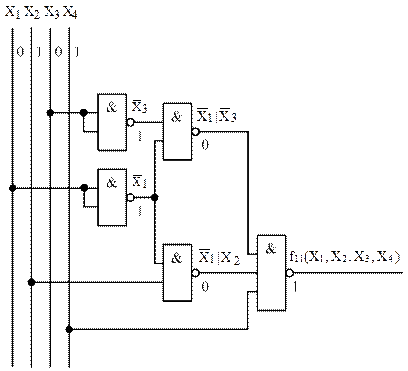
Рисунок 4 – Логическая схема устройства в базисе И-НЕ
4.3 Построим принципиальную электрическую схему устройства в базисе И-НЕ на микросхемах стандартной логики схемотехники КМОП серии 1554. Для этого по приложениям Б и В выбираем стандартные микросхемы интегральных ЛЭ серии 1554 и соединяем их между собой в соответствии с логической схемой на рисунке 4. Выбираем микросхему ЭКР1554ЛА3 (IN74AC00N), в одном корпусе которой выполнено четыре ЛЭ 2 И-НЕ, а также ЭКР1554ЛА4 (IN74AC10N) – три ЛЭ 3 И-НЕ (два останутся свободными). Принципиальная электрическая схема устройства в базисе И-НЕ представлена на рисунке 5. На схеме указаны буквенно-позиционные обозначения микросхем по ГОСТ 2.710-81, номера выводов, а также уровни сигналов для пятого набора аргументов (уровни сигналов указаны под линиями выводов микросхем).
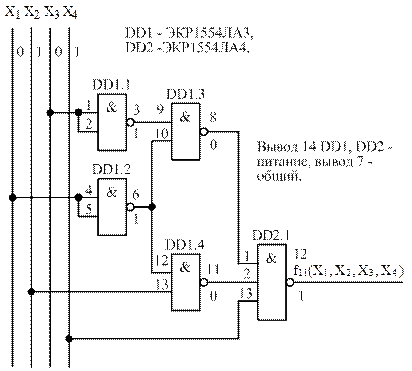
Рисунок 5 – Принципиальная электрическая схема устройства в базисе И-НЕ
4.4 Определим среднюю задержку распространения сигнала от входа к выходу устройства и среднюю потребляемую мощность.
В худшем случаем сигнал передается через три ЛЭ. Для расчета средней задержки возьмем данные из приложения Б. В результате получаем суммарную среднюю задержку распространения сигнала от входа к выходу устройства  нс.
нс.
Для расчета средней потребляемой мощности всей схемы необходимо расчетным путем определить среднюю потребляемую мощность каждой микросхемы путем умножения среднего потребляемого тока ( см. [7], приложение Б ) на напряжение источника питания. В результате получаем суммарную среднюю потребляемую мощность  мкВт.
мкВт.
5 Проверим правильность функционирования логических и принципиальной схем КЦУ (рисунки 3...5). Для этого проставим на выходах всех логических элементов значения сигналов для пятого набора аргументов. Поскольку на выходах схем единичный уровень сигнала, то они функционируют в соответствии с таблицей истинности (см. значение логической функции 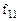 для пятого набора аргументов).
для пятого набора аргументов).
Задача 3
Разработайте логическую схему КЦУ, заданного в таблице 6.
Таблица 6 – Исходные данные к задаче 3
| Номер варианта | Наименование КЦУ | Базис |
| Преобразователь кода 8421 в код «с избытком 3» | И-НЕ | |
| Мультиплексор на восемь входов без стробирования | И-ИЛИ-НЕ | |
| Дешифратор кода 2421 на десять выходов со стробированием | И-НЕ | |
| Шифратор для преобразования десятичных цифр в код «с избытком 3» со стробированием | И, ИЛИ, НЕ | |
| Дешифратор кода 7421 на десять выходов со стробированием | И-НЕ | |
| Преобразователь кода 7421 в код 2421 | И-НЕ | |
| Шифратор для преобразования десятичных цифр в код 7421 со стробированием | И, ИЛИ, НЕ | |
| Мультиплексор на восемь входов со стробированием | И-ИЛИ-НЕ | |
| Дешифратор кода «с избытком 3» на десять выходов со стробированием | И-НЕ | |
| Преобразователь кода «с избытком 3» в код 8421 | И-НЕ |
1 Дайте определение и поясните назначение заданного КЦУ.
2 Приведите его условное графическое обозначение и поясните назначение выводов.
3 Составьте таблицу истинности для заданного КЦУ.
4 Запишите логические функции для выходов заданного КЦУ в базисе И, ИЛИ, НЕ (для преобразователей кодов логические функции минимизировать табличным методом с помощью карт Карно).
5 Запишите полученные логические функции в базисе, заданном в таблице 6.
6 Постройте логическую схему КЦУ в базисе, заданном в таблице 6.
7 Проверьте правильность функционирования построенной логической схемы КЦУ для четвертой строки таблицы истинности.
Методические указания по выполнению задачи 3
В задаче 3 рассматриваются следующие типовые КЦУ: преобразователи кодов, мультиплексоры, шифраторы и дешифраторы.
В вариантах 1,6 и 10 задачи 3 требуется синтезировать в базисе И-НЕ схемы преобразователей кодов. В учебниках [1, С. 117-120] и [2, С. 188-190] приведены примеры синтеза преобразователя кода 8421 в код 2421 и обратно. Причем минимизация логических функций выполнена табличным методом с помощью карт Вейча. Рассмотрим пример синтеза преобразователя кода 8421 в код 2421 при минимизации логических функций с помощью карт Карно, которые более удобны и нашли более широкое практическое применение. Условное графическое обозначение такого преобразователя кода представлено на рисунке 6.

Рисунок 6 – Условное графическое обозначение преобразователя кода 8421 в код 2421
Закон функционирования преобразователя кода представлен в таблице 7.
Таблица 7 – Таблица истинности преобразователя кода 8421 в код 2421
| Десятичное число | Код 8421 | Код 2421 | ||||||
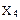 | 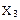 | 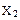 | 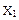 |  | 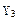 | 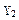 | 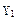 | |
На основании таблицы истинности преобразователя кодов заполним карты Карно (рисунок 7) и запишем логические функции для выходов 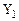 ,…,
,…, 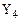 в МДНФ.
в МДНФ.

Рисунок 7 – Карты Карно для преобразователя кода 8421 в код 2421
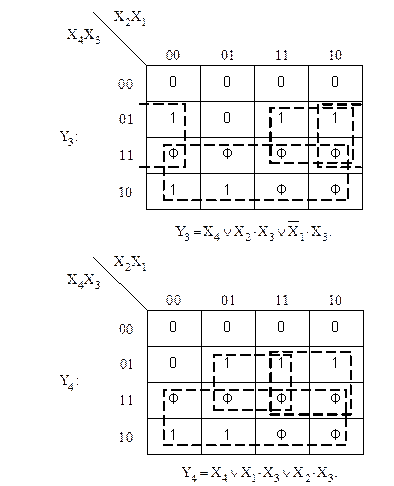
Окончание рисунка 7
 (3)
(3)
Преобразуем логические функции (3) в базис И-НЕ, используя правило де Моргана.
|
 (4)
(4) Логическая схема преобразователя кода 8421 в код 2421 в базисе И-НЕ, построенная по логическим функциям (4), представлена на рисунке 8.
Для проверки правильности функционирования логической схемы преобразователя кода проставим на выходах логических элементов значения сигналов для входного кодового слова 0011. Поскольку на выходах схемы устанавливается кодовое слово 0011, то преобразователь кода функционирует в соответствии с таблицей истинности.
Следует помнить, что проверка правильности функционирования только по одному входному набору является неполной.
Методика синтеза преобразователей кодов, заданных в вариантах 1, 6 и 10, аналогична. Для составления таблицы истинности следует использовать данные таблицы 8.
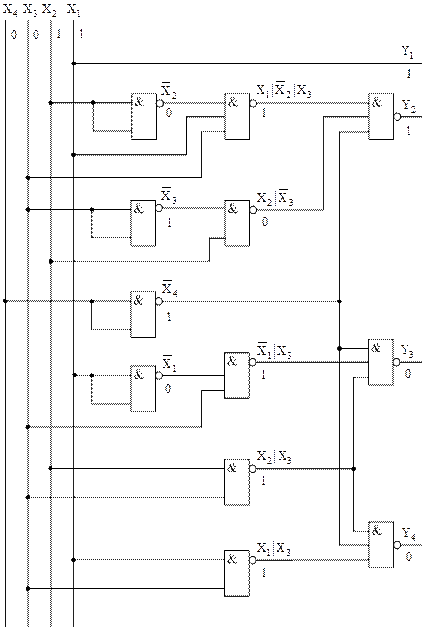
Рисунок 8 – Логическая схема преобразователя кода 8421 в код 2421 в базисе И-НЕ
Таблица 8 – Двоично-десятичные коды
| Десятичное число | Двоично-десятичные коды | |||
| «с избытком 3» | ||||
| Примечание – Код «с избытком 3» часто называют кодом 8421+3 |
В вариантах 2 и 8 задачи 3 требуется синтезировать в базисе И-ИЛИ-НЕ схему мультиплексора на восемь каналов (мультиплексоры называют коммутаторами каналов). Рассмотрим пример синтеза мультиплексора на четыре канала со стробированием. Условное графическое обозначение мультиплексора и назначение выводов представлено в [1, С. 123-125] и [3, С. 141-144]. Таблица истинности мультиплексора представлена в таблице 9.
Таблица 9 – Таблица истинности мультиплексора на четыре канала со стробированием
| Адресные входы | Стробирующий сигнал | Выход | |
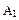 |  | 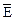 | Q |
| X | X | ||
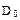 | |||
 | |||
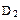 | |||
 | |||
| Примечание – Знаком «X» обозначен произвольный уровень сигнала – 0 или 1 |
Из таблицы истинности следует, что при отсутствии стробирующего (разрешающего) сигнала ( 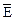 =1) на выходе мультиплексора Q устанавливается нулевой сигнал независимо от кода на адресных входах
=1) на выходе мультиплексора Q устанавливается нулевой сигнал независимо от кода на адресных входах 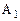 ,
, 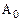 . При поступлении стробирующего сигнала (
. При поступлении стробирующего сигнала ( 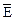 =0) на выход мультиплексора Q передается сигнал с того информационного входа
=0) на выход мультиплексора Q передается сигнал с того информационного входа 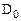 …
…  , номер которого указан на адресных входах
, номер которого указан на адресных входах 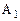 ,
, 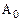 .
.
На основании таблицы истинности мультиплексора запишем логическую функцию для выхода Q в совершенной дизъюнктивной нормальной форме (СДНФ):
 (5)
(5)
По логической функции (5) можно построить логическую схему мультиплексора в базисе И, ИЛИ, НЕ, однако, более простой логическая схема мультиплексора будет в базисе И-ИЛИ-НЕ. Для преобразования логической функции (5) в базис И-ИЛИ-НЕ следует проинвертировать левую и правую части равенства:
 (6)
(6)
Из логической функции (6) следует, что в базисе И-ИЛИ-НЕ мультиплексор будет иметь инверсный выход, поэтому для получения прямого выхода к его выходу следует подключить инвертор.
Логическая схема мультиплексора в базисе И-ИЛИ-НЕ, построенная по логической функции (6), представлена на рисунке 9.
Для проверки правильности функционирования логической схемы мультиплексора проставим значения сигналов для адресного кода 11. Поскольку на выход схемы Q передается сигнал со входа D3, то мультиплексор функционирует в соответствии с таблицей истинности.
Синтез мультиплексора, заданного в вариантах 2 и 8, следует выполнять по вышеприведенной методике.
В вариантах 3, 5 и 9 задачи 3 требуется синтезировать схему дешифратора в базисе И-НЕ со стробированием, т.е. с разрешающим входом 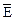 .
.

Рисунок 9 – Логическая схема мультиплексора в базисе И-ИЛИ-НЕ
Условное графическое обозначение дешифратора с инверсными выходами представлено на рисунке 10.
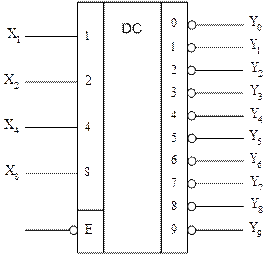
Рисунок 10 – Условное графическое обозначение дешифратора кода 8421 на десять выходов в базисе И-НЕ со стробированием
В дешифраторах с инверсными выходами активным уровнем сигнала на выходах является уровень логического нуля.
Таблица истинности дешифратора представлена в таблице 10.
Таблица 10 – Таблица истинности дешифратора кода 8421 на десять выходов со стробированием
| Входной код 8421 | Строб (разрешение) | Выходные сигналы | ||||||||||||
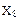 | 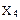 | 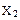 | 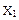 | 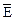 | 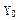 | 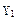 | 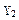 | 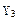 |  | 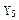 |  |  |  | 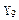 |
| X | X | X | X | |||||||||||
Из таблицы истинности следует, что дешифратор преобразует входной код в сигнал активного уровня на одном из выходов, если на стробирующем входе активный уровень сигнала ( 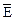 = 0). В противном случае на всех выходах дешифратора устанавливаются пассивные уровни сигнала (единичные).
= 0). В противном случае на всех выходах дешифратора устанавливаются пассивные уровни сигнала (единичные).
По данным таблицы 10 запишем логические функции для выходов дешифратора в СКНФ:
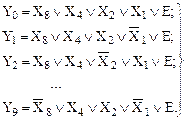 (7)
(7)
Преобразуем логические функции (7) в базис И-НЕ, используя закон двойного отрицания и правило де Моргана:
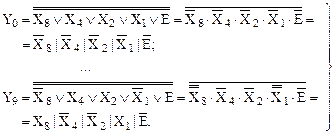 (8)
(8)
Логическая схема дешифратора в базисе И-НЕ, построенная по логическим функциям (8), представлена на рисунке 11.
Следует помнить, что в дешифраторах с прямыми выходами активным уровнем сигнала на выходах является уровень логической единицы и логические функции следует записывать в СДНФ.
Поскольку на рисунке 11 представлена упрощенная логическая схема дешифратора, то проверку правильности ее функционирования выполним не для четвертой, а для десятой строки таблицы истинности. Так как активный уровень сигнала устанавливается на выходе 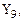 то схема дешифратора функционирует в соответствии с таблицей истинности.
то схема дешифратора функционирует в соответствии с таблицей истинности.
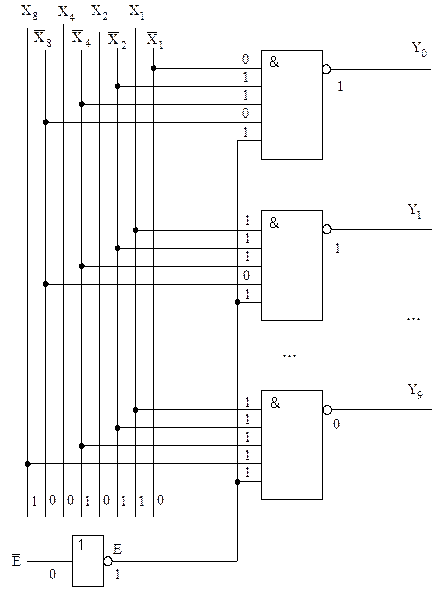
Рисунок 11 – Логическая схема дешифратора кода 8421 на десять выходов в базисе И-НЕ со стробированием
Синтез логической схемы дешифратора, заданного в вариантах 3, 5 и 9, следует выполнять по вышеприведенной методике. При составлении таблицы истинности заданного дешифратора используются данные таблицы 8. Логические функции записываются для всех выходов дешифратора, и строится полная логическая схема.
В вариантах 4 и 7 задачи 3 требуется синтезировать схему шифратора. В учебниках [1, С. 110-112] и [2, С. 181-184] показан пример синтеза двоичного шифратора десятичных цифр от 0 до 9 в код 8421 без стробирования. Рассмотрим пример синтеза шифратора десятичных цифр от 0 до 9 в код 8421 со стробированием.
Условное графическое обозначение шифратора для преобразования десятичных цифр от 0 до 9 в код 8421 с разрешающим (стробирующим) входом представлено на рисунке 12.
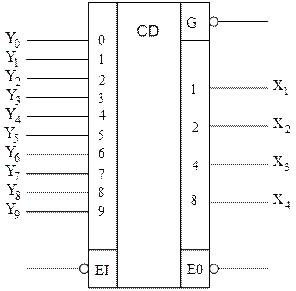
Рисунок 12 – Условное графическое обозначение шифратора для преобразования десятичных цифр от 0 до 9 в код 8421
Сигналы, соответствующие десятичным цифрам, подаются на входы  ,
, 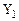 ,…,
,…, 
Нулевое значение сигнала на разрешающем (стробирующем) входе  разрешает работу данного шифратора. Нулевое значение сигнала на выходе
разрешает работу данного шифратора. Нулевое значение сигнала на выходе  отмечает наличие возбужденного входа у данного шифратора.
отмечает наличие возбужденного входа у данного шифратора.
Чтобы выделить ситуацию, когда отсутствуют возбужденные входы, в данном шифраторе имеется дополнительный выход 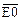 (разрешение по выходу). Нулевое значение сигнала на выходе
(разрешение по выходу). Нулевое значение сигнала на выходе 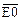 вырабатывается при отсутствии возбужденных входов у данного шифратора для разрешения работы следующего (младшего) шифратора при наращивании числа входов и выходов.
вырабатывается при отсутствии возбужденных входов у данного шифратора для разрешения работы следующего (младшего) шифратора при наращивании числа входов и выходов.
На выходах 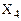 –
–  формируется выходное кодовое слово.
формируется выходное кодовое слово.
Таблица истинности, описывающая функционирование данного шифратора, представлена в таблице 11.
Таблица 11 – Таблица истинности шифратора для преобразования десятичных цифр от 0 до 9 в код 8421
| Входные сигналы | Выходные сигналы | |||||||||||||||
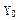 | 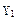 | 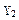 | 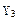 |  | 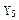 |  |  |  | 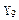 |  | 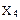 | 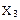 | 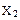 | 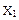 |  | 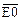 |
| X | X | X | X | X | X | X | X | X | X | |||||||
Как видно из таблицы истинности, все вышеперечисленные сигналы на выходах шифратора формируются при наличии активного уровня сигнала на входе разрешения (  = 0). При пассивном уровне сигнала на входе разрешения (
= 0). При пассивном уровне сигнала на входе разрешения (  = 1) независимо от состояния информационных входов шифратора на информационных выходах формируется кодовое слово 0000 и пассивные уровни сигналов на выходах
= 1) независимо от состояния информационных входов шифратора на информационных выходах формируется кодовое слово 0000 и пассивные уровни сигналов на выходах  и
и 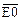 .
.
При отсутствии возбужденных входов (вторая строка в таблице истинности) на выходе 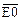 формируется активный уровень сигнала (
формируется активный уровень сигнала ( 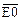 = 0).
= 0).
По данным таблицы 11 запишем логические функции для информационных выходов шифратора. Каждая из них представляет дизъюнкцию входных аргументов  (i = 0, 1, … , 9), для которых значение функции равно 1.
(i = 0, 1, … , 9), для которых значение функции равно 1.
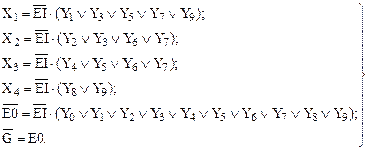 (9)
(9)
Из таблицы истинности очевидно, что логическая функция для выхода  является инверсией логической функции для выхода
является инверсией логической функции для выхода 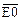 .
.
Логическая схема шифратора в базисе И, ИЛИ НЕ, построенная по логическим функциям (9), представлена на рисунке 13.
Для проверки правильности функционирования логической схемы шифратора подадим на ее входы сигналы, соответствующие четвертой строке таблицы истинности ( 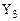 = 1). Так как на выходах устанавливается кодовое слово 0011, а так же
= 1). Так как на выходах устанавливается кодовое слово 0011, а так же  = 0,
= 0, 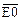 = 1, то логическая схема шифратора функционирует в соответствии с таблицей истинности.
= 1, то логическая схема шифратора функционирует в соответствии с таблицей истинности.
Синтез логической схемы шифратора, заданного в вариантах 4 и 7, следует выполнять по вышеприведенной методике. При составлении таблицы истинности в качестве выходного кода 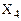 ,
, 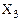 ,
,  ,
,  использовать данные таблицы 8.
использовать данные таблицы 8.

Рисунок 13 – Логическая схема шифратора для преобразования десятичных цифр от 0 до 9 в код 8421 в базисе И, ИЛИ, НЕ со стробированием
Задача 4
Изучите микросхему КЦУ схемотехники КМОП, заданную в таблице 12.
Таблица 12 – Исходные данные к задаче 3
| Номер варианта | Условное обозначение ИМС | Код на входах | Номер выхода | |
| международное | прототип | |||
| Дешифраторы-демультиплексоры | ||||
| IN74AC137N | ЭКР1554ИД7 | Y3 | ||
| IN74HC154AN | ЭКР1564ИД3 | Y7 | ||
| IN74ACT139N | ЭКР1594ИД14 | Y3 | ||
| IN74HCT138AN | ЭКР5564ИД7 | Y4 | ||
| IN74HC139AN | ЭКР1564ИД14 | Y1 | ||
| Мультиплексоры | ||||
| IN74AC157N | ЭКР1554КП16 | B0…B3 | ||
| IN74HC158AN | ЭКР1564КП18 |  | ||
| IN74ACT251N | ЭКР1594КП15 | D6 | ||
| IN74AC253N | ЭКР1554КП12 | D1 | ||
| IN74HCT251AN | ЭКР5564КП15 | D4 |
1 Дайте определение и поясните назначение заданного КЦУ.
2 Зарисуйте по [7, приложение В], условное графической обозначение (УГО) заданной микросхемы и поясните назначение выводов.
3 Зарисуйте по [7, приложение В], таблицу истинности для заданной микросхемы и поясните принцип работы.
4 Укажите, какой выход дешифратора-демультиплексора будет выбран, если на информационных входах действует код, заданный в таблице 12. Поясните, при каком условии активный уровень сигнала появится на выбранном выходе и какой уровень сигнала будет на остальных выходах (выполняется для вариантов 1-5).
5 Укажите код, который поступает на информационные и разрешающие входы дешифратора-демультиплексора, если выбран указанный в таблице 12 выход (выполняется для вариантов 1-5).
6 Укажите, какой информационный вход будет соединяться с выходом мультиплексора, если на адресных входах действует код, заданный в таблице 12 (выполняется для вариантов 6-10).
7 Укажите код, который необходимо подать на адресные и разрешающий входы микросхемы мультиплексора, чтобы с выходом соединялся вход, указанный в таблице 12 (выполняется для вариантов 6-10).
8 Определите по [7, приложение Б] основные электрические параметры заданной микросхемы КЦУ. Результат запишите в таблицу, аналогичную по форме таблице 13.
Методические указания по выполнению задачи 4
В задаче 4 необходимо изучить стандартную микросхему КЦУ схемотехники КМОП. Для решения этой задачи следует использовать справочный материал, приведенный в [7, приложения Б и В].
| Таблица 13 – Основные статические и динамические параметры заданных микросхем (образец заполнения) |  (tPHL), не более (tPHL), не более | нс | Примечания 1 В скобках указаны международные обозначения соответствующих параметров. 2   Параметры указаны для напряжения источника питания UИП = 5 В и рабочей температуры от минус 40 до плюс 85°С. Максимальный потребляемый ток Iпот указан для выходного тока = 0 мкА, а уровни выходных напряжений и – для ≤ 50 мкА. Параметры указаны для напряжения источника питания UИП = 5 В и рабочей температуры от минус 40 до плюс 85°С. Максимальный потребляемый ток Iпот указан для выходного тока = 0 мкА, а уровни выходных напряжений и – для ≤ 50 мкА. | ||
 (tPLH), не более (tPLH), не более | нс | ||||
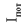 (ICC), не более (ICC), не более | мкА | ||||
 (IOH), не более (IOH), не более | мА | – 4 | – 24 | ||
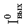 (IOL), не более (IOL), не более | мА | ||||
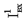 (IIH), не более (IIH), не более | мкА | 1,0 | 1,0 | ||
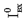 (IIL), не более (IIL), не более | мкА | – 1,0 | – 1,0 | ||
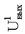 (VOH), не менее (VOH), не менее | В | 4,9 | 4,9 | ||
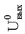 (VOL), не более (VOL), не более | В | 0,1 | 0,1 | ||
| UИП (VCC) | В | ||||
| Схемо-техника | КМОП | КМОП | |||
| Условное обозначение по ГОСТ 17021-88 (прототип) | ЭКР1564ЛИ6 | ЭКР1554ЛА1 | |||
| Международное обозначение микросхем | IN74HC21AN | IN74AC20N |
ЛИТЕРАТУРА
1 Калабеков, Б. А. Цифровые устройства и микропроцессорные системы : учеб. для техникумов связи / Б. А. Калабеков. – М. : Горячая линия – Телеком, 2002. – 336 с.
2 Калабеков, Б. А. Цифровые устройства и микропроцессорные системы : учеб. для техникумов связи / Б. А. Калабеков, И. А. Мамзелев. – М. : Радио и связь, 1987. – 400 с.
3 Лысиков, Б. Г. Цифровая и вычислительная техника : учеб. для техникумов связи / Б. Г. Лысиков. – Мн. : УП Экоперспектива, 2002. – 264 с.
4 Угрюмов, Е. П. Цифровая схемотехника : учеб. пособие для вузов / Е. П. Угрюмов. – Спб. : БХВ-Петербург, 2002. – 582 с.
5 Цифровые интегральные микросхемы : справочник, 2-е изд., перераб. и доп. / М. И. Богданович [и др.]. – Мн. : Беларусь, Полымя, 1996. – 605 с.
6 Цифровые и микропроцессорные устройства : конспект лекций для студентов специальностей 2-45 01 03 – Сети телекоммуникаций, 2‑45 01 02 – Системы радиосвязи, радиовещания и телевидения. В 5 ч. Ч. 4 : Основы микропроцессорной техники; Ч. 5 : Принципы организации однокристальных микроконтроллеров. Организация памяти микропроцессорных систем / сост. В. И. Богородов. – Минск : ВГКС, 2009. – Ч. 4 – 63 с.; Ч. 5 – 85 с.
7 Цифровые и микропроцессорные устройства : лабораторный практикум для студентов специальностей 2-45 01 03 – Сети телекоммуникаций, 2‑45 01 02 – Системы радиосвязи, радиовещания и телевидения. В 4 ч. / сост. В. И. Богородов. – Минск : ВГКС, 2009. – Ч. 1 – 84 с.; Ч. 2 – 65 с.
СОДЕРЖАНИЕ
Введение. 3
Контрольные задания. 5
Задача 1. 5
Методические указания по выполнению задачи 1. 6
Задача 2. 13
Методические указания по выполнению задачи 2. 14
Задача 3. 20
Методические указания по выполнению задачи 3. 21
Задача 4. 37
Методические указания по выполнению задачи 4. 38
Литература. 40
Учебное издание
ЦИФРОВЫЕ И МИКРОПРОЦЕССОРНЫЕ УСТРОЙСТВА
Программа, методические указания и контрольные задания
для учащихся заочной формы обучения специальностей
2-45 01 33 – Сети телекоммуникаций
2-45 01 32 – Системы радиосвязи, радиовещания и телевидения
Составитель
Богородов Владимир Ильич
Редактор Е. Б. Левенкова
Компьютерная верстка И. А. Крутая
План 2009/2010 уч.г., поз. 54
Подписано в печать 14.09.2009. Формат 60*84/16.
Бумага офсетная. Гарнитура «Times».
Печать цифровая.
Усл. печ. л. ___. Уч.-изд. л. ___.
Тираж ___ экз. Заказ ___.
Издатель и полиграфическое исполнение:
учреждение образования
«Высший государственный колледж связи»
ЛИ № 02330/0131902 от 03.01.2007.
 Ул. Ф. Скорины, 8/2, 220114, Минск
Ул. Ф. Скорины, 8/2, 220114, Минск
