Нечеткая импликация
Пусть имеем обычные («четкие») высказывания вида: p = «x есть A» и q = «y есть B». Тогда импликацией (в обычной, «четкой» логике) «если p, то q» называется предложение, которое ложно тогда и только тогда, когда p истинно, а q ложно.
Такой вид отношений между высказываниями обычно обозначается как 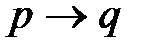 и понимается как утверждение «p влечет за собой q».
и понимается как утверждение «p влечет за собой q».
Если перейти к бинарной (булевой) алгебре логики, где с понятием «истина» сопоставляется 1, а с понятием «ложь» - 0, то импликацию можно представить логической формулой
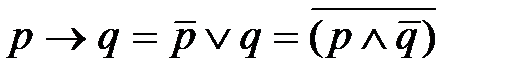 ,
,
или таблицей истинности:
| p | q | 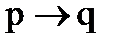 |
Более полная трактовка понятия импликации означает, что истинность 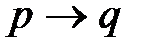 - это тоже, что истинность утверждения «степень истинности q не меньше, чем степень истинности p», т.е.
- это тоже, что истинность утверждения «степень истинности q не меньше, чем степень истинности p», т.е.
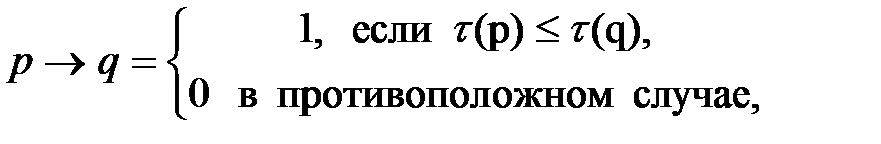
где - 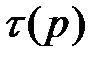 и
и 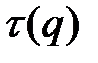 - указанные «степени истинности» (в четкой логике принимающие значения лишь 0 или 1).
- указанные «степени истинности» (в четкой логике принимающие значения лишь 0 или 1).
Пример - 18. Пусть p = «x больше 5» и q = «x больше 4». Легко видеть, что в данном случае импликация 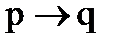 является истинной, поскольку из неравенства x>5 следует неравенство x>4.
является истинной, поскольку из неравенства x>5 следует неравенство x>4.
Нечеткая импликация, в принципе сохраняет тот же смысл, что и импликация четкой логики. Отличие состоит лишь в том, что в этом случае «степени истинности» могут иметь любое значение между 0 и 1.
Нечеткая импликация определяется обычно следующим образом.
Будем считать, что заданы универсальные множества X и Y, содержащие конечное число элементов. Под способом определения нечеткой импликации «если А, то В», где А и В - нечеткие множества на X и Y соответственно (например: «если температура - большая, то скорость близка к нулю»), будем понимать способ задания нечеткого отношения R на X´Y, соответствующего данному высказыванию.
Такое отношение можно задать по-разному, поэтому для математического представления нечеткой импликации предложено большое число различных формул, некоторые из которых вместе с фамилиями предложивших их авторов приведены ниже [18]:
Ларсен (Larsen): 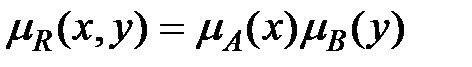 .
.
Лукасевич (Lukasiewicz): 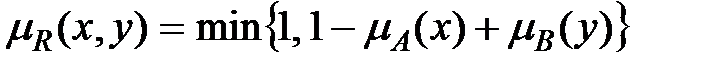 .
.
Мамдани (Mamdani): 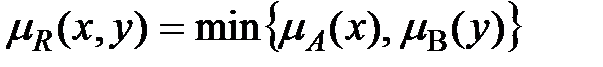 .
.
Брауэра: 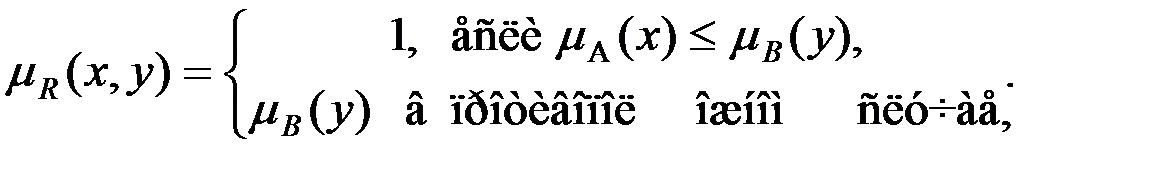
Гёдель (классическая нечеткая импликация):
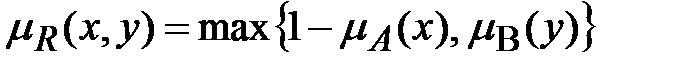 .
.
В общем, какого-либо преимущества одной формулы над другими нет, поэтому все они (а к настоящему времени известно несколько десятков подобных формул) имеют право на существование.

8.Нечетко-логические экспертные системы: обобщенная структурная схема, назначение отдельных модулей, пример функционирования.
