Погрешности измерений

Никакое измерение не может быть выполнено абсолютно точно. В результатах измерений всегда присутствуют ошибки. Погрешностью называют отклонение результата измерений Х от действительного (истинного) значения измеряемой величины Q. D=X-Q. Погрешность указывает границы неопределенности значения измеряемой величины.

Истинное значение ФВ считается неизвестным и применяется только в теоретических исследованиях. Действительное значение ФВ устанавливается экспериментальным путем в предположении, что результат измерения в максимальной степени приближается к истинному значению, тогда результат измерения будет представлять собой приближенную оценку истинного значения величины, найденную путем измерения.

По характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и грубые (промахи); по отношению к условиям применения - основные и дополнительные; по отношению к измеряемой величине - динамические и статистические; по способу выражения - абсолютные, относительные и приведенные; по способу суммирования - аддитивные и мультипликативные.

Случайная погрешность - является составляющей погрешности измерения, изменяющейся случайным образом (по знаку и значению) в серии проводимых измерений одного и того же размера ФВ, проведенных с одинаковой тщательностью в одних и тех же условиях. Погрешность не имеет закономерностей, она не устранима, избежать ее невозможно, она всегда присутствует в результатах измерений. Случайные погрешности не устраняются путем введения поправок.

Грубая погрешность (промах) - это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Они, как правило, возникают из-за ошибок оператора, или кратковременных резких ухудшений условий проведения измерений. Промахи легко обнаруживаются в ряде измерений и их результаты отбрасываются.

Рассеяние результатов в ряду измерений - несовпадение результатов одной и той же величины в ряду равноточных измерений, как правило, обусловлено действием случайных погрешностей при измерении и носит вероятностный характер. Оценками рассеяния результатов в ряду равноточных измерений одной и той же ФВ могут быть:

1. Размах результатов измерений вычисляется по формуле: 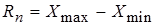где n - объем выборки.

2. Средняя квадратическая погрешность результатов измерений (СКП)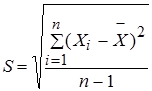

На практике широко распространен термин среднее квадратическое отклонение (СКО) - отклонение результатов в ряду измерений от их среднего арифметического значения. В метрологии это отклонение называют погрешностью измерений, поэтому в соответствии с РМГ 29-99 целесообразно применять термин СКП. При обработке ряда результатов, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов измерений.

3. Средняя квадратическая погрешность среднего арифметического вычисляется по формуле:

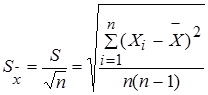где S – СКП, n – объем выборки, число измерений в ряду.

4. Доверительные границы погрешности результата измерений - наибольшее и наименьшее значения погрешностей измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится истинное (искомое) значение погрешности результата измерений.

Предельная погрешность измерения - максимальная погрешность (+,-), допускаемая для данной измерительной задачи. Во многих случаях за предельную погрешность принимают величину 3S, т.е.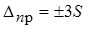

Систематическая погрешность - составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же ФВ. В зависимости от характера измерения систематические погрешности подразделяются на: постоянные, прогрессирующие, периодические и погрешности, изменяющиеся по сложному закону. Приведенная классификация является условной, так как не всегда можно провести четкие границы между названными группами.

Постоянные погрешности - погрешности, которые длительное время сохраняют свое значение, например, в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто. К постоянным погрешностям относятся погрешности большинства мер, например, гирь, магазинов сопротивлений и др., а также погрешности градуировки шкал измерительных приборов.

Прогрессивные погрешности - непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля. Одной из причин их возникновения может быть постепенное падение напряжения источника тока, питающего измерительную цепь. Например, аккумуляторы во время работы вначале разряжаются быстро, затем медленно, равномерно в течение длительного времени, а затем, в конце процесс, ускоряется и сопровождается сильным снижением напряжения.

Периодические погрешности - погрешности, значение которых являются периодической функцией времени или перемещения указателя измерительного прибора, т.е. это погрешности, периодически изменяющие значение и знак. Периодическая погрешность чаще всего возникает при использовании СИ с круговой шкалой, стрелка которых при измерении совершает несколько оборотов (н-р, секундомер). Периодическая погрешность возникает в тех случаях, когда ось вращения стрелки не совпадает с центром окружности шкалы (смещена вниз по отношению к центру). При вертикальном положении стрелки это смещение погрешности не вызывает.

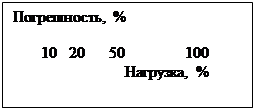Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей. Одним из примеров являются погрешности электрических счетчиков, зависимость которых от нагрузки (потребляемой мощность) выражается кривой.

Систематические погрешности могут быть предсказаны и благодаря этому устранены путем введения соответствующих поправок. Одним из способов обнаружения и устранения этих погрешностей является поверка прибора (аттестация по образцовым мерам или сигналам).

Субъективная (личная) погрешность измерения - составляющая систематической погрешности измерения, обусловленная индивидуальными особенностями оператора т.е. погрешностью отсчета оператором показаний по шкалам СИ, диаграммам регистрирующих приборов. Они вызываются состоянием оператора, его положением во время работы, несовершенством органов чувств. В возникновении субъективных погрешностей большую роль играет скорость реакции на полученный сигнал.

Неисключенная систематическая погрешность (НСП) - составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введением поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости. НСП характеризуется границами, которые вычисляются по формулам:

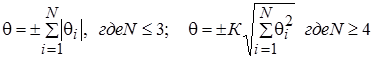
Суммарная средняя квадратическая погрешность (суммарная погрешность результата, суммарная погрешность) - погрешность результата измерений состоящая из суммы случайных и неисключенных систематических погрешностей принимаемых за случайные, вычисляются по формул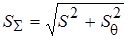е: где 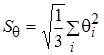- средняя квадратическая погрешность суммы неисключенных систематических погрешностей при равномерном распределении.

Прогрессирующая погрешность (дрейфовая) - это непредсказуемая погрешность, медленно меняющаяся во времени. Эти погрешности требуют непрерывного повторения и коррекции, так как могут быть скорректированы введением поправки лишь в данный момент времени, а далее вновь непредсказуемо возрастают. Другая их особенность состоит в том, что их изменение во времени представляет собой нестационарный случайный процесс. По природе своей эти погрешности определяются процессом старения тех или иных деталей и узлов аппаратуры.

По способу выражения погрешности делятся на абсолютную, относительную, приведенную.

Абсолютная погрешность измерения выражается в единицах измеряемой величины и определяется как разность D = X-Q (D = X-Х_и; или D = X-Х_д) где Х – результат измерений, Q истинное значение. Абсолютная погрешность не может сама по себе служить показателем точности измерений, так как одно и тоже ее значение, например D = 0,01 мм при Х = 100 мм, соответствует достаточно высокой точности, а при Х = 0,5 мм - достаточно низкой точности.

По зависимости абсолютной погрешности от значений измеряемой величины различают аддитивные и мультипликативные погрешности.

Аддитивная погрешность или погрешность нуля - абсолютная погрешность, постоянная во всем диапазоне измерений, то есть не зависит от измеряемой величины, может являться следствием неточной установки на нуль стрелки приборов перед измерением.

Мультипликативная погрешность или погрешность чувствительности - возрастает пропорционально росту входной величины, а при установке на нуль = 0. Причинами могут быть: изменение коэффициента усиления усилителя, изменение жесткости пружины, изменение опорного напряжения в цифровом вольтметре.

Аддитивная мультипликативная

Выходные D_а D_м D_а+D_м

D_а D_м D_а+D_м

входные Х Х Х

Относительная погрешность - это отношение абсолютной погрешности измерения к истинному значению измеряемой величины.

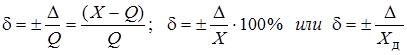
Недостатком относительной погрешности является то, что она при различных значениях Х принимает различные значения. Например: измеряем 2 длины: Q₁ = 5 мм., Х₁ = 5,1 мм; Q₂ = 6 мм., Х₂ = 6,1 тогда: D₁ = 5,1 – 5 = 0,1; D₂ = 6,1 – 6 = 0,1;

d₁ = 0,1 / 5 = 0,02; d₂ = 0,1 / 6 = 0,017.

Приведенная погрешность - это относительная погрешность, в которой абсолютная погрешность отнесена к условно принятому значению Q_N, которое является постоянным во всем диапазоне измерений, или его части. Условно принятое значение Q_N называют нормирующим. Чаще всего за него принимают верхний предел измерений данного средства измерения или Q_N - максимальное значение измеряемой величины.

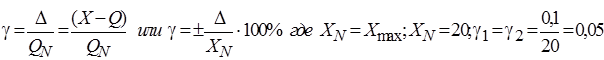
Погрешность прибора (инструментальные, аппаратные) - обусловлена погрешностью применяемого средства измерения (СИ). Эта погрешность может быть определена при испытаниях и занесена в паспорт прибора. Инструментальные погрешности являются следствием несовершенства или неправильности технологии изготовления СИ или их неисправностью, износом, старением.

Погрешность градуировки - погрешность действительного значения величины, приписанного той или иной отметке шкалы СИ в результате градуировки.

Основная погрешность - погрешность прибора, возникающая при нормальных условиях проверок и градуировок, оговоренных в технической документации.

Дополнительная погрешность - изменение показаний вследствие отклонения условий эксплуатации от нормальных.

Эксплуатационная погрешность - погрешность прибора в реальных условиях его эксплуатации. Складывается из основных и дополнительных погрешностей.

Методическая погрешность - это погрешность связанная не с самим прибором, а с методом проведения измерений. Эта погрешность может быть обусловлена:

- отличием принятой модели объекта измерения от модели, адекватно описывающей его свойство, которое определяется путем измерения;

- влиянием способов применения СИ;

- влиянием алгоритмов (формул), по которым производится вычисление результатов измерений, принятием тех или иных допущений, применением функциональных зависимостей;

- влиянием других факторов, не связанных со свойствами используемых СИ.

Примером методической погрешности может служить определение объема комнаты. Если умножить ширину, длину и высоту то получим не достаточно верный ответ, необходимо измерить все углы и высоту в них.

Статическая погрешность - погрешность СИ, применяемого при измерении ФВ, принимаемой за неизменную, т.е. свойственная условиям статического измерения.

Динамическая погрешность - погрешность СИ, возникающая при измерении изменяющейся в процессе измерений ФВ, т.е. свойственная условиям динамического измерения.

Правила округления результатов измерений:

1. Погрешность указывается двумя значащими цифрами, если первая из них = 1 или 2, и одной - если первая цифра = 3 и более. D = 0,17; D = 0,20; D = 0,3;

2. Результат измерения округляется до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасываются до того разряда, который соответствует разряду числового значения погрешности. D = 0,17 Х = 10 то следует записать Х = 10,00

3. Если цифра старшего отбрасываемого разряда < 5, то остальные цифры числа не меняются. Лишние цифры в целых числах заменяются 0, а в десятичных дробях отбрасываются. Х = 199709; D = 10 то следует записать Х = 199700.

4. Если цифра старшего из отбрасываемых разрядов ³ 5, но за ней следуют отличные от 0 цифры, то последнюю оставляемую цифру увеличиваем на 1. Х = 10,2365; D = 0,17 то следует записать Х = 10,24.

5. Если отбрасываемая цифра = 5, а следующие за ней цифры неизвестны или 0, то последнюю сохраняемую цифру числа не изменяют если она четная, и увеличивают на 1 если она не четная. Х = 10,235; D = 0,17 то следует записать Х = 10,24.

6. Округление производится в окончательном ответе, а все предварительные расчеты проводят с 2-3 лишними знаками.