Применение основных равносильностей алгебры высказываний

к решению задач»

Задание №1. Одна жительница древних Афин предостерегала сына: «Если ты будешь говорить правду, тебя возненавидят люди, а если ты будешь лгать, тебя возненавидят боги. Но ты должен или говорить правду, или лгать. Значит, тебя возненавидят люди или тебя возненавидят боги». Сын ответил матери: «Если я буду говорить правду, меня полюбят боги, а если буду лгать — меня полюбят люди. Но я должен или говорить правду, или лгать. Значит, меня полюбят или боги, или люди». Кто из них прав? (решить задачу двумя способами)

Указание:для доказательства удобно принять следующие обозначения: сын будет говорить правду — П, сын будет лгать - ; сына полюбят люди — Л, сына возненавидят люди - 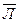; сына полюбят боги—Б, сына возненавидят боги - .

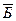(максимальное количество баллов – 10)

Задание №2 . Проверьте следующие равносильности двумя способами:

а) ;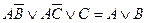

б) ;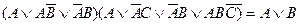

в) ;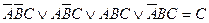

г) ;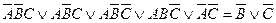

(максимальное количество баллов – 40)

Задание №3. Проверьте следующие равносильности, используя основные равносильности алгебры логики (предварительно упростив выражения, заключенные в скобки):

а) ;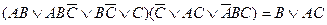

б) ;

в) ;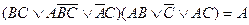

г) ;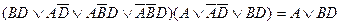

(максимальное количество баллов – 20)

Задание №4. Перевести на язык алгебры логики следующие высказывания:

1. Если светит солнце, то для того, чтобы не было дождя, достаточно, чтобы дул ветер;

2. Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя;

3. Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя;

4. Если ветра нет, то для дождя необходима пасмурная погода;

5. Если погода пасмурная и дует ветер, то дождя нет, но дождь идет, значит, нет ветра;

6. Неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра;

7. Если для солнечной погоды необходимо отсутствие дождя, то для того, чтобы пошел дождь, достаточно, чтобы погода была пасмурной и безветренной;

8. Будет ветреная погода, разве что пойдет дождь;

9. Дождь идет только тогда, когда погода пасмурная и безветренная, но дождя нет, значит, погода либо солнечная, либо пасмурная и ветреная;

10. Погода не только солнечная, но и безветренная, значит, дождя не будет, если не поднимется ветер;

11. Пойдет дождь, разве что поднимется ветер, значит, погода будет либо солнечной, либо пасмурной и ветреной;

12. Погода будет не только пасмурной, но и дождливой, несмотря на ветер. Значит, солнечной погоды не будет, разве что прекратится дождь.

(максимальное количество баллов – 60)

Указание:нужно каждый раз предварительно выделить элементарные высказывания и обозначить их заглавными буквами. Буквы удобнее всего выбирать так, чтобы всегда можно было бы быстро восстановить полный текст составного высказывания. Например: «светит солнце» можно обозначить буквой С, «дует ветер» — буквой В, «идет дождь» — буквой Д, «погода пасмурная» — буквой П.

Задание №5. Найдите отрицания следующих сложных высказываний:

1. Если пойдет дождь, Ваня, Петя и Коля останутся дома;

2. Коля решит задачу, если он вспомнит нужную теорему;

3. Хотя бы один из мальчиков (Ваня, Петя, Коля)-ошибается;

4. Ни один из мальчиков (Ваня, Петя, Коля) не опоздал в школу;

5. В кино пойдет либо Коля, либо Петя;

6. Если урок будет интересным, никто из мальчиков — Петя, Ваня, Коля — не будет смотреть в окно;

7. Будет солнечная погода, но хотя бы один из мальчиков — Петя и Ваня — не пойдет в лес;

8. Учитель рассказал смешную историю,но ник учеников — Петя и Ваня — не засмеялся;

9. Погода будет пасмурной, и Ваня пойдет в леси только тогда, когда в лес пойдет Коля;

10. Петя будет купаться только при солнечной погоде, если будет жарко.

(максимальное количество баллов – 50)

Указание:В высказываниях 7—9 ответ представить в виде импликации.