Понятие выводимости формулы из совокупности формул.Правила выводимости.

ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ.Определение формулы ИВ.система аксиом ИВ.

Исчисление высказываний – это аксиоматическая логическая система, интерпретацией которой является алгебра высказываний.

Описание всякого исчисления включает в себя описание символов этого исчисления (алфавита), формул, являющихся конечными конфигурациями символов, и определение выводимых формул.

Алфавит исчисления высказываний (ИВ) состоит из символов трёх категорий:

1.x, y, z, …, x₁, x₂, x₃, … - переменные высказывания.

2.¯, &, V, → - логические связки.

3.( ) – скобки.

Других символов ИВ не имеет.

Определение формулы ИВ

1.Всякое переменное высказывание – есть формула.

2.Если А – формула ИВ, то 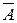- формула ИВ.

3.Если А и В формулы ИВ, то А & B, A V B, A → B – также формулы ИВ.

4.Никакая другая строка символов не является формулой ИВ.

Следующим этапом в построении ИВ является выделение класса доказуемых формул. Выделение класса доказуемых формул осуществляется путём применения аксиом ИВ и правил вывода.

Система аксиом исчисления высказываний

Система аксиом ИВ состоит из 11 аксиом, которые делятся на четыре группы.

I₁: x → ( y → x ) ;

I₂: ( x → ( y → z ) ) → ( ( x → y ) → ( x → z ) ) ;

II₁: x & y → x ;

II₂: x & y → y ;

II₃: ( z → x ) → ( ( z → y ) → ( z → x & y ) ) ;

III₁: x → x V y ;

III₂: y → x & y ;

III₃: ( x → z ) → ( ( y → z ) → ( x V y → z ) ) ;

IV₁: ( x → y ) → ( → ) ;

IV₂: x → ;

IV₃: → x .

Аксиомы ИВ определяют исходный класс доказуемых формул. Доказуемая формула А обозначается |­—А.

Определение доказуемой формулы исчисления высказываний.Правило подстановки.Правило заключения.

Доказуемая формула А обозначается |­—А.

Правила вывода.

1. Правило подстановки. Пусть А – доказуемая формула ИВ, x – переменная, В – любая формула ИВ. Тогда формула, которая получается из формулы А путём подстановки в неё вместо x формулы В, доказуема. Операция подстановки обозначается:

.

Тогда правило подстановки записывается так:

.

2. Правило заключения. Если формулы B, B → C – доказуемые формулы ИВ, то формула С – доказуема.

.

Вообще доказуемой формулой называется всякая формула, которая или является аксиомой, или получается из доказуемых формул с помощью правил подстановки и заключения.

3. Производные правила вывода:

I. - правило одновременной подстановки.

II. - правило силлогизма.

III. - правило контрапозиции.

IV.а) , б) - правила снятия двойного отрицания.

V. - правило сложного заключения.

Понятие выводимости формулы из совокупности формул.Правила выводимости.

Пусть имеется конечная совокупность формул ИВ Н = {A₁, A₂, …, A_n}. Говорят, что формула B выводима из совокупности H ( H |­— B ), если:

а) либо B Є H,

б) либо B – доказуемая формула ИВ,

в) либо B получается по правилу заключения из формул C и C → B, которые выводимы из совокупности H.

Также говорят, что конечная совокупность формул B₁, B₂, …, B_k есть вывод из H, если для каждой формулы B_i ( i = 1, 2, …, k ) этой совокупности:

а) либо B_i Є H,

б) либо B_i доказуема,

в) либо B_i получается по правилу заключения из формул C, C → B_i, которые находятся в выводе, предшествуя B_i.

Правила выводимости

Пусть H и W – две совокупности формул исчисления высказываний. Будем обозначать через H,W их объединение, то есть

H,W = H W.

В частности, если совокупность W состоит из одной формулы C, то будем записывать объединение H {C} в виде H,C.

Тогда имеют место правила выводимости:

1. .

2. .

3. .

4. .

5. - теорема дедукции.

6. - обобщённая теорема дедукции.

7. - правило введения конъюнкции.

8. - правило введения дизъюнкции.

9. - правило перестановки посылок.

10. - правило соединения посылок.

- правило разъединения