Лабораторная работа №2. Мощность в цепи переменного тока

Оглавление

Предисловие..............................................................................................................................................2

Лабораторная работа №1. Изучение последовательного и связанных колебательных контуров....3

Лабораторная работа №2. Мощность в цепи переменного тока и методы её измерения................11

Лабораторная работа №3. Изучение полевых транзисторов..............................................................17

Лабораторная работа №4. Снятие характеристик полупроводниковых триодов и определение

их параметров..........................................................................................................................................25

Лабораторная работа №5. Усилители напряжения низкой частоты..................................................33

Лабораторная работа №6. Изучение выпрямительных схем..............................................................39

Лабораторная работа №7. Изучение однофазного трансформатора..................................................49

Лабораторная работа №8. Изучение мультивибраторов и триггеров................................................55

Лабораторная работа №9. Исследование работы транзисторного ключа.........................................65

Лабораторная работа №10. Изучение электронных схем элементов или, и, не, или-не, и-не, и

дешифратора с трёхразрядным счётчиком..........................................................................................75

Лабораторная работа №11. Исследование регистра сдвига на базе R,S - триггеров........................83

Лабораторная работа №12. Цифро-аналоговый преобразователь......................................................89

Лабораторная работа №13. Знакогенераторы ЭВМ.............................................................................97

Предисловие

Курс «Промышленная электроника» предназначена для подготовки студентов по специальности «Электроэнергетика» в области электроэнергии и электротехники.

Технический прогресс современной техники широко базируется на применении электронных устройств. Курс относится к общеинженерным дисциплинам и не ставит своей задачей подготовку специалистов в области электронной схемотехники.

Целью курса «Промышленная электроника» является изучение принципа действия и возможности электронных устройств, формирование навыков расчетов, измерение параметров и характеристик аналоговых и цифровых электронных устройств.

Задачи курса – сформировать необходимый минимум специальных теоретических и практических знаний, которые обеспечили бы возможность понимать и анализировать процессы в электронных цепях.

При изложении курса большое внимание уделяется электронным приборам, импульсных и цифровым устройствам. В рамках теории электронных цепей изучаются такие квазилинейные устройства, как усилители. Рассматриваются выпрямители однофазного и трехфазного тока, стабилизаторы напряжения.

В результате освоения курса «Промышленная электроника» студент должен:

• иметь представление об электронике как основной технической базе при создании современных информационных систем;
• знать основы элементной базы современных аналоговых и цифровых устройств;
• знать основы анализа базовых элементов и устройств радиоэлектронной аппаратуры;
• знать принцип работы элементов электронных приборов и физические процессы, протекающие в них.

Курс «Промышленная электроника» читается на 3 курсе, рассчитан на 40 часов, из них 20 часов – лекций, 20 часов – практических занятий. Контроль за эффективностью усвоения курса проводится систематически на практических занятиях, в конце шестого семестра – зачет.

В программе дан подробный перечень вопросов, рассматриваемых в лекционном курсе и на практических занятиях, приведен список основной и дополнительной литературы.

Дисциплина входит в состав федерального компонента цикла специальных дисциплин государственного общеобразовательного стандарта высшего профессионального образования второго поколения для специальности – Профессиональное обучение, специализации 050501.19 электроэнергетика, электротехника и электротехнологии.

Лабораторная работа №1. Изучение последовательных и связанного колебательных контуров

Цель работы: Построить амплитудно-частотные характеристики последовательного и связанных колебательных контуров, определить параметры контуров, изучить явление резонанса напряжений.

Приборы и оборудование:

1.Генератор стандартных сигналов Г4-18А.

2.Катодный вольтметр ВКС - 7в.

3.Миллиамперметр.

4.Набор катушек и конденсаторов.

5.Монтажные провода.

Теоретические замечания.

Колебательный контур представляет собой один из основных элементов радиосхем. Схема замещения контура с сосредоточенными параметрами с учетом потерь энергии, представлена на рис.1.

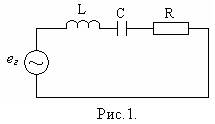
Активное сопротивление R введено для учета потерь энергии в контуре. В реальном колебательном контуре L,С,R распределены по всей схеме. На схеме, представленной на рис.1 параметры L,С,R "привязаны" к определенному участку схемы. Такая идеализация допустима, если размеры элементов контура много меньше длины волны колебаний.

Резонансная частота ω_pколебательного контура определяется из условия равенства нулю реактивной составляющей полного сопротивления колебательного контура

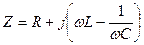
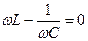или

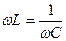
Отсюда: 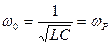, где 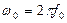собственная частота контура.

Характеристическим сопротивлением ρ называется сопротивление индуктивности или емкости на резонансной частоте:

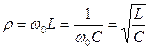
Пусть контур (рис.1) подключен к источнику внешней ЭДС

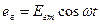
По закону Кирхгофа: .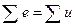

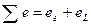, где 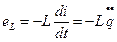– ЭДС самоиндукции,

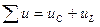, где

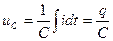- напряжение на конденсаторе,

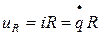– напряжение на активном сопротивлении.

В соответствии с законом Кирхгофа получаем:

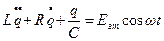(1)

Если е_г=0, в контуре совершаются свободные затухающие колеба­ния, уравнение (1), описывающее свободные колебания, примет вид:

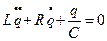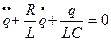, или (1а)

Обозначив через 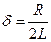(коэффициент затухания), 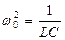(ω₀ –собственная частота контура), получим уравнение (1а) в виде:

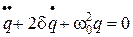(2).

Если 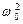>> 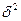(этот случай наиболее инте­ресен для радиотехники), решение (2) может быть записано в ви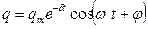де:

, где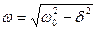

Зависимость заряда на конденсаторе от времени (рис.2) имеет ха­рактер затухающих колебаний, частота которых ωназывается частотой свободных колебаний.

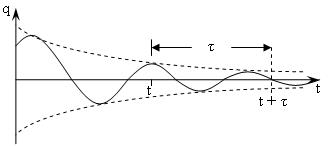
Рис.2.

Для характеристики скорости процесса затухания свободных колебаний в контуре пользуются коэффициентом затухания δ, логарифми­ческим декрементом затухания dи добротностью контура Q.

1.Коэффициент затухания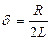

Возьмем промежуток времени τ=NT до истечении которого амплитуда колебаний уменьшается в " e " раз.

,

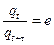
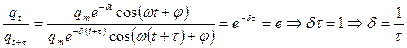Таким образом коэффициент затухания δ – величина обратная времени, по истечении которого амплитуда колебаний уменьшается в "e"раз.

2.Логарифмический декремент затухания dхарактеризует уменьшение амплитуд колебаний, за период, он равен натуральному логарифму отношения .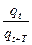

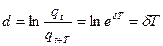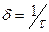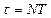Учитывая, что , , а получим:

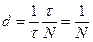
Следовательно, логарифмический декремент затухания – это величина обратная тому числу полных колебаний, по истечении которых амплиту­да колебаний уменьшается в “e” раз.

3.Добротность Q характеризует относительную убыль энергии в процес­се колебаний:

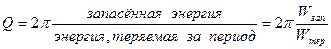
Энергия, теряемая в контуре, идет на потери в активном сопротивлении:

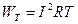
Энергия, запасенная колебательной системой, равна максимальной энергии, накопленной конденсатором или индуктивностью:

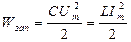
тогда:

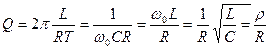
Величина, обратная добротности, называется затуханием контура:

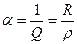
Если к контуру подвести внешнюю ЭДС, то решение уравнения (1) равно сумме общего решения однородного уравнения (описывающие свободные колебания в контуре) и частного решения неоднородного (описывающего вынужденные колебания в контуре). Так как свободные колебания имеют затухающий характер, то ими можно пренебречь и считать, что в конту­ре существуют лишь вынужденные колебания:

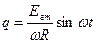(3)

Рассмотрим случай резонанса, когда 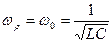,при этом уравнение (3), примет вид:

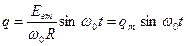
Амплитуда напряжения на конденсаторе равна:

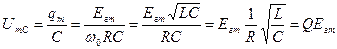
или:

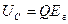
Амплитудно-частотная характеристика последовательного колеба­тельного контура приведена на рис.3. Разность между частотой источника напряжения и резонансной частотой принято называть абсолютной растройкой контура:

,

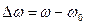аотношение 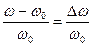- относительной растройкой.

Среди ЭДС одинаковых амплитуд, но не одинаковых частот, наибольший ток создает та, для которой величина растройки наименьшая. Иными словами, из всех ЭДС, воздействующих на контур, последний “избирает” некото­рый, вполне определенный спектр частот. Это свойство контура называ­ется частотной избирательностью.

Избирательные свойства колебательного контура определяются шириной его резонансной характеристики.

Диапазон частот, пропускаемых контуром, характеризуют полосой пропускания контура - областью частот, в пределах которой амплитуда колебаний тока (или напряжения) уменьшается менее чем в 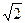раз по сравнению с резонансом. Это соответствует уменьшению мощности при резо­нансе в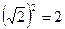раза, т.е.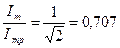

Полоса пропускания контура определяется равенством:

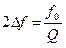
Влияние добротности контура на полосу пропускания отражено на ампли­тудно-частотной характеристике (рис. З).

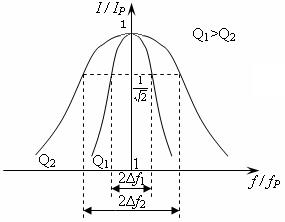
Рис.3.

При добротности Q₂характеристика менее острая, чем при более высокой добротности Q₁и поэтому полоса пропускания контура 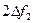с добротностью Q₂ шире, чем полоса пропускания контура 2Δf₁ с добротностью Q₁. Для воспроизве­дении радиосигнала полоса пропускания контура должна быть не менее ширины ос­новной части спектра радиосигнала. Если же это требование не выполняется, при­ходится снижать добротность контура, но тогда ухудшается его избирательность.

Противоречие между избирательностью и полосой пропускания не может быть решено полностью, если в схеме используется одиночный колебатель­ный контур.

В радиоаппаратуре колебательный контур обычно связан с другими цепями, в которые передается часть энергии, поступающей от внешнего источника. Контур, колебания в котором возбуждаются внешним источни­ком, называется первичным, а тот, в который передается часть энергии называется вторичным.

Энергия, подводимая от внешнего источника к первичному контуру, расходуется не только в нем, но и частично передается во второй кон­тур. Потребление вторичным контуром энергии из первичного эквивалент­но включению в первичный контур активного сопротивления, потребляю­щего тоже самое количество энергии, которое потребляет вторичный контур. Поэтому говорят, что в результате связи вторичный контур вносит в первичный некоторое сопротивлени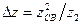е , где 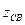- сопротивление связи. Это приводит к уменьшению добротности и резо­нансного сопротивления контура.

Контуры могут быть связаны между собой различными способами. Например, если катушки контуров расположить близко одну к другой, то часть переменного магнитного потока, создаваемого током в обмотке первичной катушки, будет пронизывать витки катушки вторичного контур и наводить в нем переменную ЭДС E₁₂ величину которой можно опре­делить по закону электромагнитной индукции:

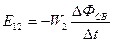
где 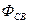- поток связи, W₂ - число витков катушки вторичного контура_. Если ток меняется по синусоидальному закону, то 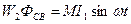где М - коэффициент пропорциональности, называемый коэффициентом взаимоиндукции.

Вводят понятие коэффициента связи χ₁₂, определяемого как отношение 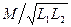. Если числитель и знаменатель этого отношения умножить на I₁ω, то окажется, что коэффициент связи выражает отношение ЭДС, наведен­ной во вторичном контуре, к напряжению на индуктивности первичного контура: 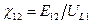. Причём, .

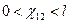Амплитуда наведенной ЭДС в катушке вторичного контура:

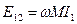
Величина ωM имеет размерность сопротивления и называется сопротив­лением связи .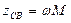

С увеличением коэффициента взаимной индукции М ЭДС, наводимая во вторичном контуре, возрастает.

В связанных контурах, имеющих одну и ту же частоту собственных колебаний, при некоторых условиях может возникнуть резонанс не толь­ко на частоте собственных колебаний, но и еще на двух других час­тотах, которые можно определить по формуле:

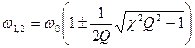
Частоты ω_1,2 называют частотами связи, или нормальными частотами системы.

При некоторой частоте, меньшей частоты собственных колебаний, сопротивление контуров имеет емкостный характер. Наведенная во вторичном контуре ЭДС E₁₂ отстает на 90^° относительно тока в пер­вичном контуре I₁(рис.4).

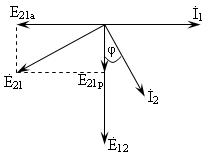
Рис.4.

Так как сопротивление вторичного контура имеет емкостный характер, то ток в нем I₂ опережает ЭДС Е₁₂ на угол φ. ЭДС E₂₁,наводи­мая в первичном контуре вторичным отстает от тока I₂ на угол 90^°. Эту ЭДС можно разложить на две составляющие: первая E_21a имеет направление, противоположное вектору тока в первичном контуре, вторая E_21pотстает от него на 90^°. Таким образом, первая составля­ющая E_21a стремится уменьшить ток в первичном контуре, что равносильно увеличению активного сопротивления первичного контура, а вторая E_21p увеличивает ЭДС катушки, которая отстает от тока на 90^°, что равносильно увеличению ее индуктивности. Говорят, что при емкостном сопротивлении вторичного контура в первичный контур вносится активное сопротивление и индуктивное. При доста­точно большой связи, при некоторой растройке контуров относительно частоты источника вносимое индуктивное сопротивление скомпенсирует собственное емкостное сопротивление контура. При этом контур представляет собой для источника переменной ЭДС чисто активное сопротивление, и в системе контуров имеет место резо­нанс. Благодаря этому токи в первичном и во вторичном контурах резко возрастают. Нетрудно убедиться, что аналогичная картина может наблю­даться и на частоте, превосходящей частоту собственных колебаний контура, т.е. оказывается, что система из двух одинаковых достаточно сильно связанных контуров обладает тремя резонансными частотами, одна из которых является частотой их собственных колебаний ω₀, другая несколько ниже ω₁<ω₀, а третья выше ω₂> ω₀. Две последние резо­нансные частоты называются частотами связи.

Разность между частотами ω₁ и ω₂тем больше, чем больше коэффи­циент связи; при связи меньше некоторого значения, называемой крити­ческой, вносимых реактивных сопротивлений не хватает для компенсации собственных реактивных сопротивлений контура и резонанс имеет место только на частоте собственных колебаний контуров. По этому при связи меньше критической резонансная характеристика (рис.5 кривая №1) напоминает характеристику одиночного контура. При связи больше крити­ческой резонансная характеристика приобретает вид двугорбой кривой, максимумы которой соответствуют частотам связи ω₁ и ω₂ (кривая №2):

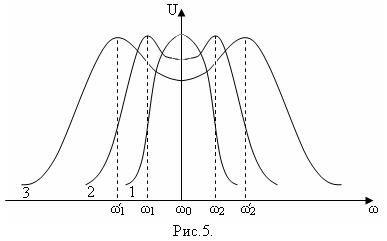
При более сильной связи частоты ω₁и ω₂ расположены еще дальше друг от друга (кривая №3).

Задание 1.

Ознакомтесь с оборудованием, используемым при снятии амплитудно-частотной характеристики одиночного колебательного контура. Соберите схему по рис.6 сначала без дополнительного сопротивления и снимите резонансную характеристику контура.

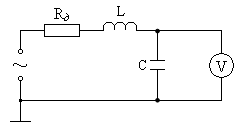
рис.6

Для этого установите на выходе Г4-18А напряжение 1В и все время поддерживайте его постоянным. Переключатель диапазона частот поставьте в по­ложение 2. Для построения резонансной характеристики контура необхо­димо произвести 8-10 измерений до резонанса и столько же после. Вблизи резонанса частоту генератора надо изменять через малые интер­валы. Снимите резонансную кривую контура.

Добротность можно рассчитать по формуле:

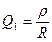(4)

Полученные данные занести в таблицу 1:

Таблица 1.

fКГц

UC

UC / UРез

f / fРез

Rд

Zк

Затем снимите резонансную кривую контура с дополнительным сопро­тивлением R_д. Измерения производить на тех же частотах, что и в предыдущем случае. Добротность контура в этом случае равна:

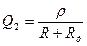(5)

Полученные данные занести в таблицу 1. Из формул 4 и 5 получаем:

Добротность контура при резонансе определяется по формуле:

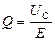
По результатам измерения построить три резонансные кривые в одной системе координат:

,

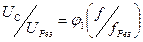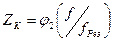
Рассчитать основные параметры контура при резонансе и результаты занести в таблицу 2.

Таблица 2.

Q

R

d

δ

2∆f

L

C

Rд

Рассчитайте период колебаний по формуле: 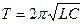. Зная период колебаний, найдите резонансную частоту. Полученные результаты сравнить с экспериментальными.

Задание 2.

Собрать схему (рис.6) с другим конденсатором. Снять резонансную кри­вую контура. Выяснить, как влияет величина емкости на параметры кон­тура. Полученные результаты занести в таблицу 2. Построить резонансную кривую.

Задание 3.

Снять резонансные характеристики связанных контуров. Установить минимальную связь между контурами, собрав схему по рис.7.

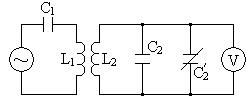
рис.7

Найти резонансную частоту первичного контура. Изменяя емкость вторич­ного контура подстроечным конденсатором, настроить вторичный контур в резонанс с первичным. Снять четыре резонансные кривые контура:

1.Связь критическая (напряжение во втором контуре на резонансной частоте максимальное).

2.Связь меньше критической.

3.Связь немного больше критической.

4.Максимальная связь.

Для построения каждой резонансной кривой произвести по 6-20 измерений. Данные измерений занести в таблицу 3.

Таблица 3.

U

f

f / fРез

U / UРез

По полученным данным построить четыре графика в одной системе координат:

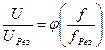
КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Какие особенности работы и основные соотношения для:

а.) Идеального колебательного контура?

б.) Последовательного контура с сосредоточенными параметрами?

в.) Параллельного контура?

г.) Связанных контуров?

2. Какие существуют параметры контура? Их физический смысл. В каких единицах они измеряются?

3. Что называется полосой пропускания контура?

4. Как графически определить полосу пропускания контура?

5. От чего зависит острота резонансной кривой контура?

6. Какая связь называется критической? слабой? больше критической?

7. Физический смысл коэффициента связи.

8. Чему равны частоты связи?

9. Чему равна полоса пропускания связанных контуров при слабой связи? критической связи? оптимальная полоса пропускания?

10. Фильтрующие свойства последовательного контура.

11. Фильтрующие свойства параллельного колебательного контура.

Лабораторная работа №2. Мощность в цепи переменного тока

и методы её измерения.

Цель работы:Изучение методов измерения активной, реактивной и полной мощностей в цепи переменного тока. Ознакомление с принципом действия и применением электроди­намических ваттметра и фазометра.

Теоретические замечания.

Потребляемая в цепи мощность равна произведению напряжения на зажимах этой цепи на силу тока. При переменном токе это справедливо только для мгновенной мощности p:

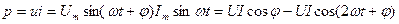(1)

Периодически изменяющаяся мощность p мало удобна для оценки энергетического состояния цепи переменного тока. Поэтому основной энергетической характеристикой цепи переменного тока является средняя (активная) мощность, которая равна:

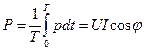(2)

Мощность P принято измерять в ваттах (Вт).

Множитель cosφ в выражении (2) называется коэффициентом мощности, так как при неизменных напряжении и токе в цепи актив­ная мощность в зависимости от cosφ меняется от нуля до макси­мального значения. Наибольшее значение активной мощности называется полной (или кажущейся) мощностью, которая в отличие от активной мощности измеряется в вольт-амперах (ВА).

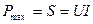(3)

Мерой реактивной энергии является реактивная мощность.

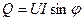(4)

Единицей реактивной мощности является ВАр (Вольт-Ампер реактивный).

Из (2),(3) и (4) следует, что

P=Scosφ ; Q=Ssinφ ; P²+Q²=S².

Полная мощность легко рассчитывается по показаниям вольтмет­ра и амперметра, а активная и реактивная мощности могут быть измере­ны непосредственно с помощью специальных приборов. Можно фазомет­ром измерить величину фазового сдвига φ, а затем вычислить Р и Q.

Рассмотрим подробно работу электродинамического ваттметра, предназначенного для непосредственного измерения активной мощности (принцип действия ферродинамического ваттметра аналогичен).

Измерительный механизм ваттметра электродинамической систе­мы состоит из неподвижной катушки, содержащей малое число витков толстого провода (токовая катушка), и подвижной катушки, имеющей большое число витков тонкого провода (катушка напряжения). Из теории работы электродинамических приборов известно, что мгновенный вращающий момент, действующий на подвижную систему, прямо пропорцио­нален произведению токов в катушках: m=k i₁i₂

Через первую катушку, включенную последовательно с нагрузкой, про­ходит ток цепи:

i₁=i=I_msinωt

Катушка напряжения через безреактивное добавочное сопротивление включается параллельно нагрузке, поэтому

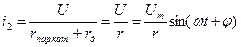
Среднее за период значение вращающего момента равно

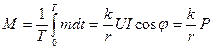
Равновесие подвижной части наступает при M_ср=M_тор=Dα (D – коэффициент, определяемый упругостью пружин). Следовательно, угол поворота подвижной системы

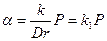
прямо пропорционален активной мощности.

Коэффициент пропорциональности k₁ зависит от величины добавочного сопротивления r_д, которое различно при разных пределах измерения ваттметра по напряжению. Кроме того, этот коэф­фициент окажется другим, если ток i₁ будет в несколько раз отличаться от тока iцепи (например, при использовании трансформатора тока для расширения пределов измерения ваттметра по току). Величина коэффициента пропорциональности учитывается при определении цены деления ваттметра.

Мощность, приходящаяся на одно деление шкалы ваттметра, называется ценой деления при заданных пределах измерения по напряже­нию U_Ни току I_Н. Цена деления C_w опреде­ляется по формуле: 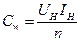, здесь n – число делений на шкале ваттметра.

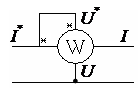
рис 1.

Ваттметр включается по четырехзажимной схеме рис.1. Два токовых за­жима обозначаются I^* и I. При помощи этих зажимов то­ковая катушка ваттметра включается в схему последовательно с нагрузкой (положительным считается направление тока от I^* к I).Параллельно нагрузке ваттметр подключается при помощи второй пары зажимов U^* и U (положительным считается направление тока в параллельной цепи ваттметра от U^* к U).

Зажим U^* можно подключать как к клемме I^* , так и к клемме I , стрелка ваттметра все равно будет отклоняться вправо. В первом случае ваттметр измеряет суммарную мощность, потребляе­мую нагрузкой и токовой катушкой ваттметра P +P_I , во втором – нагрузкой и параллельной ветвью ваттметра P +P_U. Так как P_I < P_U , ошибка при измерении мощности, потребляемой нагруз­кой, будет меньше в первом случае, когда соединены клеммы помечен­ные звездочками U^* и I^* (так называемые генераторные за­жимы ваттметра).

В цепи трехфазного переменного тока при симметричной системе напряжений электродинамическим ваттметром можно непосредственно измерить не только активную, но и реактивную мощности. В самом деле, линейное напряжение U_ВС отстает от фазного U_Aна угол 90°. Если через токовую обмотку ваттметра пропустить фазный ток I_А, параллельную цепь его подключить к линейному напря­жению U_ВС (U^* – в, U – с), то показания прибора будут определяться соотношением:

,

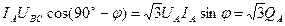то есть ваттметр будет показывать мощность в 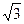раз большую реактивной мощности фазы А.

Электродинамический фазометр представляет собой логометр той же системы, то есть имеет две подвижных катушки. Неподвижная (то­ковая) катушка включается последовательно в цепь с приемником энергии. Последовательно с одной из подвижных катушек включается безреактивное добавочное сопротивление r_д , последовательно с другой – реактивная катушка с сопротивлением x_Lд. Подвижные катушки вместе с добавочными сопротивлениями образуют две параллельные ветви, которые включены также параллельно сопро­тивлению нагрузки. В первой из подвижных катушек ток I₁ совпадает по фазе с напряжением U,а в другой – ток I₂ отстает от напряжения на 90°. Известно, что угол поворота подвиж­ной системы электродинамического логометра определяется соотношением:

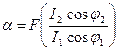
В нашем случае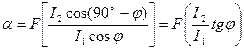

Параллельные цепи прибора обладают постоянным сопротивлением при неизменной частоте тока, следовательно,

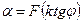
то есть угол поворота подвижной системы фазометра зависит от вели­чины сдвига фаз между напряжением на нагрузке и током в ней. Поэто­му на шкале фазометра могут быть нанесены значения угла φ(или cosφ).

Фазометр включается в цепь по 4-х зажимной схеме аналогично ваттметру.

Задание для самостоятельной работы.

1. Схему включения ваттметра в цепь (рис.1) перечертите в тетрадь. Укажите на схеме в тетради зажимы I^* , I, U^*и U. Как определить цену деления ваттметра?

2. Начертите схему включения ваттметра при измерении мощности в це­пи постоянного тока. Укажите полярность подключения источника тока, последовательной и параллельной цепей ваттметра, приемника тока.

3. Как изменятся показания ваттметра, если изменить полярность включения одной из его катушек?

4. Определите показания всех приборов в схеме (рис.2).

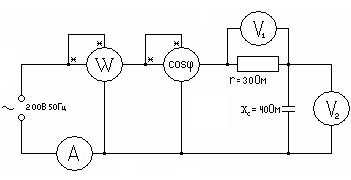
рис.2

Чему равны полная и реактивная мощности цепи? Постройте вектор­ную диаграмму для иллюстрации работы этой цепи. Укажите знак уг­ла сдвига фаз между напряжением и током.

5. В цепи переменного тока напряжение и ток изменяются по законам:

,

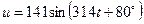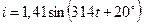
Рассчитайте полную, активную и реактивную мощности цепи.

6. Напряжение на катушке 200В, частота тока 50Гц. Активная мощность, потреб­ляемая катушкой 640 Вт, а ток в ней 4А. Определите активное сопротивление катушки и ее индуктивность.