Степени вершин и подсчет числа ребер графа
Введем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.
Задача 3. В городе М 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным 15×5/2=37,5. Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.
Ответ. Соединить телефоны таким образом невозможно.
Теорема: Любой граф содержит четное число нечетных вершин.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Связность графа
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называется связным, если из любые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.
Задача 4. В стране С 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города можно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:
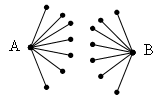
Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.
Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: “Доказать, что граф дорог страны С связен.”
Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:
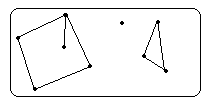
Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:
Задача 5. В государстве Н только один вид транспорта – поезд. Из столицы выходит 21 железнодорожная колея, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно доехать в город Дальний.
Доказательство: Понятно, что если нарисовать граф ж/д путей государства Н, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу государства. Из столицы выходит 21 ж/д колея, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ж/д путям до города Дальний, что и требовалось доказать.
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
Задача 6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?
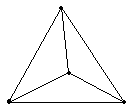
Решение. Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.
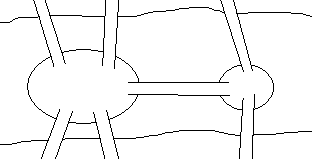
И в заключение – задача о Кенигсбергских мостах.
Задача 7. На рисунке изображена схема мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?
Алгоритм Дейкстры отыскания кратчайшего пути на графе.
К таким задачам сводятся различные оптимизационные задачи. Если , например, граф изображает сеть дорог или коммуникаций, соединяющих некоторые пункты, длина дуги соответствует расстоянию, стоимости или времени поездки, то задача заключается в выборе минимального пути с точки зрения либо его длины, либо стоимости поездки, либо затрат времени.
Вершины графа могут представлять собой этапы решения задач при различных вариантах, а соединяющие их дуги направления решения. Если при этом рассматривать длительность каждого этапа решения, то будем иметь нагруженный ориентированный граф.
Одним из способов решения данной задачи является алгоритм Э. Дейкстры, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году, который покажем на примере.
Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.
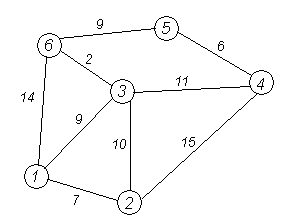
Кружками обозначены вершины, линиями — пути между ними (рёбра графа). В кружках обозначены номера вершин, над рёбрами обозначена их «цена» — длина пути. В процессе поиска минимального пути всем вершинам графа приписываются метки (числа), которые подразделяются на постоянные (они подчеркиваются) и временные. Метку вершины 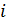 будем обозначать
будем обозначать 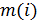 . Процесс вычисления меток для наглядности представим в виде таблицы.
. Процесс вычисления меток для наглядности представим в виде таблицы.
| Шаг\вершины | ||||||
| Первый шаг | 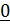 | 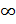 | 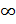 | 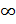 | 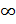 | 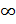 |
| Второй шаг |  | 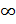 | 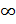 | |||
| Третий шаг | 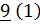 | 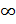 | ||||
| Четвертый шаг | 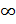 | 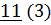 | ||||
| Пятый шаг | 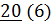 |
В столбцах таблицы указываются метки вершин, которые они имеют в процессе работы алгоритма. Так в первом столбце указаны метки вершины 1, во втором метки второй вершины и т.д. Таким образом за каждой вершиной закреплен свой столбец.
Для восстановления кратчайшего пути рядом с каждой подчеркнутой меткой в скобках указывается вершина предыдущего шага с постоянной меткой. Если таких вершин несколько, выбирается любая из них, поскольку нужно найти один кратчайший путь. При указании всех таких вершин перебором получаются все кратчайшие пути.
В процессе работы начальные вершины меняются, для их обозначения будем использовать общий символ (н).
На первом шаге вершине 1 приписывается начальная постоянная метка 0 (она подчеркнута), а всем остальным вершинам временные метки 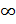 . На каждом следующем шаге вершине
. На каждом следующем шаге вершине 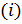 , соединенной дугой с начальной вершиной (н), приписывается метка, равная минимальному из чисел
, соединенной дугой с начальной вершиной (н), приписывается метка, равная минимальному из чисел 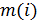 и
и 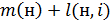 , где
, где 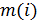 -прежняя метка
-прежняя метка 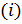 -ой вершины, а
-ой вершины, а 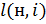 -длина дуги, соединяющей вершину (н) с вершиной
-длина дуги, соединяющей вершину (н) с вершиной 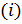 .
.
Рассмотрим второй шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме значения метки вершины 1 и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7. Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й. Полученные соответственно значения 9 и 14 заносим в столбцы 3 и 6 таблицы. Из полученных значений выбираем минимальное 7 его подчеркиваем и берем вершину 2 за начальную.
Третий шаг. Пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Следующий сосед вершины 2 — вершина 3, так как имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а это меньше 17, поэтому метка не меняется. Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна сумме кратчайшего расстояния до 2-й вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 = 22). Поскольку 22< 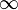 , устанавливаем метку вершины 4 равной 22.
, устанавливаем метку вершины 4 равной 22.
Четвертый шаг. Повторяем алгоритм, выбрав за начальную вершину 3. После ее обработки результаты занесем в таблицу и вершину 6 возьмем за начальную.
Пятым шагом алгоритм закончится на 5-ой вершине с меткой 20.
Результат работы алгоритма находим по таблице: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11. Восстанавливаются эти кратчайшие пути по вершинам в скобках в таблице. Например восстановим путь из вершины 1 в вершину 5. Двигаемся из конечной вершины 5, в которую в минимальном пути ведет дуга из вершины 6. В вершину 6 попадаем из вершины 3, в 3 приходим из начальной вершины 1.Следовательно, искомый кратчайший путь: 1- 3- 6- 5.
Задания
1. На квадратной доске 3x3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?
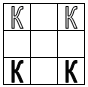 Рис. 1 Рис. 1 | 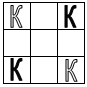 Рис. 2 Рис. 2 |
2. В стране Ц есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?
3. В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
4. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей ?
5. У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей ?
6. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
7. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.
8. В стране из каждого города выходит 100 дорог и из каждого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.
9. Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту розно 1 раз. На острове Т он побывал трижды. Сколько мостов ведет с Т, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
10. На рисунке изображен парк, разделенный на несколько частей заборами. Можно ли прогуляться по парку и его окрестностям так, чтобы перелезть через каждый забор ровно 1 раз?
| Начало формы Конец формы | |
| 11. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет). Определите длину кратчайшего маршрута из А в F. | |
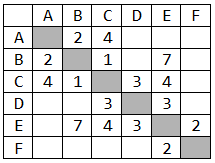 | |
| 12. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет). Определите длину кратчайшего маршрута из А в B. | |
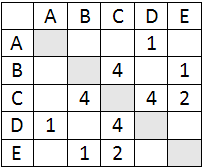
Функции
