Сети Петри для моделирования

Сети Петри

Основные определения

Сети Петри (СП) и их многочисленные модификации являются одним из классов моделей, неоспоримым достоинством которых является возможность адекватного представления не только структуры сложных организационно-технологических систем и комплексов, но также и логико-временных особенностей процессов их функционирования. Сети Петри представляют собой математическую модель для представления структуры и анализа динамики функционирования систем в терминах «условие-событие». Это модель может быть успешно использована для описания так называемых динамических дискретных систем различных классов, таких как: вычислительные процессы и программы, технологические процессы, информационные, экономические, биологические, социальные и технические системы.

Модели сетей Петри позволяют исследовать работоспособность моделируемых систем, оптимальность их структуры, эффективность процесса их функционирования, а также возможность достижения в процессе функционирования определенных состояний. Сети Петри и их обобщения являются удобным и мощным средством моделирования асинхронных, параллельных, распределенных и недетерминированных процессов, позволяют наглядно представить динамику функционирования систем и составляющих их элементов. Свойство иерархического вложения сетей Петри позволяют рассматривать модели различной степени детализации, обеспечивая тем самым необходимую композицию сложных систем и процессов.

Структура сети Петри.Сеть Петри С является четверкой: С = (Р, Т, I, О). Р— {p₁, р₂, ..., р_n} — конечное множество позиций, n³ 0. Т = (t ₁, t ₂, ..., t _m} — конечное множество переходов, m ³ 0. Множество позиций и множество переходов не пересекаются, Р ∩ Т = Ø. I : T → Р^∞ является входной функцией — отображением из переходов в комплекты позиций.
О: Т → Р^∞есть выходная функция — отображение из переходов в комплекты позиций.

Позиция р_i является входной позицией перехода t_jв том случае, если p_iÎ I(t_j); p_iявляется выходной позицией, если р_iÎ O(t_j). Входы и выходы переходов представляют собой комплекты позиций. Комплект является обобщением множества, в которое включены многократно повторяющиеся элементы — тиражированные элементы. Использование комплектов, а не множеств для входов и выходов перехода позволяет позиции быть кратным входом либо кратным выходом перехода. Кратность входной позиции p_iдля перехода t_jесть число появлений позиции во входном комплекте перехода, #(p_i, I(t_j)). Аналогично кратность выходной позиции p_iдля перехода t_jесть число появлений позиции в выходном комплекте перехода, #(p_i, О(tj)). Если входная и выходная функции являются множествами (а не комплектами), то кратность каждой позиции есть либо 0, либо 1.

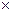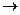Существует и такой вариант определения входной и выходной функций переходов. I – входная функция переходов, которая определяется как отображение I: P T N₀; O – выходная функция переходов, которое определяется как отображение O: T 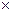P 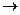N₀, где N₀ – множество натуральных чисел и ноль.

Пример. C = (P, T, I, O), P = {p₁, p₂, p₃, p₄, p₅}, T = {t₁, t₂, t₃, t₄},

I ( t₁) = {p₁}, O(t₁) = {p₂, p₃, p₅},

I ( t₂) = {p₂, p₃, p₅}, O(t₂) = {p₅},

I( t₃) = {p₃}, O(t ₃) = {p₄},

I( t₄) = {p₄}, O(t ₄) = {p₂, p₃},

Графическое представление сети Петри. Структура сети Петри представляет собой совокупность позиций и переходов. В соответствии с этим граф сети Петри обладает двумя типами узлов. Кружок  является позицией, а планка | - переходом.

Ориентированные дуги (стрелки) соединяют позиции и переходы, при этом некоторые дуги направлены от позиций к переходам, а другие — от переходов к позициям. Дуга, направленная от позиции p_iк переходу t_j, определяет позицию, которая является входом перехода. Кратные входы в переход указываются кратными дугами из входных позиций в переход. Выходная позиция указывается дугой от перехода к позиции. Кратные выходы также представлены кратными дугами.

Граф G сети Петри есть двудольный ориентированный мультиграф, G = (V, А), где V= {v₁, v₂, ..., v_s} — множество вершин, а А = {a₁, a₂, ..., a_r} — комплект направленных дуг, а_i = (v_j, v_k), где v_j, v_kÎ V. Множество Vможет быть разбито на два непересекающихся подмножества Р и Т, таких, что V = Р U Т, Р I Т = Æ , и для любой направленной дуги a_iÎ А, если a_i= (v_j, v_k), тогда либо v_jÎ Р и v_kÎ T, либо v_jÎ Т, а v_kÎ P.

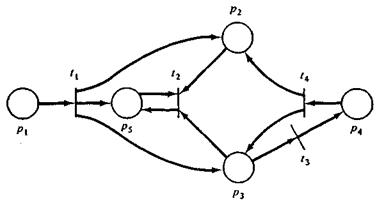
Рис. 1.1. Граф сети Петри

Матричное представление сети Петри.Альтернативным по отношению к определению сети Петри в виде (Р, Т, I, О) является определение двух матриц D^-и D⁺, представляющих входную и выходную функции. Каждая матрица имеет mстрок (по одной на переход) и nстолбцов (по одному на позицию). Определим D^- [j, i]= # (p_i, I(t_j)), a D⁺ [j, i] = #(p_i, 0 (t_j)). D ^-определяет входы в переходы, D⁺— выходы. Матричная форма определения сети Петри (Р, Т, D^-, D⁺) эквивалентна стандартной форме, но позволяет дать определения в терминах векторов и матриц.

Маркировка сетей Петри.Маркировка μ есть присвоение фишек позициям сети Петри. Фишка — это примитивное понятие сетей Петри (подобно позициям и переходам). Фишки присваиваются (можно считать, что они принадлежат) позициям. Количество и положение фишек при выполнении сети Петри могут изменяться. Фишки используются для определения выполнения сети Петри.

Маркировка μ сети Петри С = (Р, Т, I, О) есть функция, отображающая множество позиций Р в множество неотрицательных целых чисел N μ : Р → N. Маркировка μ может быть также определена как вектор μ = (μ ₁, μ₂, … , μ _n), где n = |Р| и каждое μ_iÎ N, i = 1, ..... n. Вектор μ определяет для каждой позиции p_iсети Петри количество фишек в этой позиции. Количество фишек в позиции p_iесть μ_i, i = 1, ..., n.

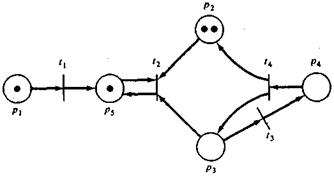
Рис. 1.2. Маркированная сеть Петри

Связь между определениями маркировки как функции и как вектора очевидным образом устанавливается соотношением μ(p_i) = μ_i.

Маркированная сеть Петри М = (С, μ) есть совокупность структуры сети Петри С = (Р, Т, I, О) и маркировки μ и может быть записана в виде М = (Р, Т, I, О, μ). На графе сети Петри фишки изображаются маленькой точкой в кружке, который представляет позицию сети Петри. На рис. 1.2 приведен пример графического представления маркированной сети Петри.

Правила выполнения сетей Петри.Сеть Петри выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции. Переход может запускаться только в том случае, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число фишек, по крайней мере, равное числу дуг из позиции в переход.

Переход t_jÎ Т в маркированной сети Петри С — (Р, Т, I, О) с маркировкой μ разрешен, если для всех p_iÎ Р μ(p_i) ³ #(p_i, I(t_j)).

Переход запускается удалением всех разрешающих фишек из его входных позиций и последующим помещением в каждую из его выходных позиций по одной фишке для каждой дуги. Кратные фишки создаются для кратных выходных дуг. Запуск перехода в целом заменяет маркировку μ сети Петри на новую маркировку μ'. Если какая-либо входная позиция перехода не обладает достаточным количеством фишек, то переход не разрешен и не может быть запущен.

Переход t_jв маркированной сети Петри с маркировкой μ, может быть запущен всякий раз, когда он разрешен. В результате запуска разрешенного перехода t_jобразуется новая маркировка μ', определяемая следующим соотношением: μ'(p_i) = μ(р_i) - #(p_i, I(tj)) + #(р_i, O(t_j)).

В качестве примера рассмотрим маркированную сеть Петри, изображенную на рис. 6.3. При такой маркировке разрешены только три перехода: t₁, t₃и t₄. Переход t₂не разрешен, так как ни позиция р₂, ни позиция р₃, являющиеся входами перехода t₂, не содержат ни одной фишки. Так как переходы t_1,t₃и t₄разрешены, любой из них может быть запущен. Если запущен переход t₄, то происходит удаление фишки из каждого входа и помещение фишки в каждый выход. При этом одна фишка удаляется из р₅, одна фишка помещается в р₃, а количество фишек в р ₄ увеличивается с двух до трех. Новая маркировка, полученная в результате запуска перехода t₄, показана на рис. 1.4.

В маркированной сети Петри, изображенной на рис. 1.4, разрешены только переходы t₁и t₃. При запуске перехода t₁ осуществляется удаление фишки из р₁ и помещение фишек в р₂, р₃ и р₄ (в p₄ — две фишки, так как эта позиция является кратным выходом перехода t₁). Эта операция образует маркировку, приведенную на рис. 1.5.

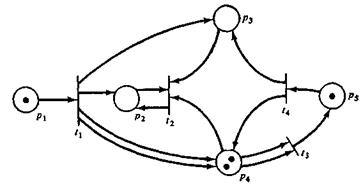
Рис. 1.3. Маркированная сеть Петри для иллюстрации правил запуска. Переходы t₁, t₃ и t₄ разрешены.

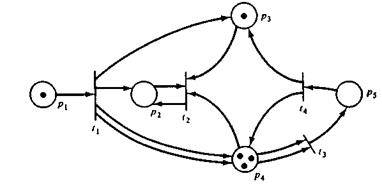
Рис. 1.4. Маркировка, полученная в результате запуска перехода t₄в сети на рис. 1.3.

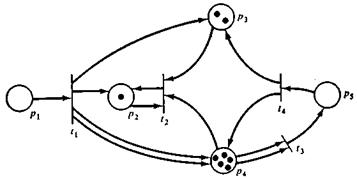
Рис. 1.5. Маркировка, полученная при запуске перехода t₁ в сети на рис. 1.4.

Запуски могут осуществляться до тех пор, пока существует хотя бы один разрешенный переход. Когда не останется ни одного разрешенного перехода, выполнение прекращается.

Пространство состояний сети Петри.Состояние сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети. Пространство состояний сети Петри, обладающей nпозициями, есть множество всех маркировок, т. е. Nⁿ. Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения d , которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке μ (состоянию) и переходу t_j (он должен быть разрешен), она образует новую маркировку (состояние), которая получается при запуске перехода t_jв маркировке μ.

Функция следующего состояния d : NⁿxТ → Nⁿдля сети Петри С = (Р, Т, I, О) с маркировкой μ и переходом t_jÎ Т определена тогда и только тогда, когда μ(p_i) ³ #(p_i, I(t_j)) для всех p_iÎ Р. Если d (μ, t_j) определена, то d (μ, t_j) = μ’, где μ’ (p_i) = μ(p_i) - #(p_i, I(t_j)) + #(p_i, O(t_j)) для всех р_iÎ P.

Пусть дана сеть Петри С = (Р, Т, I, О) с начальной маркировкой μ°. Эта сеть может быть выполнена последовательными запусками переходов. Запуск разрешенного перехода t_jв начальной маркировке образует новую маркировку μ¹ = d (μ°, t_j). В этой новой маркировке можно запустить любой другой разрешенный переход, например t_k, образующий новую маркировку μ² = d (μ¹, t_k). Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.

При выполнении сети Петри получаются две последовательности: последовательность маркировок (μ°, μ¹, μ², ...) и последовательность переходов, которые были запущены (t_j0, t_j1, t_j2, ...). Эти две последовательности связаны следующим соотношением: d (μ^k, t_jk) = μ^k+1 для k = 0,1,2, ... . Имея последовательность переходов μ, легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последовательность переходов, за исключением нескольких вырожденных случаев. Таким образом, обе эти последовательности представляют описание выполнения сети Петри.

Для сети Петри С = (Р, Т, I, О) с маркировкой μ маркировка μ' называется непосредственно достижимой из μ, если существует переход t_jÎ Т, такой, что d (μ, t_j) = μ'.

Можно распространить это понятие на определение множества достижимых маркировок данной маркированной сети Петри. Если μ' непосредственно достижима из μ, а μ" — из μ', говорят, что μ" достижима из μ. Определим множество достижимости R(C, μ) сети Петри С с маркировкой μ как множество всех маркировок, достижимых из μ. Маркировка μ' принадлежит R(С, μ), если существует какая-либо последовательность запусков переходов, изменяющих μ на μ'.

Множество достижимости R(C, μ) для сети Петри С = (Р, Т, I, О) с маркировкой μ есть наименьшее множество маркировок, определенных следующим образом:

1. μ Î R(С, μ);

2. Если μ' Î R(С, μ) и μ" = d (μ', t_j) для некоторого t_jÎ Т, то μ" Î R (С, μ).

Удобно распространить функцию следующего состояния на отображение маркировки и последовательности переходов в новую маркировку. Для последовательности переходов (t_j1, t_j2, ..., t_jk) и маркировки μ маркировка μ’ = d (μ, t_jl, t_j2, ..., t_jk) есть результат запусков: сначала — t_jl, затем — t_j2и т. д. до t_jk. (Такая операция, конечно, возможна только в том случае, если каждый переход к моменту его запуска разрешен.)

Сети Петри для моделирования

Сети Петри были разработаны и используются в основном для моделирования. С их помощью могут быть промоделированы многие системы, в особенности системы с независимыми компонентами, например аппаратное и программное обеспечение ЭВМ, физические системы, социальные и др. Сети Петри применяются для моделирования возникновения различных событий в системе. В частности, сети Петри могут моделировать поток информации или другие ресурсы системы.

Простое представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях. События — это действия, имеющие место в системе. Возникновением событий управляет состояние системы. Состояние системы может быть описано множеством условий. Условие — есть предикат или логическое описание состояния системы. Условие может принимать либо значение «истина», либо значение «ложь».

Так как события являются действиями, то они могут происходить. Для того чтобы событие произошло, необходимо выполнение соответствующих условий. Эти условия называются предусловиями события. Возникновение события может вызвать нарушение предусловий и может привести к выполнению других условий, постусловий.

В качестве примера рассмотрим задачу моделирования простого автомата-продавца. Автомат-продавец находится в состоянии ожидания до тех пор, пока не появится заказ, который он выполняет и посылает на доставку. Условиями для такой системы являются: а) автомат-продавец ждет; б) заказ прибыл и ждет; в) автомат-продавец выполняет заказ; г) заказ выполнен. Событиями будут: 1. Заказ поступил. 2. Автомат-продавец начинает выполнение заказа. 3. Автомат-продавец заканчивает выполнение заказа. 4. Заказ посылается на доставку. Предусловия события 2 (автомат-продавец начинает выполнение заказа) очевидны: (а) автомат-продавец ждет; (б) заказ прибыл и ждет. Постусловие для события 2: (в) автомат-продавец выполняет заказ. Аналогично мы можем определить предусловия и постусловия для всех остальных событий:

События	Предусловия	Постусловия
	нет	б
	а, б	в
	в	г , а
	г	нет

Такое представление системы легко моделировать сетью Петри. В сети Петри условия моделируются позициями, события — переходами. При этом входы перехода являются предусловиями соответствующего события; выходы — постусловиями. Возникновение события равносильно запуску соответствующего перехода. Выполнение условия представляется фишкой в позиции, соответствующей этому условию. Запуск перехода удаляет разрешающие фишки, представляющие выполнение предусловий и образует новые фишки, которые представляют выполнение постусловий.

Сеть Петри на рис. 1.6 иллюстрирует модель приведенного выше автомата-продавца.

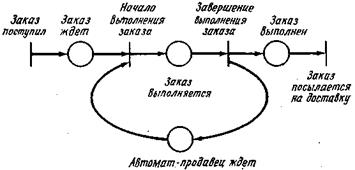
Рис. 1.6. Сеть Петри для простого автомата-продавца

Аналогичный пример можно привести для вычислительной системы, которая обрабатывает задания, поступающие с устройства ввода, и выводит результаты на устройство вывода. Задания поступают на устройство ввода. Когда процессор свободен и в устройстве ввода есть задание, процессор начинает обработку задания. Когда задание выполнено, оно посылается в устройство вывода; процессор же либо продолжает обрабатывать другое задание, если оно имеется, либо ждет прихода задания, если устройство ввода еще не получило такового. Эта система может быть промоделирована сетью Петри, показанной на рис. 1.7.

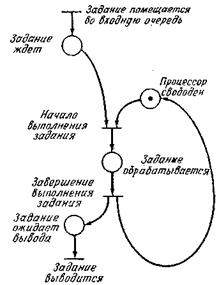
Рис. 1.7. Моделирование простой вычислительной системы

Одновременность и конфликт.Приведенные примеры иллюстрируют некоторые особенности сетей Петри и систем, моделируемых с их помощью. Одной из особенностей является свойственный сетям и их моделям параллелизм, или одновременность. В модели сети Петри два разрешенных невзаимодействующих события могут происходить независимо друг от друга. Синхронизировать события, пока это не потребуется моделируемой системе, нет нужды. Но, когда синхронизация необходима, моделировать ее легко. Таким образом, сети Петри представляются идеальными для моделирования систем с распределенным управлением, в которых несколько процессов выполняются одновременно.

Другая важная особенность сетей Петри — это их асинхронная природа. В сети Петри отсутствует измерение времени или течение времени. Это отражает философский подход к понятию времени, утверждающий, что одно из важнейших свойств времени, с логической точки зрения, — это определение частичного упорядочения событий. В реальной жизни различные события укладываются в различные интервалы времени, и это отражено в модели сети Петри независимостью от времени управления последовательностью событий. Структура сети Петри такова, что содержит в себе всю необходимую информацию для определения возможных последовательностей событий. Таким образом, на рис. 1.7 событие «завершение выполнения задания» должно следовать за соответствующим событием «начало выполнения задания». Однако нет и не требуется никакой информации, связанной с количеством времени, необходимым на выполнение задания.

Выполнение сети Петри (или поведение моделируемой системы) рассматривается здесь как последовательность дискретных событий. Порядок появления событий является одним из возможных, допускаемых основной структурой. Это приводит к явной недетерминированности в выполнении сети Петри, Если в какой-то момент времени разрешено более одного перехода, то любой из нескольких возможных переходов может стать «следующим» запускаемым. Выбор запускаемого перехода осуществляется недетерминированным образом, т. е. случайно. Эта особенность сети Петри отражает тот факт, что в реальной жизненной ситуации, где несколько действий происходит одновременно, возникающий порядок появления событий — не однозначен; скорее может возникнуть любая из множества последовательностей событий. Однако частичный порядок появления события — единственен.

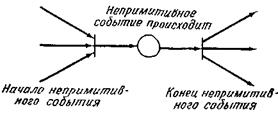
Рис. 1.8. Моделирование" не примитивного события.

Для простоты обычно вводят следующее ограничение. Запуск перехода (и соответствующего события) рассматривается как мгновенное событие, занимающее нулевое время, и возникновение двух событий одновременно невозможно. Моделируемое таким образом событие называется примитивным; примитивные события мгновенны и неодновременны . Непримитивными называются такие события, длительность которых отлична от нуля. Они не являются неодновременными и, следовательно, могут пересекаться во времени. Так как осуществление большинства событий в реальном мире занимает некоторое время, то они являются непримитивными событиями и поэтому не могут должным образом моделироваться переходами в сети Петри. Однако это не приводит к возникновению проблем при моделировании систем. Непримитивное событие может быть представлено в виде двух примитивных событий: «начало непримитивного события», «конец непримитивного события» и условия «непримитивное событие происходит». Эта ситуация может быть промоделирована с помощью сети, показанной на рис. 1.8.

Недетерминированность и неодновременность запусков переходов в моделировании параллельной системы показываются двумя способами. Один из них представлен на рис. 1.9. В этой ситуации два разрешенных перехода в любом случае не влияют друг на друга, и в число возможных последовательностей событий входит последовательность, в которой первым срабатывает один переход, и последовательность, в которой первым будет запущен другой переход. Это называется одновременностью.

Другая ситуация, в которой одновременное выполнение затруднено и которая характеризуется невозможностью одновременного возникновения событий, показана на рис. 1.10. Здесь два разрешенных перехода находятся в конфликте. Может быть запущен только

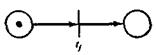
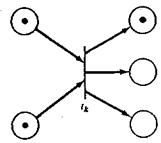
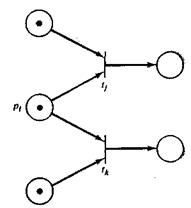
Рис. 1.9. Одновременность. Эти два Рис. 1.10. Конфликт. Переходы t_j,t_k

перехода могут быть запущены находятся в конфликте, т. е. запуск

в любом порядке. одного из них удаляет фишку из p_i

и тем самым запрещает другой.

один переход, так как при запуске он удаляет фишку из общего входа и запрещает другой переход.

Рассмотренные ситуации требуют внимательного изучения моделируемых сетями Петри систем для правильного отображения их поведения.

Анализ сетей Петри