Топологический метод расчета надежности

Метод основан на использовании математического аппарата марковских процессов (вероятность нахождения системы в каком-либо состоянии в будущем не зависит от прошлых состояний системы).

Обозначим Х как множество состояний системы:

,

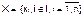где xi – i-е состояние, I – множество индексов всех возможных состояний системы, n – количество возможных состояний системы.

Разобьем множество Х на два подмножества:

- подмножество работоспособных состояний системы Х_р;

- подмножество неработоспособных состояний системы .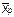

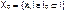
где X_р – подмножество работоспособных состояний системы, I_р – множество индексов работоспособных состояний системы.

,

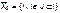где 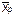– подмножество неработоспособных состояний системы, J – множество индексов неработоспособных состояний системы.

Нахождение системы в том или ином состоянии обусловливает случайный процесс X(t)перехода системы в пространстве ее состояний. X(t) называют также траекторией системы.

Представим X(t) в виде вероятностного графа состояний G(X, W), где Х – множество вершин графа, соответствующих множеству состояний X; W – множество дуг, соединяющих вершины данного графа; P₁(t), ..., P_i(t), ..., P₆(t) – вероятности нахождения системы в i-м состоянии; d(w_ij) – вес дуги w_ij; a_ij – интенсивность перехода из состояния i в состояние j(рис. 2.6).

Если заданы интенсивности a_ij, то, составляя и решая систему уравнений Колмогорова, можно определить вероятности нахождения системы в i-м состоянии P_i(t), а значит и показатели надежности. Однако составление и решение системы уравнений Колмогорова является трудоемкой операцией, поэтому для решения подобных задач применяют топологический метод.

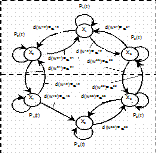
Рис. 2.6. Пример вероятностного графа состояний G(X,W)

Топологический метод использует аппарат теории графов применительно к решению задач надежности. Рассмотрим методику решения задач методом, который позволяет непосредственно по графу состояний G(X, W) без составления и решения уравнений Колмогорова вычислять показатели надежности. Для этого введем некоторые определения.

19 Прямой путь l^ij из вершины х_i в вершину х_j – цепь последовательно соединенных однонаправленных дуг, где каждая вершина имеет входящую и одну выходящую дуги, за исключением начальной и конечной, имеющих по одной дуге (рис. 2.7).

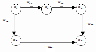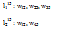Рис. 2.7. Определение прямых путей на графе

Вес k-го прямого пути из вершины i в вершину j

,

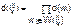где 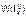- множество дуг, которые составляют k-ый прямой путь.

Замкнутый контурr – прямой путь, на котором начальная и конечная вершины совпадают (рис. 2.8). Вес замкнутого контура r

,

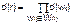где 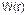– множество дуг, входящих в замкнутый контур r.

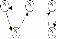Рис. 2.8. Примеры замкнутых контуров

Частным случаем замкнутого контура является петля (рис. 2.9), в которой входящая и выходящие дуги сливаются в одну.

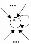
Рис. 2.9. Петля

Вес петли при вершине определяется как отрицательная сумма весов дуг, исходящих из этой петли:

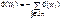
где J_n – множество индексов вершин, которые связаны с i-ой вершиной выходящими из нее дугами.

Соединение графа S – это частичный граф, который образуют только замкнутые контуры. Частичный граф представляет собой все вершины, некоторые дуги и петли исходного графа, которые составляют независимые замкнутые контуры (то есть контуры, не имеющие общих вершин). Один граф может располагать несколькими соединениями (рис. 2.10). При образовании соединений следует помнить, что каждая вершина графа G (X, W) имеет петлю.

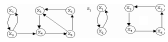Рис. 2.10. Пример образования соединения графа

Вес j-го соединения

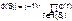
где n – число независимых замкнутых контуров, образующих соединение, R(S_j) – множество независимых замкнутых контуров, образующих соединение.

Определитель графа

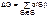
где S — множество всех возможных соединений графа.

20 Теперь рассмотрим методику расчета показателей надежности топологическим методом в установившемся режиме, где топологические коэффициенты С_i для каждой x_i вершины графа определяются непосредственно по графу, а затем вычисляется нужный показатель по ниже приведенным топологическим формулам.

Для определения коэффициента С_i необходимо:

– выбрать начальную вершину графа x_q отдельно для определения каждого из коэффициентов С_i ( 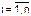); начальная вершина может быть выбрана произвольно, однако выбор влияет на объем вычислений, поэтому ее надо выбирать так, чтобы были длинные прямые пути;

– построить множество К прямых путей из начальной вершины x_q в вершину x_i, для которой определяется коэффициент;

– для каждого k-го прямого пути построить множество замкнутых контуров подграфа G{X_k} и образовать возможные комбинации независимых замкнутых контуров (множество соединений S), где G{X_k} – подграф графа G{X, W}, образованный удалением множества вершин, входящих в k-й путь и прилегающих к нему дуг;

– записать коэффициенты C_i по найденным составляющим по формуле

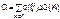
гдe К – множество прямых путей из произвольно выбранной вершины х_q в х_i; Х_к - множество вершин, входящих в k-ый прямой путь.

Используя топологические коэффициенты, основные показатели надежности установившегося режима можно записать:

– вероятность нахождения системы в i-м состоянии

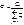
где n – число вершин графа;

– коэффициент готовности

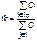
где I_p – множество индексов работоспособных состояний системы;

– коэффициент простоя

,

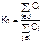где J – множество индексов неработоспособных состояний системы;

– среднюю наработку на отказ

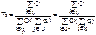
где 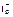– подмножество индексов граничных состояний из X_р, из которых в неработоспособное состояние можно попасть за один переход;

– среднее время восстановления

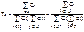
где J⁺ – подмножество индексов граничных состояний из 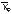, из которых в работоспособное состояние можно попасть за один переход.

Основные положения топологического метода могут быть применены для определения показателей надежности неустановившегося режима с использованием преобразований Лапласа.