Суждение как форма мышления
(ПОНЯТИЕ О СУЖДЕНИИ)
Суждение — это форма мышления, представляющая собой утверждение или отрицание существования предметов и явлений, связей между предметами и их свойствами или об отношениях между предметами. Суждение может быть истинным или ложным и выражается в языке, как правило, с помощью повествовательных предложений.
В суждении выделяют предмет, или субъект (который принято обозначать латинской буквой S) и предикат (обозначается латинской буквой Р), а также связку, выражаемую словами «есть», «суть» (утвердительная связка) или «не есть», «не суть» (отрицательная связка), а также их синонимическими им словами. Простейшую форму суждения можно выразить следующим образом:
а) (S есть Р) — форма утвердительного суждения;
б) (S не есть Р) — форма отрицательного суждения.
Различают простые суждения («Иванов — юрист»; «Иванов любит музыку») и сложные суждения («Иванов — юрист и любит музыку»).
Простое суждение содержит одно утверждение либо одно отрицание. Сложное суждение состоит из двух или большего числа простых суждений, соединенных особыми логическими союзами (пропозициональными связками), которые в языке выражаются словами: «и» — конъюнкция, «или» и «либо» — нестрогая и строгая дизъюнкция и т.д.
Как простые, так и сложные суждения имеют два основных значения истинности — «истинно» (в дальнейшем будет обозначаться буквой И) и «ложно» (буквой Л). Истинность базисных простых суждений устанавливается обращением к соответствующим предметам непосредственно. Истинность сложных суждений зависит от истинности простых суждений и логических союзов (пропозициональных связок), которые в них используются, а также от операции отрицания, о чем пойдет речь ниже.
Истинным суждением является суждение, которое соответствует действительности: «Москва — столица России». Суждение «Киев — столица Белоруссии» ложное суждение, т.к. оно действительности не соответствует.
Глава 2.
СОСТАВ ПРОСТОГО СУЖДЕНИЯ
И ЕГО ВИДЫ
Простыми суждениями называются суждения, которые содержат в себе лишь один субъект и один предикат, одно утверждение или одно отрицание.
Различают несколько типов простых суждений. По характеру признаков, которые утверждаются или отрицаются относительно субъектов (предметов мысли) простые суждения подразделяются на:
а) атрибутивные, или суждения о свойствах — это суждения, в которых утверждается или отрицается наличие признаков-свойств (атрибутов) у субъектов. Признаки-свойства характеризуют предметы сами по себе, вне связи с другими предметами: цвет, форма, вес, плотность и т.п.
б) релятивные, или суждения об отношениях — это суждения, в которых утверждается или отрицается наличие у каких-либо предметов (не менее двух) признаков-отношений. Такие признаки характеризуют предметы со стороны их отношений, взаимодействий, связей с другими предметами: «выше», «ниже», «родство» и т.п.
в) экзистенциальные суждения, или суждения существования — это суждения, в которых утверждается или отрицается существование или несуществование предметов, явлений, например: «Существует социальная демократия»; «Идеальных законов не бывает». В суждениях существования речь идет не о признаках предметов как таковых; в них утверждается или отрицается само наличие предметов. Такие суждения составляют основу всех наших рассуждений, так как прежде, чем выяснять признаки предметов, следует установить само существование этих предметов.
Если перейти к более формальному анализу простых суждений, то здесь следует рассмотреть традиционное подразделение всех, прежде всего атрибутивных суждений по количеству и по качеству. При этом учитывается наличие четырех основных элементов логической формы простого суждения: субъекта, предиката, связки (утвердительной или отрицательной) и квантора. О первых трех говорилось в самом начале раздела. Введем понятие «квантор».
Квантором называется количественная, связанная с объемом характеристика субъекта простого суждения в его отношении к предикату.
Атрибутивные суждения, у которых точно установлены количественная и качественная характеристики, называются простыми категорическими суждениями.
В зависимости от связки различают:
а)утвердительные простые категорические суждения и
б) отрицательные простые категорические суждения.
В зависимости от особенностей квантора, то есть количественной характеристики субъекта по отношению к предикату, различают:
а) общиепростые категорические суждения, в которых речь идет обо всех предметах, мыслимых в субъекте по отношению к признаку, выраженному предикатом, например: «Все цветы прекрасны». Форма таких суждений — «Все S суть (не суть) Р». Здесь квантор выражен словом «все», это квантор общности.
б) частные простые категорические суждения — суждения, в которых нечто высказывается только о части предметов, выраженных субъектом, которые обладают или не обладают некоторым признаком, например: «Некоторые студенты не сдали экзаменов». Форма таких суждений — «Некоторые S не суть (суть) Р». Здесь квантор выражен словом «некоторые», это квантор существования.
в) единичные простые категорические суждения, в которых речь идет об отдельно взятых индивидуальных предметах, например: «Александр Македонский — выдающийся полководец». Форму таких суждений можно выразить примерно следующим образом — «Тот самый S есть (не есть) Р».
Если, далее, объединить оба приведенные выше подразделения простых категорических суждений — по качеству (связка) и количеству (квантор), то мы получаем следующие виды этих суждений: 1) общеутвердительные, 2) общеотрицательные, 3) частноутвердительные, 4) частноотрицательные, 5) единичные утвердительные и 6) единичные отрицательные суждения.
Отношения между субъектами и предикатами всех видов простых категорических суждений можно выразить с помощью кругов Эйлера, в виде круговых схем. Объем единичного понятия будем обозначать точкой или звездочкой, или же маленьким кружочком — логический класс, состоящий из одного элемента. (см. Рис. 10).

Рис. 11
Общий анализ видов простых категорических суждений ограничивают обычно только первыми четырьмя разновидностями, так с точки зрения логической формы единичные суждения ведут себя как общие суждения соответствующего качества: единичные утвердительные — как общеутвердительные. Единичные отрицательные — как общеотрицательные, что также можно видеть по рисунку 11.
В традиционной логике принято обозначать различные категории простых категорических суждений латинскими прописными буквами, взятыми из латинских слов «afirmo» — «утверждаю» и «nego» — «отрицаю». При этом, общеутвердительные суждения обозначаются буквой А, частноотрицательные — буквой I, взятыми из слова «afirmo»; общеотрицательные — буквой Е, частноотрицательные — буквой О, взятыми из слова «nego». Это также отражено в таблице на рисунке 11.
Заметим также, что субъект и предикат простого категорического суждения называются его терминами, которые могут быть распределены или нераспределены, в зависимости от используемого в суждении квантора — общности или существования. Распределенным называется термин, который по отношению к другому термину (S по отношению к Р, Р по отношению к S) формально берется в полном объеме, т.е. либо полностью включается, либо полностью исключается, либо полностью совпадает с ним. Нераспределенным называется термин, который по отношению к другому берется не в полном объеме, а частично, частично включается или частично исключается из него. Для единичных суждений распределенность субъекта гарантирована тем, что он представляет собой единичное понятие. Кстати, введем также и для единичных суждений буквенные обозначения, а именно: для единичных утвердительных — Ае, так как они ведут себя формально как общеутвердительные, для единичных отрицательных — Ее, так как они ведут себя формально подобно общеотрицательным суждениям.
Будем обозначать распределенность термина знаком «плюс» (+), нераспределенность — знаком «минус» (–), что также отражено на рис. 10.
Распределенность терминов простых категорических суждений легко представить с помощью небольшой таблички (см. Рис. 12), в которой учтены также особенности еще двух разновидностей простых категорических суждений — общевыделяющих (обозначим их — Ав) и частновыделяющих (обозначим их — Iе).
| А | Е | I | О | Ае | Ее | Ав | Iв | |
| S | + | + | – | – | + | + | + | – |
| Р | – | + | – | + | – | + | + | + |
Рис. 12
Общевыделяющими называются такие общие простые категорические суждения, в которых субъект и предикат по объему полностью совпадают, оказываются в отношении равнозначности или тождества. Их форму можно представить следующим образом — «Все S, и только эти S, суть Р». В общевыделяющих суждениях распределены как субъекты, так и предикаты. В частновыделяющем утвердительном суждении (форма — «Некоторые S, но только эти S, суть Р») часть элементов субъекта составляют весь объем предиката, который поэтому оказывается распределенным термином. Круговые схемы этих суждений, а также распределенность их терминов можно видеть на Рис. 13.
Общевыделяющие и частновыделяющие суждения позволяют делать из них более сильные выводы, чем из простых общеутвердительных и частноутвердительных суждений.
Ав Iв
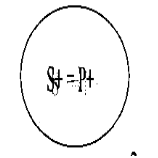
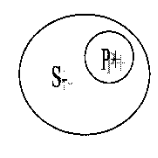
Рис. 13
Глава 3.
СЛОЖНОЕ СУЖДЕНИЕ
И ЕГО ВИДЫ
Сложные суждения — это суждения, которые состоят из двух или большего числа простых суждений, единичных утверждений или отрицаний, соединенных особыми логическими союзами (пропозициональными связками). Следует обратить внимание на то обстоятельство, что между простыми и сложными суждениями существуют своеобразные переходные формы — то т.н. простые суждения со сложными субъектами или сложными предикатами.
Простыми суждениями со сложными субъектамиявляются суждения, у которых имеется один предикат и субъект, состоящий из двух или более различных частей, каждая из которых может считаться самостоятельным субъектом, например: «Петров и Иванов являются студентами-юристами». Форма такого суждения следующая:
(S1 и S2 суть Р)
Простыми суждениями со сложными предикатами являются суждения, у которых имеется один субъект и предикат, состоящий из двух частей, каждая из которых может считаться самостоятельным предикатом, например: «Петров является студентом и занимается спортом». Форма такого суждения следующая:
(S есть Р1 и Р2)
Истинность таких суждений зависит от того, обладают ли признаком Р оба субъекта S1 и S2 —для первых; и обладает ли субъектS признаками, заключенными в обоих предикатах Р1 иР2 — для вторых. Считается, что в случае простых суждений со сложными субъектами или сложными предикатами имеют место сложные суждения, взятые в сокращенной форме. Полная форма таких суждений может быть записана следующим образом:
(S1 есть Р) и (S2 есть Р) — для первых,
(S есть Р1) и (S есть Р2) — для вторых.
К числу основных логических союзов (пропозициональных связок), с помощью которых из простых образуются сложные суждения, а также из одних сложных суждений образуются еще более сложные, относятся союзы, которые выражаются в обычном языке выражаются словами: «и», «или», «либо», «если… , то», «если и только если», а также синонимичными им выражениями.
«И» — конъюнкция, или соединительный союз;
«ИЛИ» — слабая дизъюнкция, или слабый разделительный союз;
«ЛИБО» («ИЛИ… ИЛИ») — строгая дизъюнкция, или строго разделительный союз;
«ЕСЛИ… , ТО» — импликация, или условный союз;
«ЕСЛИ И ТОЛЬКО ЕСЛИ» («ТОГДА И ТОЛЬКО ТОГДА, КОГДА») — эквивалентность.
В сводном виде информация о союзах представлена в таблице на Рис.14.

Рис. 14
Примечание: для обозначения тех или иных союзов иногда используются символы, отличные от тех, которые даны на Рис. 14.
Кроме союзов, в образовании сложных суждений важную роль играет операция отрицания суждений. Операция отрицания суждений в языке выражается словами «НЕТ», «НЕВЕРНО, ЧТО» и некоторыми другими. В языке современной логики ее зачастую изображают черточкой (чертой) на символом (формулой) суждения, или символом (). В данном пособии в силу технических обстоятельств применяются оба способа символического изображения отрицания. Так, отрицание простого суждения можно изобразить следующим образом: (А),читается как«не-А», или «неверно, что А».
Содержательная характеристика логических союзов и операции отрицания, связанная с истинностью суждений, вводится с помощью так называемых таблиц истинности сложных суждений (см. Рис. 15). Эти таблицы рассматриваются также в качестве особых табличных определений логических союзов и операции отрицания.
| А | В | А^В | АvВ | А  В В | А→В | А↔В | А | В | (А→В)→(В→А) | |||
| И | И | И | И | Л | И | И | Л | Л | (А→В) | (В→А) | ||
| 1 3 2 | 4 6 5 | |||||||||||
| и И и | И | л И л | ||||||||||
| И | Л | Л | И | И | Л | Л | Л | И | и Л л | И | и Л л | |
| Л | И | Л | И | И | И | Л | И | Л | л И и | И | л И и | |
| Л | Л | Л | Л | Л | И | И | И | И | л И л | И | и И и |
Рис. 15
В таблице на Рис. 15 простые суждения обозначены первыми заглавными буквами латинского алфавита, символы даны согласно Рис. 14, за исключением операции отрицания, что было оговорено выше.
Опираясь на Рис. 15 можно дать следующие развернутые определения логических союзов и операции отрицания:
Конъюнкция — это логический союз, с помощью которого из двух или большего числа исходных суждений образуется новое суждение (конъюнктивное суждение, или просто конъюнкция), которое истинно тогда и только тогда, когда истинны все исходные суждения, и ложно во всех остальных случаях.
В таблице (Рис. 15) на это указывают значения в четвертом столбце. Истинной является конъюнкция только в первой строке столбца. Сама таблица строится следующим образом: в первом столбце пронумерованы строки, которых для рассматриваемых случаев достаточно четырех. Это связано с количеством простых суждений, входящих в состав сложного. В общем случае число строк в таблице определяется по формуле 2ⁿ, где n — число разных простых суждений, сколько бы раз каждое из них не повторялось в составе сложного суждения. Если простых суждений 2, что число строк — 2² = 4.
Далее, в столбцах 4–8 даны все возможные истинностные значения для соответствующих союзов, соединяющих только по два простых суждения, взятых без операции отрицания.
В 9-м и 10-м столбцах приведены значения для отрицания простых суждений А и В по отдельности.
Наконец, в 11-м столбце приведены значения для более сложного, чем 4–8, случая, в котором сложное суждение образуется из двух других, каждое из которых также является сложным суждением, и при этом во втором из них дважды применяется операция отрицания.
Слабая, или нестрого разделительная дизъюнкция — это логический союз, с помощью которого из двух или большего числа исходных суждений образуется новое сложное суждения (дизъюнктивное, или просто дизъюнкция), которое истинно во всех случаях, когда истинно хотя бы одно из исходных суждений, и ложно, когда ложны все исходные суждения. В таблице на Рис. 15 на ложность слабой дизъюнкции указывает значение «Л» в четвертой строке пятого столбца, для случая, когда А и В имеют одновременно также значение «Л».
Сильная, или строго разделительная дизъюнкция — это логический союз, с помощью которого также из двух или большего числа исходных образуется новое сложное суждение (строгая дизъюнкция), которое истинно тогда и только тогда, когда истинно лишь одно из всех исходных суждений, и ложно во всех остальных случаях. В таблице на Рис. 15 это представлено столбцом 6. В нем значение «И» имеет место во 2-й и 3-й строках, когда A и B имеют разные значения, а значение «Л» — в 1-й и 4-й строках, когда A и B имеют одинаковые значения: «ИИ» и «ЛЛ», соответственно.
Относительно импликации и эквивалентности, прежде чем давать их табличные определения, следует сделать оговорку. С помощью этих союзов новое суждение всегда образуется из двух исходных, которые, правда, в свою очередь, могут быть простыми или сложными. Первые члены импликативных и эквивалентных суждений называются антецедентами, или предшествующими членами, вторые — консеквентами, или последующими членами.
Импликация —это логический союз, с помощью которого из двух простых или сложных суждений образуется новое, которое истинно во всех случаях, кроме одного, а именно, оно ложно, когда истинен первый член (антецедент), а второй (концеквент) имеет значение «Л». Иначе говоря, из истины не может следовать ложное суждение.
С импликацией связана определённая трудность для обычного, содержательного понимания связи «Если…, то…». С помощью этого союза содержательно чаще всего выражают связь причины и следствия, условия и некоторого результата, или действия. Поэтому содержательно не очень понятно, почему в 3-й и 4-й строках импликацию нужно считать истинной. Эти случаи даже получили особое название — «парадоксы материальной импликации», то есть содержательной. Не вдаваясь в детали, скажем, что здесь мы имеем дело с формальным союзом «Если…, то…», который распространяется на все четыре возможных варианта соединения значений истинности для двух суждений, взятых со стороны их формы.
Весь имеющийся опыт использования импликации говорит в пользу того, что в этих строках импликативное суждение нужно считать истинным. Хотя в обычном опыте мы имеем дело всегда с содержательными случаями, подпадающими под значение первых двух строк таблицы для импликации. Достаточно сказать, что так ведут себя все известные технические схемы, которые моделируют связь «Если…, то…». В современной логике для того, чтобы уловить все оттенки содержательного (материального) значения союза «Если…, то…», разрабатываются специальные формальные варианты, например, так называемой «сильной импликации».
Эквивалентность — это логический союз, с помощью которого образуется новое суждение, всегда из двух исходных, которое истинно тогда, когда оба входящие в него суждения (антецедент и консеквент) имеют одинаковые значения истинности, то есть оба имеют значение «И» или оба имеют значение «Л». И ложное — когда антецедент и консеквент имеют разные значения: строки 3 и 4 в таблице, 8-й столбец (Рис. 15). Следует обратить внимание на соответствующие значения эквивалентности и строгой дизъюнкции: они имеют для всех строк (столбцы 6 и 8 Рис. 15) разные значения — там, где дизъюнкция строгая даёт «И» — там эквивалентность даёт «Л», и наоборот. Поэтому данные союзы называют иногда «антиэквивалентностью» и «антидизъюнкцией», соответственно.
Отрицание — это логическая операция, с помощью которой образуется новое суждение (отрицание первого), истинное, когда исходное имеет значение «Л», и ложное когда исходное имеет значение «И». В столбцах 9 и 10 (Рис. 15) даны результаты отрицания простых суждений A и B. С операцией отрицания связан интересный закон — закон двойного (или чётного) отрицания. Этот закон гласит: двойное отрицание (любое четное число отрицаний) суждения образует суждение, истинность которого совпадает с истинностью исходного суждения. Этот закон говорит также о том, что одно или нечетное число отрицаний одного и того же суждения образует суждение, значение которого противоположно значению исходного отрицаемого суждения. В реальной жизни со многими отрицаниями мы сталкиваемся, например, в ситуациях дачи многократных показаний, либо одним и тем же человеком, либо разными людьми по поводу высказываний (суждений) других людей. В первом случае имеет место противоречие самому себе, во втором случае — противоречие с показаниями опрошенных ранее.
В 11-м столбце таблицы на Рис. 15 приведены истинностные значения сложного суждения, у которого части в свою очередь представляют собой сложные суждения. Составление таблиц для форм сложных суждений со сложными частями происходит в определённом порядке, как, например, действия в сложных арифметических и алгебраических выражениях. Суть этого порядка заключается в том, что выясняется последовательность, в которой образуются истинностные значения исходных и более сложных частей. Исходным уровнем здесь являются истинностные значения простых суждений, взятых без отрицания. Затем учитывается отрицание простых суждений (значения истинности при этом меняются на противоположные). Затем устанавливается истинность сложных частей, состоящих из двух простых, или большего числа — для конъюнкции, дизъюнкции и строгой дизъюнкции, как с отрицанием, так и без них, которые образуют самостоятельные члены сложного суждения, о чем говорят одинарные скобки. Затем устанавливается истинностное значение выражений следующего уровня (двойные скобки) и т.д. Если нужно — учитывается отрицание сложных суждений, то есть когда отрицание относится ко всему сложному выражению, стоящему в одинарных, двойных и т.д. скобках.
Для выражения, взятого в 11-м столбце на Рис. 15, построение таблицы истинности заключается в следующем:
1) устанавливаются значения A и B (берутся из столбцов 2 и 3);
2) устанавливаются значения для отрицаний A и B (столбцы 9 и 10) соответственно;
3) устанавливается значение правой скобки — (А → В) (можно взять из столбца 7 для импликации двух утвердительных суждений A и B);
4) устанавливается значение истинности для правой скобки путем применения определения импликации — (В → А) («Л», когда антецедент «И», а консеквент «Л»);
5) наконец, также по определению импликации, устанавливается истинность всего выражения на основании знания значений истинности левой и правой скобок на основе все того же общего определения истинности для операции импликации.
В итоге обнаруживается интересный случай — мы получили форму суждения, для которой во всех возможных четырех случаях имеет место значение «И». Такие формы называются тождественно-истинными формами.Эти формы выражают логические законы, или правила вывода. Данный закон (правило) говорит о том, что правая и левая скобки, точнее суждения, с формами, стоящими в этих скобках, всегда имеют такие значения истинности, которые сохраняют истинность всего выражения. В подобных суждениях левую часть можно всегда заменить на правую, т.к. они находятся в отношении эквивалентности.
Рассмотренные выше определения логических союзов (пропозициональных связок) и операции отрицания могут быть использованы для формального определения условий истинности любого сложного суждения, коль скоро выявлена его логическая форма. Эти определения также используются для определения параметров сложных схем, например, электрических, формальная структура которых аналогична структуре соответствующих сложных суждений (см. раздел I, глава 3 о теоретическом и практическом значении логики).
На основе формальных и содержательных (истинностных) особенностей простых и сложных суждений различных видов в следующем — пятом — разделе будут рассмотрены особенности различных видов умозаключений, в которых суждения выполняют функции посылок и заключений.
Глава 4.
