Установка ум 11м. устройство и принцип работы
Таблица 1.2
| № набора | x1 | x0 | y |
Запишем обобщенную форму СДНФ для этой функции и одновременно уравнение для MS 4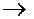 1:
1:
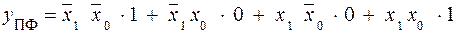 (1.8)
(1.8)
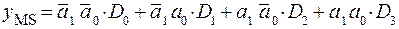 (1.9)
(1.9)
Очевидно полное совпадение выражений (1.8) и (1.9), из которых следует, что если логические переменные х1 и х0 подать на соответствующие адресные входы a1 и a0 MS 4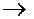 1, то на его информационные входы D0, D1, D2 и D3 нужно подать соответственно 1, 0, 0 и 1 (см. рис. 1.8).
1, то на его информационные входы D0, D1, D2 и D3 нужно подать соответственно 1, 0, 0 и 1 (см. рис. 1.8).
В общем случае можно сформулировать следующее правило: если количество логических переменных n, от которых зависит реализуемая ФАЛ, совпадает с разрядностью адресной части мультиплексора, то эти переменные подаются на адресные входы мультиплексора (старшая переменная - на старший адресный вход), а на информационные входы мультиплексора MS 2n 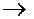 1 – константы 0 и 1 в соответствии с таблицей истинности реализуемой ФАЛ.
1 – константы 0 и 1 в соответствии с таблицей истинности реализуемой ФАЛ.
Рис. 1.8. Реализация ПФ yMS на мультиплексоре
Попробуем реализовать теперь ПФ, зависящую от трех переменных (см. табл. 1.3), на том же MS 4 1.
1.
Таблица 1.3
| № набора | x2 | x1 | x0 | y |
Запишем минимальную дизъюнктивную нормальную форму (МДНФ) для этой ПФ, воспользовавшись картой Вейча, представленной на рис. 1.9.
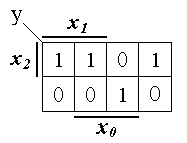
Рис. 1.9. Карта Вейча для ПФ y (табл. 1.3)
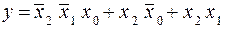 (1.10)
(1.10)
Преобразуем выражение (1.10) к виду, аналогичному выражению (1.8):
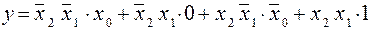 , (1.11)
, (1.11)
где произведение 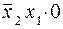 введено для того, чтобы в выражении (1.11) были представлены все четыре конституенты единицы двух переменных х2 и х1.
введено для того, чтобы в выражении (1.11) были представлены все четыре конституенты единицы двух переменных х2 и х1.
Если сравнить выражения (1.11) и (1.9), то можно заметить их полное соответствие. Отсюда видно, что две логические переменные х2 и х1 нужно подать соответственно на адресные входы a1 и a0 MS 4 1, а информационные входы D0, D1, D2 и D3 для произвольной ФАЛ, зависящей от трех переменных, в общем случае являются функциями от третьей переменной х0. Такими функциями являются:
1, а информационные входы D0, D1, D2 и D3 для произвольной ФАЛ, зависящей от трех переменных, в общем случае являются функциями от третьей переменной х0. Такими функциями являются: 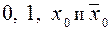 . Реализация данной ПФ представлена на рис. 1.10.
. Реализация данной ПФ представлена на рис. 1.10.
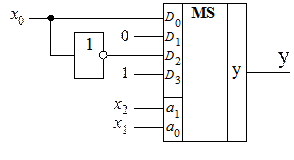
Рис. 1.10. Реализация ПФ 3 аргументов на MS 4 1
1
Тот же результат можно получить, если в табл. 1.3 выделить четыре группы по две строки в каждой и отделить переменную х0 от х2 и х1 (см. табл. 1.4, где выделения сделаны жирными линиями).
| № набора | x2 | x1 | x0 | y |
Из табл. 1.4 видно, что переменные х2 и х1 образуют четыре набора, на каждом из которых функция y зависит только от одной переменной х0, причем значения y = f(х0) легко выявляются из этой таблицы.
Таблица 1.4
Для общего случая можно сформулировать следующее правило:
если количество логических переменных n, от которых зависит реализуемая ПФ, на единицу больше разрядности адресной части мультиплексора, то данную ПФ можно реализовать на мультиплексоре MS 2n  1 и одном инверторе.
1 и одном инверторе.
Если распространить данный метод на реализацию ПФ, зависящей от четырех переменных, на том же MS 4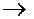 1, то, очевидно, что если две старшие переменные х3 и х2 подать соответственно на адресные входы a1 и a0, то информационные входы будут функциями двух младших переменных х1 и х0. Всего таких функций 16, из них шесть – вырожденные (0, 1,
1, то, очевидно, что если две старшие переменные х3 и х2 подать соответственно на адресные входы a1 и a0, то информационные входы будут функциями двух младших переменных х1 и х0. Всего таких функций 16, из них шесть – вырожденные (0, 1, 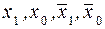 ), а 10 функций зависят от двух переменных, причем для реализации последних требуются восемь различных логических элементов (И, И-НЕ, ИЛИ, ИЛИ-НЕ,
), а 10 функций зависят от двух переменных, причем для реализации последних требуются восемь различных логических элементов (И, И-НЕ, ИЛИ, ИЛИ-НЕ, 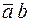 – элемент запрета,
– элемент запрета, 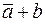 –элемент, реализующий функцию импликации,
–элемент, реализующий функцию импликации, 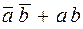 –элемент равнозначности и
–элемент равнозначности и 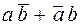 –элемент, реализующий сумму по модулю два).
–элемент, реализующий сумму по модулю два).
Итак, данная реализация потребует кроме мультиплексора, в худшем случае, восемь различных логических элементов, поэтому ее, как правило, не рекомендуется использовать на практике.
В некоторых частных случаях ПФ, зависящую от четырех переменных, можно реализовать с использованием только одного мультиплексора MS 4 1 без каких либо логических элементов. Рассмотрим эти случаи. Пусть требуется реализовать ПФ, представленную картой Вейча (см. рис. 1.11).
1 без каких либо логических элементов. Рассмотрим эти случаи. Пусть требуется реализовать ПФ, представленную картой Вейча (см. рис. 1.11).
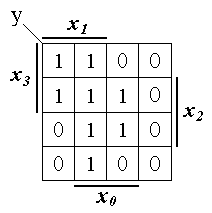
Рис. 1.11. Задание ПФ на карте Вейча
Если две старшие переменные х3 и х2 подать на адресные входы a1 и a0 MS 4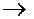 1, то информационные входы D0, D1, D2 и D3 можно представить четырьмя картами Вейча для двух переменных х1 и х0 (см. рис. 1.12). Эти карты являются в данном случае строками карты Вейча, представленной на рис. 1.11.
1, то информационные входы D0, D1, D2 и D3 можно представить четырьмя картами Вейча для двух переменных х1 и х0 (см. рис. 1.12). Эти карты являются в данном случае строками карты Вейча, представленной на рис. 1.11.
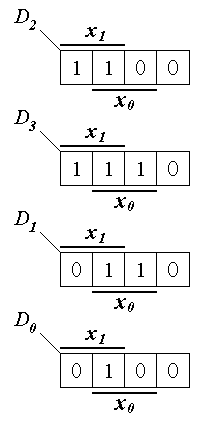
Рис. 1.12. Строки карты Вейча
Из рис. 1.12 следует: D0 = х1 х0, D1 = х0, D2 = х1 + х0 и D3 = х1.
Соответствующая схемная реализация представлена на рис. 1.13.
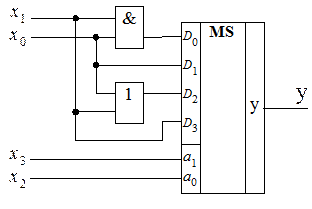
Рис. 1.13. Схемная реализация ПФ (рис. 1.11)
Подадим теперь на адресные входы a1 и a0 соответственно переменные х1 и х0, тогда информационные входы D0, D1, D2 и D3 можно представить четырьмя картами Вейча для двух переменных х3 и х2 (см. рис. 1.14), причем эти карты являются в данном случае столбцами карты Вейча, представленной на рис. 1.12.
Рис. 1.14.Столбцы карты Вейча
Из рис. 1.15 следует, что D0 = 0, D1= х2, D2 = 1 и D3 = х3. Соответствующая реализация представлена на рис. 1.15.
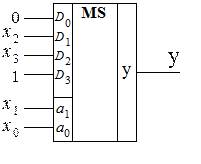
Рис. 1.15. Схемная реализация ПФ (рис. 1.11)
Сравнивая рис. 1.13 и рис. 1.15, делаем очевидный вывод о предпочтительности реализации, представленной на рис. 1.15, так как здесь не требуется никаких логических элементов.
Поиск рациональной структуры по данной методике в общем случае потребует анализа шести вариантов подачи двух различных переменных из четырех на адресные входы MS 4 1 (здесь шесть - это число различных сочетаний из четырех переменных по две). Проще рациональную структуру выявить, выполняя следующие процедуры.
1 (здесь шесть - это число различных сочетаний из четырех переменных по две). Проще рациональную структуру выявить, выполняя следующие процедуры.
Записать реализуемую ПФ в МДНФ. В нашем случае из рис. 1.11 следует:
 (1.12)
(1.12)
Определить две переменные, наиболее часто встречающиеся в различных простых импликантах. В нашем случае это переменные х1 и х0, так как они встречаются по два раза, а переменные х3 и х2 только один раз. Именно переменные х1 и х0 необходимо подать на соответствующие адресные входы a1 и a0 MS 4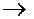 1.
1.
Используя правило развертывания, законы дополнительности, одинарных элементов, поглощения и распределительный закон первого рода, преобразовать МДНФ к виду, когда в выражении для реализуемой ФАЛ присутствуют все четыре конституенты единицы двух переменных, выявленных на предыдущей процедуре. В нашем случае имеем:
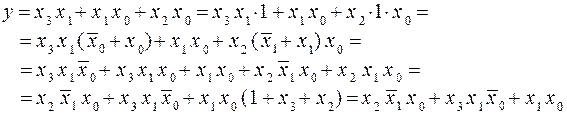 (1.13)
(1.13)
Представим теперь выражение (1.13) в виде, аналогичном выражению (1.8):
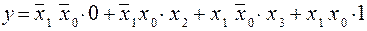 (1.14)
(1.14)
Сравнивая выражения (1.9) и (1.14), выявляем, что D0 = 0, D1= х2, D2 = х3 и D3 =1 (см. рис. 1.15). Эту методику можно распространить и на реализацию систем двух или четырех ПФ с использованием двух- или четырехразрядных мультиплексоров, имеющих общую адресную часть. Рациональный выбор переменных, подаваемых на адресные входы мультиплексоров, определяются подсчетом общего числа каждой переменной, входящей в две или четыре функции, и в качестве адресных выбираются те переменные, которые встречаются наибольшее число раз во всех простых импликантах всех реализуемых ФАЛ.
Если использовать стробируемые MS 2n 1, имеющие три состояния выхода, то любую ФАЛ, зависящую от n+ 2 переменных, легко реализовать на двух стробируемых мультиплексорах и двух инверторах. Один из инверторов используется в цепи стробирования одного из мультиплексоров, а другой на их информационных входах.
1, имеющие три состояния выхода, то любую ФАЛ, зависящую от n+ 2 переменных, легко реализовать на двух стробируемых мультиплексорах и двух инверторах. Один из инверторов используется в цепи стробирования одного из мультиплексоров, а другой на их информационных входах.
Рассмотрим пример. Пусть требуется реализовать ПФ y, представленную картой Вейча на рис. 1.16, на стробируемых мультиплексорах MS 4 1, имеющих три состояния выхода и активный уровень 0 на их стробирующих входах. Представим карту Вейча на рис. 1.16 в виде двух карт Вейча, зависящих от трех младших переменных (см. рис. 1.17).
1, имеющих три состояния выхода и активный уровень 0 на их стробирующих входах. Представим карту Вейча на рис. 1.16 в виде двух карт Вейча, зависящих от трех младших переменных (см. рис. 1.17).
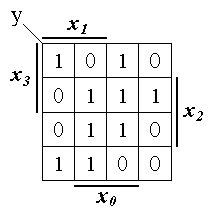
Рис. 1.16. Задание ПФ y.
Подавая переменную х3 непосредственно на стробирующий вход одного из мультиплексоров MS 4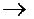 1, мы реализуем функцию y1, представленную картой Карно, показанной на рис. 1.17, и через дополнительный внешний инвертор на вход другого, мы реализуем функцию y2, представленную картой Карно, показанной на рис. 1.17.
1, мы реализуем функцию y1, представленную картой Карно, показанной на рис. 1.17, и через дополнительный внешний инвертор на вход другого, мы реализуем функцию y2, представленную картой Карно, показанной на рис. 1.17.
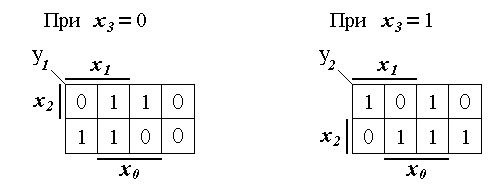
Рис. 1.17. Представление карты Вейча (рис. 1.16)
Очевидно, что y= y1 + y2, причем логическая операция ИЛИ реализуется здесь как монтажная операция соединением в единую цепь выходов этих двух мультиплексоров. Подавая переменные х2 и х1 на соответствующие адресные входы a1 и a0, а переменную х0 непосредственно или через второй дополнительный внешний инвертор вместе с константами 0 и 1 на информационные входы мультиплексоров, получаем окончательную реализацию ПФ (см. рис.1.18).
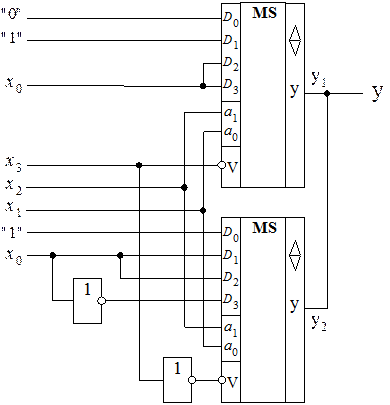
Рис. 1.18. Реализация ПФ y на двух мультиплексорах
Функции y1 и y2 можно реализовать по рациональным структурам, способы получения которых описаны выше.
УСТАНОВКА УМ 11М. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ
В основе принципа работы установки лежит метод изучения функциональных и электрических характеристик логических элементов и устройств цифровой техники (дешифраторов, мультиплексоров, счетчиков и т.д.) путем подачи входных воздействий и наблюдения и анализа выходных реакций элемента на эти воздействия.
Источником входных воздействий, кроме сигналов, вырабатываемых блоком задающим, могут служить логические уровни с выходов переключательных регистров блоков логических, а также сигналы, сформированные с помощью других логических элементов. Входные воздействия подключаются на входе исследуемого элемента с помощью коммутационных шнуров.
Реакцию изучаемого элемента можно изучать с помощью осциллографа или индикаторов единичных, подключаемых на выход самого элемента.
Конструктивно установка состоит из следующих узлов:
• корпуса;
•рамы;
• функциональных блоков:
1) блока задающего;
2) блока логического 1;
3) блока логического 2;
4) блока дешифраторов;
5) блока мультиплексоров;
6) блока установочного;
7) блока счетчиков;
• платы ИИ, выполняющей функцию блока питания установки.
На панели выведены контрольные и коммутационные гнезда, а также индикаторы единичные, установленные и распаянные в печатных платах.
У сменных блоков (блока дешифраторов, блока мультиплексоров, блока установочного и блока счетчиков) платы снизу закрываются дном из прозрачного оргстекла.
Функциональные блоки имеют четыре типоразмера. Каждый из блоков может быть установлен только на свое определенное место на раме.
На лицевых панелях функциональных блоков нанесены мнемонические схемы элементов и устройств, входящих в блок.
Блок задающий служит для задания входных воздействий на изучаемые элементы.
Блок логический 1
Переключательный регистр блока вырабатывает на своих гнездах потенциальные уровни логического 0 и логической 1.
Когда кнопка не нажата, на верхнем гнезде пары уровень логической единицы, на нижнем - уровень логического нуля.
Если кнопка нажата, на верхнем гнезде пары уровень логического нуля, на нижнем - уровень логической единицы.
Логические элементы И (микросхема К155ЛИ1, обозначенные на панели "&") выполняют функцию "конъюкции" входных переменных.
Логические элементы "отрицание равнозначности" (микросхема К155ЛП5, обозначенные на панели "=1") выполняют функцию "сумма по модулю 2" входных переменных.
Логические элементы ИЛИ (микросхема К155ЛЛ1, обозначенные на панели "1") выполняют функцию "дизъюнкции" входных переменных.
Логические элементы "повторитель" с тремя состояниями выхода (микросхема К155ЛП8, обозначенные на панели "1", обозначение входов "X" и "EZ") осуществляют передачу сигналов со входа "X" на выход при наличии уровня логического нуля на управляющем входе "EZ". При наличии на входе "EZ " уровня логической единицы выход элемента переходит в высокоимпедансное состояние.
Триггерные схемы с комбинированными входами, с динамическим управлением записью типа D) (микросхемы К155ТМ2) имеют непосредственную индикацию на прямом выходе.
Индикаторы единичные блока «загораются» при подаче на входы уровня логической единицы и гаснут при подаче уровня логического нуля.
При незадействованных входах индикаторы «гореть» не должны.
Блок логический 2
Логические элементы И-ИЛИ-НЕ (микросхема К155ЛР1, обозначенные на панели &1) выполняют функцию Х1ΛХ2 v ХЗΛХ4, где Λ- конъюнкции, v- дизъюнкция, Х1, Х2, ХЗ, Х4 - входные переменные.
Логические элементы "расширитель" (микросхема К155ЛД1, обозначенные на панели & , обозначение выходов "К" и "Е") при подключении к расширяемому элементу И-ИЛИ-НЕ выполняют функцию И - конъюнкции входных переменных, а расширяемый элемент - функцию ИЛИ-НЕ. Соединяемые выводы расширителя и расширяемого элемента обозначены буквами "К" и "Е".
Логические элементы И-НЕ (микросхемы К155ЛАЗ, К155ЛА1, К155ЛА4, обозначенные на панели "&" со знаком инверсии на выходе) выполняют функцию "отрицание конъюнкции" входных переменных.
Логические элементы ИЛИ-НЕ (микросхема К155ЛЕ4, обозначенные на панели "1" со знаком инверсии на выходе) выполняют функцию "отрицание дизъюнкции" входных переменных.
Триггерные схемы с комбинированными входами со статическим управлением записью (микросхемы К155ТВ1) являются триггерами J—К типа и имеют встроенную индикацию состояния на прямом выходе.
К гнездам, обозначенным "+", подключено напряжение +5 В через резистор 1 кОм. К гнездам, обозначенным " ┴", подключен вывод "общий" источника питания.
Блок мультиплексоров
Сдвоенный мультиплексор 4-1 (микросхема К155КП2) позволяет решать следующие функции:
• выбор одного из информационных каналов;
• реализация логической функции параллельно-последовательного преобразователя;
• мультиплексирование с 4 линий на 1.
Сигнал на выходе мультиплексора с канала, определяемого адресными входами "1" и "2" появляется только при наличии на входе ERD уровня логического нуля (см. табл. 2.1).
Таблица 2.1 - Таблица истинности состояний сдвоенного мультиплексора К155КП2
| Адресные входы | Входы верхние | Выход | ( Входы нижние | Выход | |||||||||
| ERD1 | ERD2 | ||||||||||||
| Х | X | X | X | X | X | X | X | X | X | ||||
| X | X | X | X | X | X | ||||||||
| X | X | X | X | X | X | ||||||||
| X | X | X | X | X | X | ||||||||
| X | X | X | X | X | X | ||||||||
| X | X | X | X | X | X | ||||||||
| X | X | X | X | X | X | ||||||||
| X | X | X | X | X | X | ||||||||
| X | X | X | X | X | X |
X - значение сигнала на входе любое - "0" или "1", не влияет на состояние выходов.
Мультиплексор на 8 каналов (микросхема К155КП7) осуществляет передачу информации с одного из входов "0, 1...7", выбранного по коду адреса на адресных входах "I", "2", "4" при наличии потенциала низкого уровня на входе стробирования ERD. Таблица истинности состоянии приведена в табл.2.2.
Таблица 2.2. - Таблица истинности состояний мультиплексора К155КП7
| Состояние входов | Состояние выходов | ||||||||||||
| информационных DO 1 2 3 4 5 6 7 | ERD | адресных 0 1 2 | прямого | инверсного | |||||||||
| X | X | X | X | X | X | X | X | X | X | X | 0 | ||
| X | X | X | X | X | X | X | 0 | ||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | I | X | ||||||
| X | X | X | X | X | X | X | |||||||
| X | X | X | X | X | X | X |
X - значение сигнала на входе любое - "0" или "1" - не влияет на состояние вводов.
Четырехразрядный мультиплексор 2-1 (микросхема КР531КП11) осуществляет передачу информации с одного из двух входов, выбранных с помощью адресного сигнала "А" на вход существующего разряда при наличии на стробирующем входе "EZ" сигнала низкого уровня. При подаче на вход "EZ" сигнала высокого уровня все выходы ZO, Z1, Z2, Z3 мультиплексора устанавливаются в состояние высокого импеданса. Таблица истинности состояний приведена в табл. 2.3.
Таблица 2.3 - Таблица истинности состояний мультиплексора КР531КП11
| Состояние входов | Состояние выходов | ||||||||||||
| информационных 0 1 2 3 4 5 6 7 | EZ | адрес SE | ZO | Z1 | Z2 | Z3 | |||||||
| X | Х | X | X | X | X | X | X | X | Z | Z | Z | Z | |
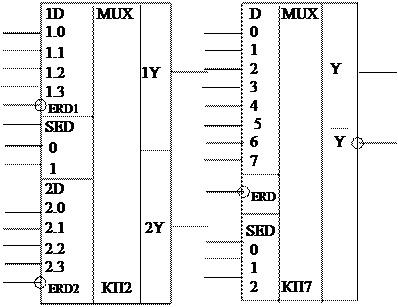 |  | ||
Рис. 2.1. Условные графические обозначения мультиплексоров
3. Задание на лабораторную работу
1. Ознакомиться с теоретической частью.
2. Изучить описание лабораторного стенда УМ-11 или УМ-11М.
3. Выполнить синтез оптимальных схем на основе мультиплексоров и собрать их на стенде. При отсутствии мультиплексора на нужное число входов синтезировать мультиплексор по линейной или пирамидальной структуре.
4. Продемонстрировать работу схем преподавателю.
5. Оформить отчет по лабораторной работе.
Таблица индивидуальных заданий
для синтеза одновыходовой комбинационной схемы на мультиплексорах
Таблица 3.1.
| № вари-анта | Реализуемая переключательная функция | № вари-анта | Реализуемая переключательная функция |
| f 4 = Ù (0, 5, 6, 7, 9, 10, 13, 14) | f 4 = Ú (3, 6, 8, 11, 15), ÙÚ (0) | ||
| f 4 = Ú (2, 4, 13, 15), ÙÚ (7, 12) | f 4 = (0, 3, 4, 5, 9), ÙÚ (10, 11, 12) | ||
| f 4 = Ú (0, 4, 9, 10, 11, 13, 15) | f 4 = Ú (0, 1, 7, 9, 10, 13), ÙÚ (4) | ||
| f 4 = Ú (3, 4, 7, 10, 11), ÙÚ (1, 13) | f 4 = Ú (1, 5, 7, 10, 11,), ÙÚ (3) | ||
| f 4 = Ú (0, 1, 2, 4, 7, 8, 13), ÙÚ (6) | f 4 = Ú (1, 3, 4, 7, 9, 15), ÙÚ (0) |
Таблица индивидуальных заданий
для синтеза одновыходовой комбинационной схемы на мультиплексорах
Таблица 3.2.
| № варианта | Реализуемая переключательная функция | № вари-анта | Реализуемая переключательная функция |
| f 5 = Ú (0, 4, 20, 21) | f 5 = Ú (6, 9, 10, 17, 19 ) | ||
| f 5 = Ú ( 7, 9, 22, 23) | f 5 = Ú (8, 9, 10, 11, 21) | ||
| f 5 = Ú (2, 10, 15, 19) | f 5 = Ú (0, 1, 3, 20, 22) | ||
| f 5 = Ú ( 1, 3, 5, 11, 17) | f 5 = Ú (3, 4, 8, 10, 20) | ||
| f 5 = Ú (4, 11, 12, 16, 18) | f 5 = Ú (0, 4, 10, 13, 20) |
Примечание. Мультиплексор на 4 входа реализуется с использованием линейной структуры (см. Приложение Б).
Приложение А
Пример реализации ПФ на мультиплексоре
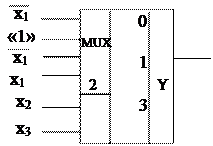
При помощи мультиплексора можно легко синтезировать ПФ n аргументов, подавая соответствующие значения на каждый из m информационных входов. Схема для реализации ПФ f2 = Ú (0, 2) приведена на рисунке А.1.
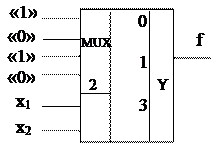 | |||
|
ПФ n аргументов можно реализовать, используя мультиплексор с (n–1) селектирующими входами. Для этого строится таблица значений ПФ, значения ПФ разбиваются на группы, в которых старшие аргументы сохраняют свои значения. В пределах группы ПФ может принимать значения «1», «0», либо прямое или инверсное значение младшего аргумента. Рассмотрим пример.
Построим таблицу значений для ПФ f3 = Ú (0, 2, 3, 4, 7) (табл. А.1), где группы выделены жирными линиями. Видно, что в нулевой и второй группе f3 = 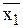 , в первой группе f3 = «1», в третьей группе f3 =
, в первой группе f3 = «1», в третьей группе f3 = 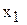 , поэтому можно использовать мультиплексор не с тремя, а двумя селектирующими входами (рисунок А.2).
, поэтому можно использовать мультиплексор не с тремя, а двумя селектирующими входами (рисунок А.2).
Поясним работу схемы. Пусть значения аргументов принадлежат группе 0 табл. А.1, тогда к выходу f будет подключен информационный вход 0 мультиплексора, и на выходе будет присутствовать инверсное значение аргумента x1.
| Таблица А.1 Значения ПФ f3 = Ú (0, 2, 3, 4, 7) | ||||||||
| Аргументы и функция | Значения на наборах 0 – 7 /группы | |||||||
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| f | ||||||||
| f ( x1) |
 | |||
|
Приложение Б
Пример расширения разрядности мультиплексора
При использовании линейной структуры младшие разряды управляющего кода подаются на соединенные вместе входы мультиплексоров 1-й ступени, выходы которых соединяются со входами элемента ИЛИ, выход которого является выходом схемы. Старшие разряды управляющего кода подаются на дешифратор, который разрешает работу одного из мультиплексоров 1-й ступени.
Пример. Синтезировать схему мультиплексора 16:1 на ИМС КР1533КП7 (линейная и пирамидальная структура)
Решение. Для реализации функции 16:1 нужно иметь 4 управляющих входа, т.к. log216 = 4. ИМС КР1533КП7 реализует функцию 8:1, т.е. необходимо иметь 2 таких мультиплексора.
Линейная структура приведена на рисунке Б.1. Для управления двумя мультиплексорами достаточно 1 разряда двоичного кода, поэтому в данном примере можно обойтись и без дешифратора (использовать обычный инвертор), дешифратор использован для иллюстрации способа его подключения. Дешифратор DD1 разрешает работу мультиплексора DD2 входных данных y1 ¸ y8 при x4 = 0, при x4 = 1 дешифратор DD1 разрешает работу мультиплексора DD3 входных данных y9 ¸ y16 . Значения на управляющих входах DD2 и DD3 определяют, с какого входа входные данные поступают на выход мультиплексора. Так как мультиплексор имеет и инверсный выход, то в качестве элемента, выполняющего функцию 2ИЛИ, можно выбрать элемент Шеффера 2И-НЕ, подавая аргументы на его входы в инверсном виде.
 |
Рисунок Б.1 – Мультиплексор 16:1 на ИМС КР1533КП7 (линейная структура)
