Частные случай расчета надежности
1. Объект (далее ОБ) состоит из n блоков, соединенных последовательно (см. рис. 3). Вероятность безотказной работы каждого блока p. Найти вероятность безотказной работы P системы в целом.

Решение: P=pn
2. ОБ состоит из n блоков, соединенных параллельно (см. рис. 4). Вероятность безотказной работы каждого блока p. Найти вероятность безотказной работы P системы в целом.
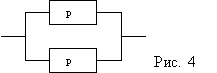
Решение: P=1-(1-p)2
3. ОБ состоит из n блоков, соединенных параллельно (см. рис. 5). Вероятность безотказной работы каждого блока p. Вероятность безотказной работы переключателя (П) p1. Найти вероятность безотказной работы P системы в целом.
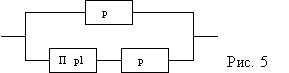
Решение: P=1-(1-p)*(1-p1*p)
4. ОБ состоит из n блоков (см. рис. 6), с вероятность безотказной работы каждого блока p. С целью повышения надежности ОБ произведено дублирование, еще такими-же блоками. Найти вероятность безотказной работы системы: с дублированием каждого блока Pa, с дублированием всей системы Pb.
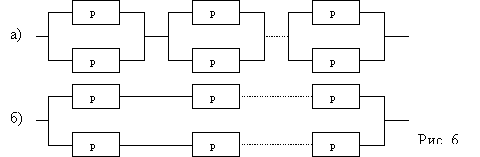
Решение: Pa=[1-(1-p)2]n Pb=[1-(1-p)n]2
5. ОБ состоит из n блоков (см. рис. 7), с вероятность безотказной работы каждого блока p, величина которой условно показаны на рисунке. С целью повышения надежности ОБ произведено дублирование, еще такими-же блоками, наименее надежных блоков. Найти вероятность безотказной работы P системы.

Решение: P=[1-(1-p1)2]*[1-(1-p2)3]*p3*p4*[1-(1-p5)*(1-p6)]
6. ОБ состоит из 3-х узлов (см. рис. 8). В первом узле n1 элементов, во втором узле n2 элементов. В третьем узле n3 элементов. Вероятность безотказной работы каждого элемента p. Найти вероятность безотказной работы P системы.
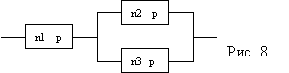
Решение: P1=pn1 P2=pn2 P3=pn3
P23=1-(1-pn2)*(1-pn3)
P= pn1*[1-(1-pn2)*(1-pn3)]
7. ОБ состоит из 2-х узлов U1 и U2, соединенных последовательно, и стабилизатора C (см. рис. 9). При исправном C вероятность безотказной работы U1=p1, U2=p2. При неисправном C вероятность безотказной работы U1=p1', U2=p2'. Вероятность безотказной работы C=ps. Найти вероятность безотказной работы P системы в целом.
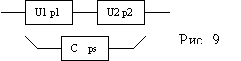
Решение: P=ps*p1*p2+(1-ps)*p’1*p’2
8. ОБ состоит из 2-х узлов U1 и U2, соединенных параллельно, и стабилизатора C (см. рис. 10). При исправном C вероятность безотказной работы U1=p1, U2=p2. При неисправном C вероятность безотказной работы U1=p1', U2=p2'. Вероятность безотказной работы C=ps. Найти вероятность безотказной работы P системы в целом.
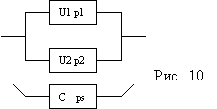
Решение: P=ps*[1-(1-p1)*(1-p2)]+(1-ps)*[1-(1-p1')*(1-p2')]
9. ОБ состоит из 2-х узлов U1 и U2. Вероятность безотказной работы за время t узлов: U1 p1=0.8, U2 p2=0.9. По истечении времени t ОБ несправен. Найти вероятность, что:
- H1 - неисправен узел U1
- H2 - неисправен узел U2
- H3 - неисправны узлы U1 и U2
Решение: Очевидно, имело место H0, когда оба узла исправны.
Событие A=H1+H2+H3
Априорные (первоначальные) вероятности:
- P(H1)=(1-p1)*p2=(1-0.8)*0.9=0.2*0.9=0.18
- P(H2)=(1-p2)*p1=(1-0.9)*0.8=0.1*0.8=0.08
- P(H3)=(1-p1)*(1-p2)=(1-0.8)*0.9=0.2*0.1=0.02
- A=i=13*P(Hi)=P(H1)+P(H2)+P(H3)=0.18+0.08+0.02=0.28
Апостерионые (конечные) вероятности:
- P(H1/A)=P(H1)/A=0.18/0.28=0.643
- P(H2/A)=P(H2)/A=0.08/0.28=0.286
- P(H3/A)=P(H3)/A=0.02/0.28=0.071
10. ОБ состоит из m блоков типа U1 и n блоков типа U2. Вероятность безотказной работы за время t каждого блока U1=p1, каждого блока U2=p2. Для работы ОБ достаточно, чтобы в течение t работали безотказно любые 2-а блока типа U1 и одновременно с этим любые 2-а блока типа U2. Найти вероятность безотказной работы ОБ.
Решение: Событие A (безотказная работа ОБ) есть произведение 2-х событий:
- A1 - (не менее 2-х из m блоков типа U1 работают)
- A2 - (не менее 2-х из n блоков типа U2 работают)
Число X1 работающих безотказно блоков типа U1 есть случайная величина, распределенная по биномиальному закону с параметрами m, p1. Событие A1 состоит в том, что X1 примет значение не менее 2, поэтому:
P(A1)=P{X1>2}=1-P(X1<2)=1-P(X1=0)-P(X1=1)=1-(g1m+m*g2m-1*p1), где g1=1-p1
аналогично: P(A2)=1-(g2n+n*g2n-1*p2), где g2=1-p2
Вероятность безотказной работы ОБ:
R=P(A)=P(A1)*P(A2)=[1-(g1m+m*g2m-1*p1)]*[1-(g2n+n*g2n-1*p2)], где g1=1-p1, g2=1-p2
11. ОБ состоит из 3-х узлов (см. рис. 11). В узле U1 n1 элементов с интенсивностью отказов l1. В узле U2 n2 элементов с интенсивностью отказов l2. В узле U3 n3 элементов с интенсивностью отказов l2, т.к. U2 и U3 дублируют друг друга. U1 выходит из строя если в нем отказало не менее 2-х элементов. U2 или U3, т.к. дублируются, выходят из строя если в них отказал хотя бы один элемент. ОБ выходит из строя если отказал U1 или U2 и U3 вместе. Вероятность безотказной работы каждого элемента p. Найти вероятность того, что за время t ОБ не выйдет из строя.
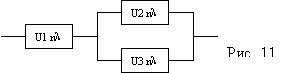
Решение: Вероятность выхода из строя одного элемента U1, U2 или U3 за t равны:
p1=1-e-1*t p2=p3=1-e-2*t
Вероятность выхода из строя U1 за t равна:
R1=1-(1-p1)n1*n1*p1*(1-p1)n1-1
Вероятности выхода из строя U2 и U3 равны:
R2=1-(1-p2)n2 R3=1-(1-p3)n3
Вероятности выхода из строя всего ОБ:
R=R1+(1-R1)*R2*R3
Литература:
Малинский В.Д. и др. Испытания радиоаппаратуры, "Энергия", 1965 г.
ГОСТ 16503-70 - "Промышленные изделия. Номенклатура и характеристика основных показателей надежности".
Широков А.М. Надежность радиоэлектронных устройств, М, Высшая школа, 1972 г.
ГОСТ 18322-73 - "Системы технического обслуживания и ремонта техники. Термины и определения".
ГОСТ 13377-75 - "Надежность в технике. Термины и определения".
Козлов Б.А., Ушаков И.А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики, М, Сов. Радио, 1975 г.
Перроте А.И., Сторчак М.А. Вопросы надежности РЭА, М, Сов. Радио, 1976 г.
Левин Б.Р. Теория надежности радиотехнических систем, М, Сов. Радио, 1978 г.
ГОСТ 16593-79 - "Электроприводы. Термины и определения".
И. Брагин 08.2003 г.
7.4. Методы повышения надежности [1, 2]
