Нормальный закон распределения погрешностей

Для характеристики свойств случайной величины в теории вероятности используется понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии используют преим. Дифференциальную – закон распределения плотности вероятностей случайной величины.

Пусть произведено n=50 наблюдений величины x_i : x₁, x₂ x₃,….x_n,

Номер интервала
nk
nk/n	0,1	0,2	0,36	0,22	0,12

Найдем размах ряда L = x_max, - x_{min = 29-19=10} Разделив размах ряда на k=5 равных интервалов Dl = L/k = 10/5=2, подсчитаем количество наблюдений n_k , попадающих в каждый интервал.

При бесконечном повторении и увеличении n ступенчатая кривая перейдет в плавную кривую f(x) – кривая плотности распределения вероятности случайной величины.(Или r)

Числовые характеристики распределений:

1. Математическое ожидание (среднее арифметическое):

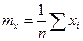= 25

2. Среднее квадратичное отклонение (СКО) или рассеивание единичных результатов и дисперсияч:

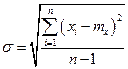D = s²,

где D – дисперсия.

Качество и точность измерений тем выше, чем меньше СКО, тем меньше вероятность рассеивания результатов наблюдений D.

Рис 1.12. Графики нормального закона распределения плотности вероятности случайных погрешностей

Чаще начало координат совмещают с центром распрелделения.

В аналитической форме закон нормального закона распределения записывают:

f(x)= .

где s – среднеквадратическое отклонение(СКО), характеризующее точность выполненных измерений (чем меньше s, тем выше точность). По мере уменьшения s рассеяние случайных погрешностей D относительно центра их распределения, (в данном случае относительно значения D= 0) уменьшается. На рис. 1.12 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратичного отклонения. Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.

На графике плотности вероятности для конкретного СКО (см. рис. 1.12) вероятность численно равна площади S заштрихованной фигуры, ограниченной функцией r(D), отрезком оси D от –D_Г1 до D_Г1 и ординатами r(–D_Г1), r(D_Г1). Чем шире заданный интервал погрешностей, тем больше площадь S, т.е. больше вероятность попадания случайных погрешностей измерений D в этот интервал. Для интервала (–¥,+¥) вероятность R(–¥ £ D £ +¥) =1.

Более универсальным методом является оценки погрешности с использованием доверительных интервалов: На графике норм. распределения отложены интервалы с границами ±s ±2s и т.д.

Доверительные вероятности для этих интервалов в таб. В технике принят 99% уровень надежности, т.е. границы ±3s.