Гидрология и регулирование стока
Лекция 1- Предмет гидрологии
Гидрология - это наука, изучающая гидросферу, ее свойства и протекающие в ней процессы и явления во взаимодействии с атмосферой, литосферой и биосферой.
Гидрология делится на океанологию (гидрологию морей и океанов) и гидрологию вод суши.
Основным предметом изучения нашего курса является гидрология вод суши. Гидрология вод суши включает в себя:
1. гидрографию, дающую общее описание водных объектов (географическое положение, размеры, режим, местные условия);
2. гидрометрию, изучающую методы определения и измерения характеристик водных объектов;
3. общую гидрологию, изучающую физическую сущность и закономерности гидрологических явлений;
4. инженерную гидрологию, разрабатывающую методы гидрологических прогнозов и расчетов.
Гидрология связана с такими науками как гидравлика, гидрофизика, теория вероятности и математическая статистика, метеорология и другие.
Роль гидрологии в водохозяйственном строительстве
Решение всех водохозяйственных проблем начинается с гидрологических исследований и гидрологических расчетов. На гидрологических данных базируется как использование водных объектов, так и осуществление водохозяйственного строительства.
К наиболее важным вопросам, которые решает гидрология относятся:
1. оценка водных запасов и водного баланса объекта;
2. установление расчетных расходов воды и внутригодового распределения стока;
3. расчет объемов воды испаряющихся с поверхности водохранилищ и речных бассейнов;
4. исследования формирования русел рек и берегов водохранилищ;
5. характеристика температурного и ледового режима рек и озер;
6. прогнозы основных элементов гидрологического режима;
7. исследование возможностей преобразования природных условий путем перераспределения водных ресурсов во времени и между различными регионами.
Водные объекты с древних времен играют важную роль в жизни народов.
Первые гидрометрические измерения были проведены в Египте за уровнем воды в реке Нил около 4 тысяч лет назад.
В России инженерные наблюдения рек, озер и водоемов начались со времен Петра I. Тогда же было осуществлено и первое крупное водохозяйственное строительство. Создана система, соединяющая Волгу с Балтикой, построены Ладожские каналы. В 1715г. На реке Неве у Петропавловской крепости был оборудован первый водомерный пост. В это же время было начато строительство Волго-Донского канала и многое другое.
Планомерное изучение водных объектов России началось с 1874 года, когда при Министерстве путей сообщения была создана специальная навигационно-описная комиссия. Под ее началом было организовано около 500 водомерных постов и гидрометрических створов. В конце 19в. большое развитие получили и научные работы, связанные с изучением гидравлических режимов рек, движением наносов и формированием речного русла под руководством крупного инженера – гидролога В.М. Лохтина, являющегося основоположником гидрологии речного русла. Бурное развитие гидрология переживала в советский период. В это время в нашей стране был построен целый каскад гидроэлектростанций (ГЭС), в том числе крупнейшая в нашей стране Саяно-Шушенская ГЭС.
На территории России протекает около 2 млн. рек. По объему годового стока самые крупные реки в нашей стране это: Енисей (548 км 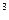 воды), Лена (488 км
воды), Лена (488 км 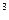 ), Обь (394 км
), Обь (394 км 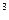 ), Амур (346 км
), Амур (346 км 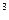 ), Волга (256 км
), Волга (256 км 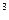 ).
).
Круговорот воды в природе. Мировой водный баланс.
Под действием солнечных лучей с поверхности океана происходит испарение воды. В результате испарения образуются облака, которые относятся ветром. Из облаков, не достигших берега, выпадает дождь на поверхность океана. Так происходит малый круговорот воды в природе.
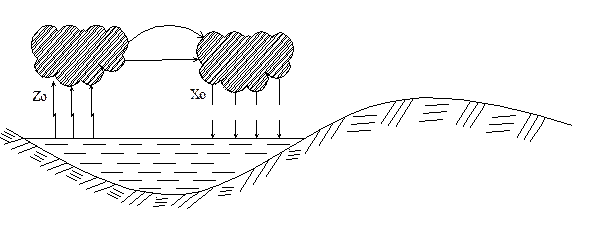 Рисунок 1 - Схема малого круговорота воды
Рисунок 1 - Схема малого круговорота воды
При большом круговороте воды в природе часть испарившейся с океана воды выпадает в виде дождей и на поверхность суши. При этом выпавшие осадки попадают в реки, образуя поверхностный сток; просачиваются в толщу грунта, пополняя грунтовый сток, гидравлически связанный с речным стоком. В конечном счете, вся выпавшая в виде осадков вода реками вновь возвращается в океан, завершая большой круговорот воды в природе.
 Рисунок 2 - Схема большого круговорота воды
Рисунок 2 - Схема большого круговорота воды
На приведенных схемах:
Z – слой испарения, представляющий собой отношение полного объема испарившейся воды к площади земного шара.

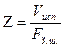 , (мм),
, (мм),
где индекс «О» - относится к океану,
индекс «С» - относится к суши.
X, Y – обозначают, соответственно, слои осадков и стока, которые рассчитываются также через отношение объемов к площади земного шара.
Уравнение водного баланса для океана:
Zo=Xo+Y
для суши:
Xc=Zc+Y
Решая совместно эти уравнения можно получить уравнение мирового водного баланса:
Zo+Zc=Xo+Xc.
Река и ее система.
Река – водный поток в естественном русле.
Река, не впадающая в другие реки, называется главной.
Река, впадающая в главную, называется притоком первого порядка. Река, впадающая в приток первого порядка, называется притоком второго порядка, и т.д.
Все реки и ручьи, связанные с одной главной рекой, составляют речную систему.
Гидрографическая сеть – это все реки, озера, водоемы, пруды, болота на данной территории.
Длина реки – длина линии с учетом масштаба, проведенная на карте вдоль и посередине реки.
Густота речной сети ( 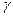 ) – представляет собой отношение суммы длин всех рек данной системы к площади, занимаемой этой системы.
) – представляет собой отношение суммы длин всех рек данной системы к площади, занимаемой этой системы.
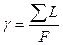 , (
, ( 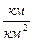 )
)
В тех районах, где больше выпадает осадков, больше и густота речной сети.
Извилистость (характеризуется Кизв. (коэффициентом извилистости)) – это отношение длины реки L к длине спрямляющей линии Lc, соединяющей исток и устье реки.
Кизв.= 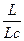 всегда > 1,
всегда > 1,
причем у малых рек извилистость больше ( у Волги Кизв.=2,24).
Продольный и поперечный профили реки. 
Продольный профиль – изменение отметки водной поверхности или отметки дна для горной реки по длине.
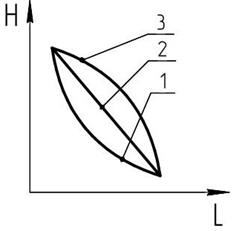
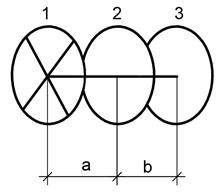
Рисунок 3 – Характерные профили рек.
1 - равнинные реки;
2 - реки предгорий;
3 – горные реки.
На рисунке изображены наиболее характерные профили рек, приуроченных к различным типам рельефа.
Для равнинных рек наклон линии водной поверхности больше в верхнем течении. Отношение перепада высот уровней водной поверхности ( 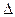 Н) к длине (L), на которой произошел этот перепад, называется уклоном (I):
Н) к длине (L), на которой произошел этот перепад, называется уклоном (I):
I= 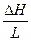 ∙103, (%о – промилле)
∙103, (%о – промилле)
Промилле представляет собой тысячную долю единицы.
Волга в верхнем течении имеет уклон 0,17%о, в среднем течении уклон равен 0,06%о, в нижнем – 0,02%о.
Уклон – это величина, которая определяет скорость течения воды в реке и расход воды в реке. В связи с этим, практически значимой является задача определения среднего уклона по длине реки. Решается данная задача графическим способом:
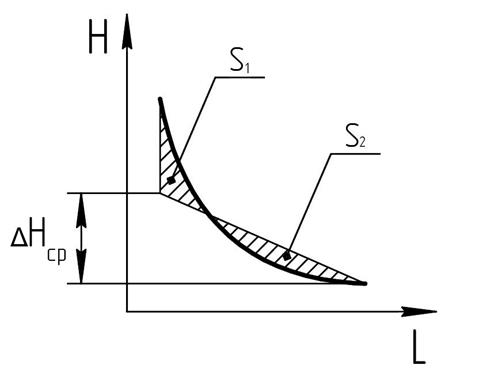
Рисунок 4 – Схема определения среднего уклона реки.
Из окончания профиля надо провести секущую линию таким образом, чтобы площади, образующиеся под профилем S1 и над ним S2, были равны между собой. Тогда
Iср = 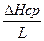
Поперечный профиль – это изменение водной поверхности по ширине реки. Он формируется под действием трех причин:
1. действие ветра:
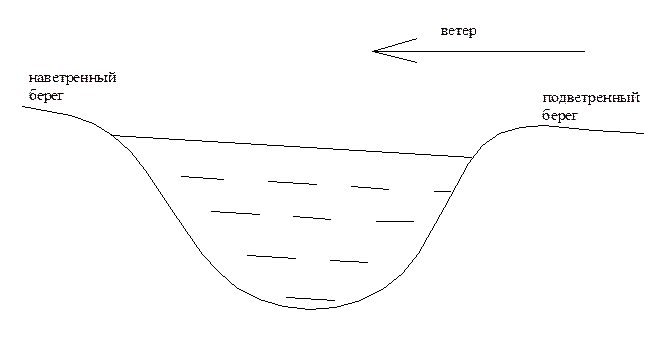 2. действие центробежной силы на поворотах реки:
2. действие центробежной силы на поворотах реки:
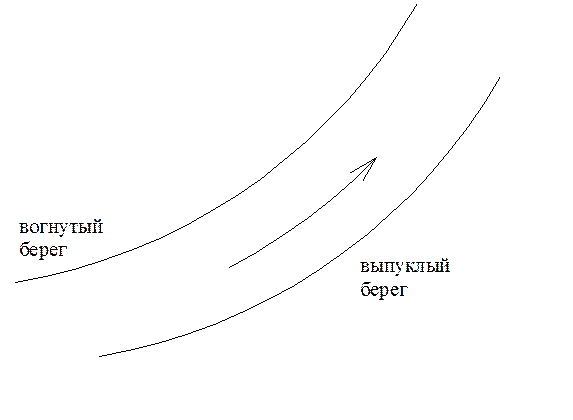
Рисунок 5
Под действием центробежной силы наблюдается повышение уровня воды в реке у выпуклого берега.
3. действие Кориолисовой силы, обусловленное вращением Земли.
Вследствие вращения Земли у всех рек северного полушария, текущих с севера на юг, уровень воды всегда выше у правого берега, и наоборот.
Лекция 2: Речной бассейн. Долина и русло реки.
Речной бассейн – площадь земной поверхности, с которой вода поверхностным стоком собирается в данную реку. Границей бассейна являются водоразделы, которые проходят по более высоким отметкам земной поверхности.
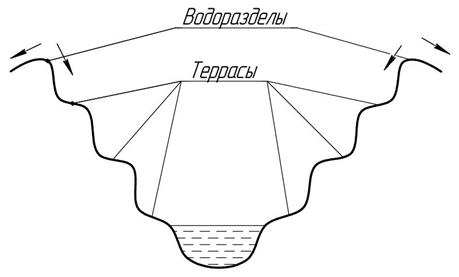
Рисунок 6 -
Морфометрические характеристики бассейна:
1. Площадь бассейна (Fб, км  );
);
2. Длина бассейна (Lб, км.).
На карте примерно вдоль реки проводятся две прямые, одна из его устья, а вторая из истока. И наиболее протяженная из них принимается в качестве длины бассейна.
3. Ширина бассейна:
(Вб = 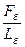 , км.)
, км.)
4. Средний уклон бассейна:
Iср = 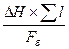 ∙103, (%о),
∙103, (%о),
где 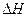 - перепад высот между соседними горизонталями;
- перепад высот между соседними горизонталями;
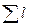 - сумма длин горизонталей на карте с учетом масштаба.
- сумма длин горизонталей на карте с учетом масштаба.
Морфометрические характеристики бассейна определяют характеристики и самой реки:
Долина реки – продольная, пониженная, с уклоном в одну сторону форма рельефа, по дну которой течет река.
Русло – часть долины, занятая рекой. Склон долины редко бывает ровным и на нем образуются более или менее горизонтальные площадки, которые называются террасами.
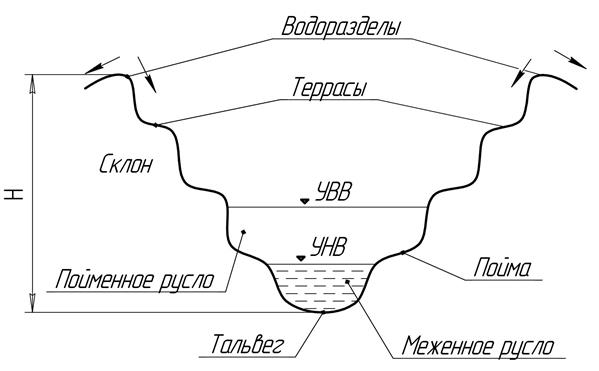
Рисунок 7
Пойма – терраса, заливаемая при уровне высоких вод (УВВ).
Тальвег – линия, проходящая через самые низкие точки речной долины. Глубина долины (Н) для равнинных рек может достигать 300м, а для горных рек несколько км.
Характеристики русла:
1. Ширина В, м.
2. Водное сечение – сечение русла поверхностью, перпендикулярной в каждой своей точке линиям водотока.
Та часть водного течения, где наблюдается движение воды, называется «живым» cечением. Часть, где течение отсутствует, называется «мертвым» cечением.
3. Средняя глубина – отношение площади водного сечения к ширине русла:
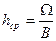 .
.
4. Гидравлический радиус:
R= 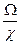 ,
,
где 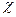 - смоченный параметр.
- смоченный параметр.
5. Критерий Рейнольдса:
Re= 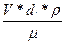 , (ведро молока! )
, (ведро молока! )
где V- средняя скорость движения потока;
dэ- эквивалентный диаметр;
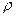 - плотность воды;
- плотность воды;
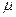 - коэффициент динамической вязкости.
- коэффициент динамической вязкости.
Для проведения гидравлических расчетов данная формула может быть несколько изменена:
Re= 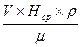 .
.
Число Рейнольдса характеризует режим движения воды в реке.
Когда Re<300 наблюдается ламинарное или параллельно-струйное движение воды в реке. При Re>300 имеет место турбулентное или вихревое движение, характеризующееся интенсивным перемешиванием жидкости, при сохранении общего поступательного движения.
Для характеристики реки в плане используют ряд дополнительных понятий:
1. Стрежень – линия на поверхности воды, проходящая через точки с самой высокой поверхностной скоростью.
2. Динамическая ось потока – линия, проходящая через точки с самыми высокими скоростями:
3. Исток – место, где водный поток приобретает отчетливое очертание.
4. Устье – место, где река впадает в океан, море, озеро, болото или в другую реку или где река пропадает («слепое» устье).
Если устье состоит из одного рукава, то называется эстуарий. Если из многих рукавов, то дельтой.
5. Рукав – часть устья отделенная от основного устья островом.
6. Плес – глубокое спокойное место на реке.
7. Перекат – неглубокое место с большим течением.
8. Отмель – место в русле реки с небольшой глубиной, обсыхающее при низком уровне.
9. Пляж – часть склона, образованная речными наносами .
10. Залив – часть русла, глубоко впадающая в берег.
Основные расчетные гидрологические характеристики.
В соответствии со СНиП определяют:
1. Расход воды в реке Q, м 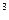 /с;
/с;
2. Объем стока V=Q×365×86400×10 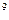 , км
, км 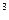 ,
,
Где 365 – количество дней в году; а 86400 - количество секунд в сутках;
3. Модуль стока М= 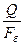 , м
, м 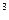 /с×км
/с×км 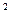 ;
;
4. Слой стока у= 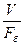 , мм;
, мм;
5. Уровень Н, см.
Лекция 3: Уровенный режим. Частота и вероятность. Продолжительность и обеспеченность.
Уровень – расстояние по вертикали от произвольно выбранного, но постоянного начала (нуля графика), до поверхности воды.
Нуль графика выбирается таким образом, чтобы отметки от него всегда были положительными, при этом дно реки не может являться таковым, так как оно постоянно либо размывается, либо заиляется.
Уровенный режим – изменение уровня во времени вследствии изменения питания реки, деформации русла или изменения условий регулирования.
Уровень зависит от ряда факторов:
1. климатических (t 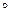 воздуха, направление ветра, количество осадков);
воздуха, направление ветра, количество осадков);
2. физико-географических (рельеф местности, наличие растительности, качество почв).
Поскольку эти факторы изменяются случайным образом, то и изменение уровня носит случайный характер. Вследствие этого, для вычисления уровня, как и любых других гидрологических величин, могут быть использованы методы математической статистики и теории вероятности.
Режимы колебания уровней характеризуются вероятностью и обеспеченностью,
Вероятность р (относительная частота) представляет собой отношение числа дней n 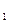 , когда наблюдается данный уровень к общему числу дней наблюдения
, когда наблюдается данный уровень к общему числу дней наблюдения 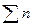 :
:
р = 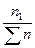
 .
.
Обеспеченность Р (относительная продолжительность) – это отношение числа дней, когда уровень был не ниже данного к общему числу дней:
Р= 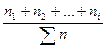
Ряды величин стока. Их характеристики.
Данные гидрологических наблюдений, например, величин стока за каждый год, выстраиваются в ряд, который представляет собой ряд случайных величин (М 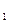 , М
, М 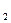 ,…,М
,…,М  ). Такой ряд, выстроенный в хронологическом порядке, называется вариационным рядом.
). Такой ряд, выстроенный в хронологическом порядке, называется вариационным рядом.
К характеристикам вариационного ряда относятся:
1. Среднее арифметическое значение:
М 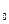 =
= 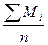 .
.
Такое среднее арифметическое значение ряда, которое не изменяется сколько-нибудь существенным образом при его удлинении, то есть при добавлении к нему новых данных, называется нормой и обозначается 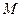 .
.
2 Что может характеризовать изменчивость ряда?
Среднее арифметическое отклонение:
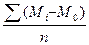 ,
,
не может являться такой характеристикой, так как оно все время будет равно нулю. Этого можно избежать, если возвести в квадрат числитель дроби:
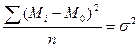
Если теперь извлечь из данного выражения квадратный корень, то мы получим величину среднего квадратичного отклонения или дисперсии:
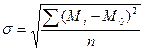 .
.
Размерность дисперсии 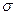 та же что и у членов ряда. Однако и дисперсия не может служить критерием изменчивости, если сравниваются между собой ряды с разными значениями среднего арифметического значения М
та же что и у членов ряда. Однако и дисперсия не может служить критерием изменчивости, если сравниваются между собой ряды с разными значениями среднего арифметического значения М 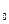 . Поэтому для сравнения различных рядов с разными средними арифметическими, используется относительное среднее квадратическое отклонение или коэффициент вариации (изменчивости):
. Поэтому для сравнения различных рядов с разными средними арифметическими, используется относительное среднее квадратическое отклонение или коэффициент вариации (изменчивости):
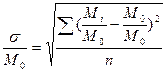 .
.
С учетом того, что 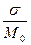 =
= 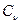 (коэффициент вариации), а
(коэффициент вариации), а 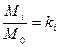 (модульный коэффициент), предыдущее выражение может быть представлено в виде:
(модульный коэффициент), предыдущее выражение может быть представлено в виде:
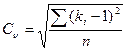 ,
,
где 1 – среднее значение модульного коэффициента 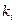 .
.
Поскольку n – число членов ряда в общем случае стремится к бесконечности, то, для того чтобы оперировать конечным числом членов ряда, в знаменатель подкоренного выражения вводится (-1):
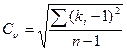
Если перестроить вариационный ряд в порядке убывания величин, то мы получим ранжированный ряд. Для ранжированного ряда через отношение порядкового номера члена ряда (m) к общему числу членов ряда может быть определена эмпирическая обеспеченность каждого члена ряда:
Р  =
= 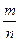 .
.
В данное выражение вводится поправка на +1 для того, чтобы обеспеченность даже самой маленькой величины никогда не равнялась 100%:
Р 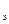 =
= 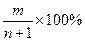 , (%)
, (%)
Зная эмпирическую обеспеченность каждого члена ранжированного ряда, можно построить эмпирическую кривую обеспеченности:
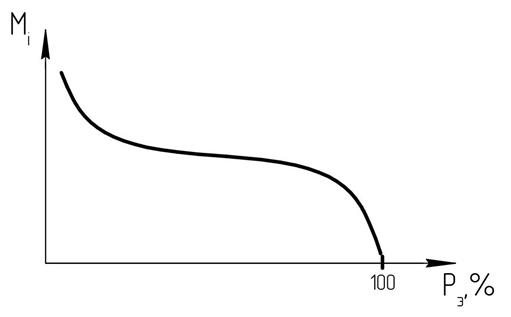 Рисунок 8
Рисунок 8
Эмпирическая кривая обеспеченности позволяет, пользуясь заданными значениями обеспеченности, получать интересующие нас значения той или иной гидрологической величины. Однако для того, чтобы иметь возможность оперировать имеющимися данными, мы должны знать, можно ли экстраполировать (распространять) имеющую информацию, делая прогноз на будущее. Для этого мы должны выяснить, является ли тот ряд данных, который мы использовали в расчете, представительным или репрезентативным. Это определяется по величине относительных средних квадратических ошибок:
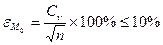 ;
;
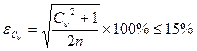
В том случае, если обе ошибки попадают в указанные для них пределы, то ряд наблюдений является достаточным или представительным (репрезентативным). Если хотя бы одна из ошибок выходит из указанных пределов, то ряд исходных данных является не представительным и по нему нельзя правильно определить искомые параметры. В этом случае ряд необходимо удлинить, то есть дополнить его новыми членами.
Кривые вероятности и обеспеченности.
Обычно число лет наблюдений за характеристиками стока ограничено и не охватывает весь диапазон возможных изменений случайной величины, поэтому, используя понятие ранжированного ряда и эмпирической обеспеченности, и строят эмпирическую кривую обеспеченности:
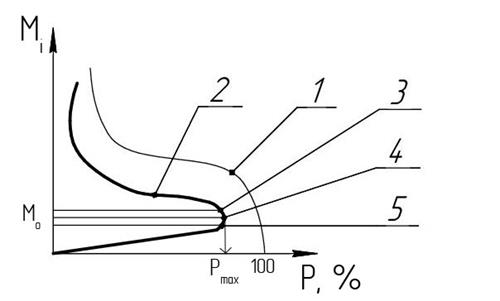
Рисунок 9
На рисунке изображены эмпирическая кривая обеспеченности и кривая распределения вероятности:
1 – эмпирическая кривая обеспеченности;
2 – кривая распределения вероятности (гистограмма);
3 – медиана;
4 – мода;
5 – центр распределения
Кривая распределения вероятности имеет три характерных точки:
- мода – точка, соответствующая максимальному значению вероятности;
- медиана, которая делит ряд на две равных части;
- центр распределения – точка, соответствующая среднему арифметическому значению ряда М  .
.
Ряд гидрологических величин на самом деле помимо средней величины М  , а также коэффициента вариации С
, а также коэффициента вариации С  характеризуется и коэффициентом ассиметрии С
характеризуется и коэффициентом ассиметрии С  . Таким образом кривые обеспеченности также характеризуются тремя основными параметрами:
. Таким образом кривые обеспеченности также характеризуются тремя основными параметрами:
- М – норма;
- С  ;
;
- С 
Используя эти параметры можно построить теоретическую кривую обеспеченности (ТКО). Математически были подобраны два вида кривых, которые наиболее близко соответствуют эмпирической кривой обеспеченности (ЭКО) и используются для построения ТКО. Это кривая трехпараметрического гамма распределения и биноминальная кривая. ТКО отличается от ЭКО:
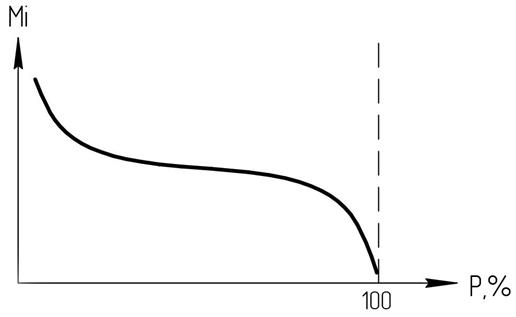
Рисунок 10
Если ЭКО может касаться оси ординат и вертикали, восстановленной из 100%, то ТКО асимптотически приближается к ним. Если бы ТКО касалась оси ординат, то это бы означало, что максимальное значение величины ряда никогда не может быть превышено, однако, в действительности это не правильно, поскольку и самая большая величина из ряда наблюдений в дальнейшем может превышаться.
Лекция 4: Метод наибольшего правдоподобия для построения ТКО.
Данный метод применяется при большой изменчивости ряда, когда С  >0,5. Для построения ТКО в этом методе применяется кривая трехпараметрического гаммараспределения. Имеем ряд гидрологических наблюдений М
>0,5. Для построения ТКО в этом методе применяется кривая трехпараметрического гаммараспределения. Имеем ряд гидрологических наблюдений М 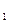 , М
, М 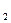 ,..,М
,..,М 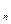 .
.
1. Определяем среднее арифметическое значение ряда:
М 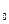 =
= 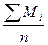 ;
;
2. Вычисляем модульный коэффициент:
k  =
= 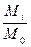 ;
;
3. Определяем статистики:
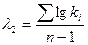 ( всегда отрицательная),
( всегда отрицательная),
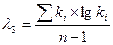 ( всегда положительная)
( всегда положительная)
4. По номограмме определяем значения коэффициента вариации С  и соотношение между коэффициентом вариации С
и соотношение между коэффициентом вариации С  и коэффициентом ассиметрии С
и коэффициентом ассиметрии С  :
:


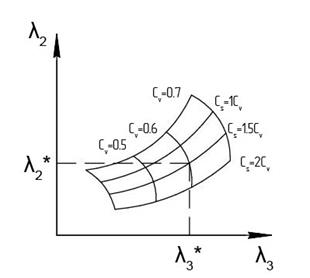
Рисунок 11
С  =0,6
=0,6
С  =1,5С
=1,5С 
5. Оцениваем представительность ряда по величине относительной средних квадратичных ошибок: 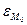 и:
и:
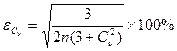
Если 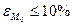 , а
, а 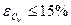 , то ряд является представительным и значит:
, то ряд является представительным и значит:
М 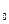 =М
=М
6. По таблицам СНиП определяем ординаты модульных коэффициентов ТКО по величине С  и соотношению между С
и соотношению между С  и С
и С  :
:
Таблица 1
Пример: С  =1,5С
=1,5С 
| Р,% | Коэффициенты С  | ||||
| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| 0,01 | Кр | ||||
| 0,1 | |||||
| 0,5 | |||||
| … | |||||
| 99,9 |
Интервал между значениями обеспеченности в первой колонке меньше между крайними значениями, чем между средними. Это объясняется тем, что кривая обеспеченности в своей средней части ближе к прямой линии, чем по краям, поэтому для точного построения ТКО и приходится интервал между крайними значениями уменьшать.
7. По величине модульных коэффициентов Кр, взятых из приведенной таблицы, рассчитываем непосредственно ординаты ТКО:
Мр = Кр×М
8. Строим ТКО и по заданному значению обеспеченности с ТКО определяем величину интересующегося нас гидрологического параметра.
Иногда для того, чтобы выпрямить кривую обеспеченности, при ее построении используются клетчатки со значительной асимметричностью, у которых начало и конец растянуты, а середина сжата. Применение таких клетчаток позволяет значительно повысить точность определения гидрологических параметров, соответствующих большим или малым значениям обеспеченности.
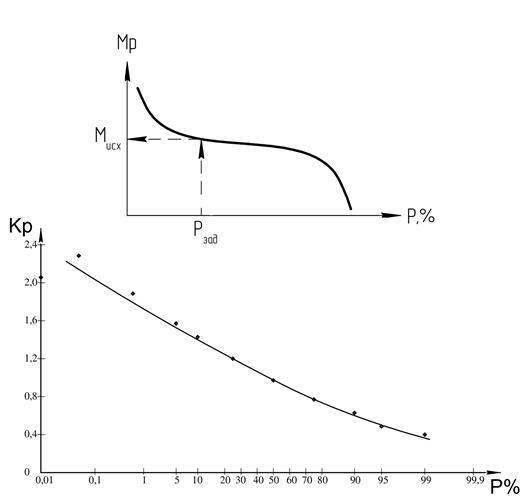
Рисунок 12
Метод моментов для построения ТКО.
Применяется при малой изменчивости ряда, когда С 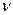 <0,5. Для построения ТКО используется биноминальная кривая.
<0,5. Для построения ТКО используется биноминальная кривая.
Имеем вариационный ряд наблюдений М  , М
, М  ,…,М
,…,М 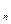 :
:
1. Определяем среднее арифметическое значение ряда: М 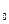 =
= 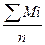 ;
;
2. Рассчитываем модульные коэффициенты: k  =
= 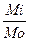 ;
;
3. Определяем разности между (k  -1) и (k
-1) и (k  -1)
-1) 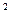 ;
;
4. Определяем: С  =
= 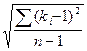 ;
;
5. Оцениваем представительность ряда:
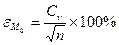 ;
;
Если 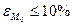 и
и 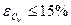 , то ряд данных является представительным и М
, то ряд данных является представительным и М 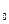 =М;
=М;
6. Задаемся соотношением между С  и С
и С  :
:
С  =АС
=АС  , где А – коэффициент пропорциональности, изменяющийся в пределах от 1 до 4(Аср.=2);
, где А – коэффициент пропорциональности, изменяющийся в пределах от 1 до 4(Аср.=2);
7. По таблице нормированных отклонений от средней биноминальной кривой определяем нормированные отклонения Фр:
Таблица 2
СС  | Обеспеченность Р, % | SS | |||||||||||
| 00,01 | 00,1 | 0,5 | з1,0 | 55,0 | .… | 999,9 | |||||||
| l0,1 | |||||||||||||
| 00,2 | |||||||||||||
| 00,4 | |||||||||||||
| 00,6 | |||||||||||||
| 00,8 | |||||||||||||
| 11,0 | |||||||||||||
| 2… |
8. Рассчитываем модульные коэффициенты: Кр=С  ×Фр+1;
×Фр+1;
9. Определяем ординаты ТКО: Мр = Кр×М;
10. Строим ТКО.
Перед тем, как использовать ТКО для определения искомой величины, нужно выяснить правильно ли мы задались соотношением между С  и С
и С  . Для этого вариационный ряд наблюдений перестраивается в ранжированный ряд:
. Для этого вариационный ряд наблюдений перестраивается в ранжированный ряд:
| m | … | N | |||
и для каждого члена ранжированного ряда определяется эмпирическая обеспеченность:
Рэ= 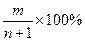 ,
,
где m – порядковый номер члена ряда.
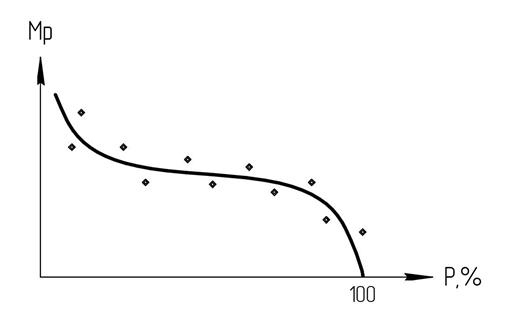
Рисунок 13
Полученные значения в виде точек наносятся на график ТКО. Если точки распределяются равномерно вдоль ТКО, а сама ТКО проходит через центры тяжести этих точек, то заданное нами соотношение между С  и С
и С  верно, а сама ТКО может использоваться для определения гидрологического параметра.
верно, а сама ТКО может использоваться для определения гидрологического параметра.
В противном случае необходимо задать новое соотношение между С  и С
и С  и все операции повторить.
и все операции повторить.
Графоаналитический метод построения ТКО.
Этот метод является универсальным, то есть применим при любых значениях коэффициента вариации С  . В качестве кривой обеспеченности используется биноминальная кривая.
. В качестве кривой обеспеченности используется биноминальная кривая.
Имеем вариационный ряд наблюдений: М 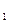 , М
, М 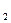 ,…,М
,…,М 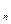 :
:
1. Вариационный ряд перестраиваем в ранжированный и для каждого члена ряда определяем эмпирическую обеспеченность:
Рэ = 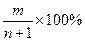 ;
;
2. Полученные точки наносим на график и по ним строим кривую обеспеченности;
3. По кривой обеспеченности определяем ординаты М 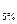 , М
, М 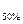 , М
, М 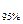 ;
;
4. Рассчитываем коэффициент скаженности s:
S= 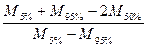 ;
;
5.По той же таблице, что и в методе моментов (таблица нормированных отклонений от средних ординат биноминальной кривой) определяем нормированное отклонение Ф 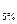 , Ф
, Ф 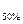 ,Ф
,Ф 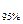 ;
;
6. Определяем дисперсию:
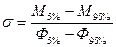 ;
;
7. Определяем коэффициент вариации:
С  =
= 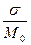 ,
,
где М 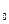 =М
=М 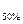 -
- 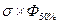
Таким образом мы имеем С  и С
и С  , которые взяли из таблицы в зависимости от коэффициента скаженности S;
, которые взяли из таблицы в зависимости от коэффициента скаженности S;
8. Оцениваем представительность ряда 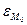 и
и 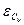 =
= 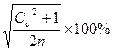 . Если
. Если 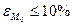 и
и 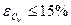 , то ряд данных является представительным, Мо=М. Следовательно, мы можем построить ТКО предварительно взяв из таблицы Фр, рассчитав далее Кр и Мр.
, то ряд данных является представительным, Мо=М. Следовательно, мы можем построить ТКО предварительно взяв из таблицы Фр, рассчитав далее Кр и Мр.
После этого, зная заданное значение обеспеченности. По ТКО находим интересующийся нас гидрологический параметр.
Лекция 5: Определение величин стока при недостаточности данных наблюдений. Аналоги. Корреляция.
Имеет место непредставительный короткий ряд данных. Необходимо найти величину стока заданной обеспеченности Мр. Для этого надо построить ТКО, а предварительно найти 3 параметра: М, С  , С
, С  .
.
Если ряд непредставительный, то для определения параметров ТКО используются данные, полученные на створе-аналоге.
Свойства аналога, по которым он определяется:
1. Должен быть расположен географически близко;
2. Должен иметь представительный (длинный) ряд наблюдений;
3.Должно наблюдаться сходство физико-географических и климатических условий;
4. Площадь бассейна аналога должна быть не меньше площади бассейна расчетного створа;
5. Должна наблюдаться синхронность колебаний стока;
6.Должны иметь место сходные факторы самого стока (степень дренирования подземных вод, степень занятости бассейна озерами, лесами, болотами);
7. Одинаковая степень обработки почвы.
Если эти данные для ряда совместных наблюдений нанести на график связи в виде точек, то провести на нем линию связи достаточно сложно.
Для выявления этой связи используется метод корреляции.
Корреляция – способ установления статистической связи между переменными величинами.
Статистическая связь – связь, при которой одному данному на аналоге соответствует несколько значений на расчетном створе.
Наряду со статистической связью, различают также функциональную связь – это связь, при которой одному значению на аналоге соответствует одно значение на расчетном створе.
Мерой тесноты выступает коэффициент корреляции ( 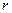 ):
):
r= 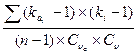 ,
,
где k 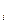 и k
и k 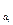 - модульные коэффициенты для расчетного створа и створа аналога;
- модульные коэффициенты для расчетного створа и створа аналога;
n – число лет совместных наблюдений;
С  и С
и С 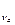 - коэффициенты вариации, рассчитываемые для створа аналога и расчетного створа:
- коэффициенты вариации, рассчитываемые для створа аналога и расчетного створа:
r=-1 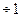
Если коэффициент корреляции =0, то связь между расчетным створом аналога отсутствует. Если r= 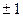 , то наблюдается однозначная функциональная связь.
, то наблюдается однозначная функциональная связь.
В гидрологии статистические методы могут быть использованы, если r 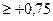 . При отрицательных значениях данные методы неприменимы, поскольку нарушается одно из требований выбора створа аналога, а именно, условие синхронного колебания стока. Определив r на графике, проводят прямые регрессии,
. При отрицательных значениях данные методы неприменимы, поскольку нарушается одно из требований выбора створа аналога, а именно, условие синхронного колебания стока. Определив r на графике, проводят прямые регрессии,
Прямая регрессии, проведенная таким образом, чтобы ординаты точек имели минимальное отклонение от нее, называются прямой регрессии данных на расчетном створе по данным на аналоге ( 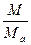 ).
).
Прямая регрессии, проведенная таким образом, чтобы абсциссы имели минимальное отклонение от нее, называется прямой регрессии данных на аналоге к данным на расчетном створе ( 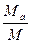 ).
).
Угол 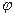 характеризует тесноту связи. Чем больше
характеризует тесноту связи. Чем больше 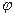 , тем меньше коэффициент корреляции r, и наоборот. При
, тем меньше коэффициент корреляции r, и наоборот. При 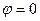 связь является функциональной (однозначной).
связь является функциональной (однозначной).
Уравнение прямой регрессии может быть представлено в виде:
М 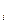 -М
-М 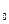 =R
=R 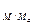 ×(M
×(M 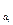 -V
-V 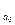 ),
),
где R 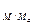 - коэффициент регрессии, который может быть определен как:
- коэффициент регрессии, который может быть определен как:
R 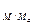 = r ×
= r × 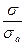 ;
; 
Определение параметров ТКО при недостаточных данных наблюдении:.
1. Осуществляется выбор аналога по указанным выше свойствам;
2. Определяется коэффициент корреляции r;
3. При условии, что r 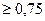 , осуществляется определение параметров ТКО.
, осуществляется определение параметров ТКО.
М определяется по уравнению прямой регрессии. При этом в уравнение вместо текущих значений подставляются соответствующие нормы:
М-М  =R
=R 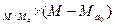 ,
,
отсюда:
М=М 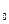 +R
+R 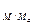 ×(M-M
×(M-M 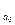 ),
),
где М 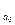 - среднеарифметическое значение данных на створе-аналоге для ряда основных наблюдений.
- среднеарифметическое значение данных на створе-аналоге для ряда основных наблюдений.
Далее:
1. рассчитывается по формуле С  ,
,
2. задаемся соотношением С  =А×С
=А×С  , где А применяется таким же как на створе-аналоге,
, где А применяется таким же как на створе-аналоге,
3. имея три параметра, мы можем найти ТКО и по ней найти гидрологический параметр, соответствующей заданной обеспеченности.
Определение расчетных гидрологических характеристик при отсутствии данных наблюдений.
Существует три способа определения параметров ТКО:
1. Норма М и С  определяются по изученным рекам методом интерполяции.
определяются по изученным рекам методом интерполяции.
Дано: М 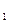 ; М
; М 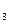 ; С
; С 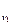 ; С
; С 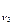 ; М
; М 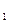 >М
>М 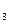
Найти: М 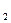 ; С
; С 
Решение:
 М
М  =М
=М  -
- 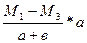
С 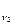 =С
=С 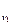 -
- 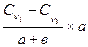

С 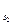 =АС
=АС 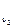
2. Определение осуществляется с помощью карт изолиний.
Изолиния– линия, которая проходит через точки с равными значениями гидрологических величин.
Имеются карты изолиний норм модулей стока М, слоев стока у, С 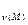 , С
, С 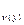 :
:
а) М=4 л/c×км 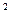 ;
;

б) в этом случае применяется метод интерполяции;

в) М= 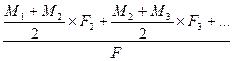
3. параметры ТКО определяют по региональным зависимостям:
С  =
= 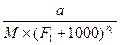 ,
,
где а – региональный коэффициент;
n 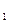 - показатель степени, равный 0,1
- показатель степени, равный 0,1
С  =АС
=АС  ,
,
где А – зависит от зоны, в зоне избыточного увлажнения А=2, в зоне достаточного увлажнения 1,5<A<1,7, для засушливых зон А=1,5.
Лекция 6: Оценка представительности рядов. Восстановление длинного ряда.
Существует три способа оценки представительности рядов:
1. Оценка проводится по величине средних квадратичных ошибок:
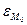 =
= 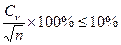
При С  >0,5 -
>0,5 - 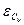 =
= 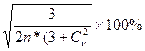
При С 
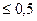 -
- 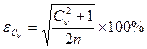 ;
;
Если указанные условия выполняются, то есть 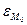
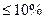 , а
, а 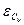
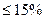 , то ряд исходных данных считается представительным и его среднее арифметическое значение соответствует норме: М
, то ряд исходных данных считается представительным и его среднее арифметическое значение соответствует норме: М 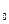 =М.
=М.
2. Оценка представительности ряда осуществляется на аналоге, если r 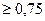 . Сравниваются между собой (по отдельности) значения С
. Сравниваются между собой (по отдельности) значения С  и С
и С  для длинного и короткого рядов на аналоге. Если расхождения между соответствующими коэффициентами не превышает 15%, то ряд данных на расчетном створе считается представительным.
для длинного и короткого рядов на аналоге. Если расхождения между соответствующими коэффициентами не превышает 15%, то ряд данных на расчетном створе считается представительным.
3. оценивается по разности интегральной кривой данных на аналоге при условии, что число лет наблюдений не менее 50.
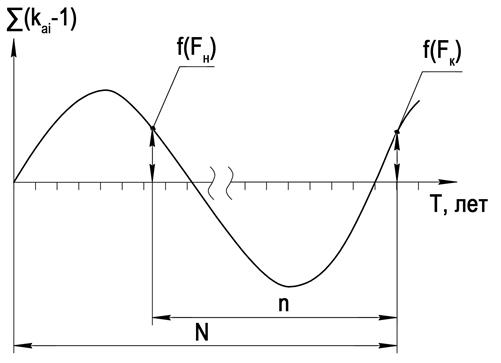
Рисунок 14
N – общее число лет наблюдений,
n – число лет совместных наблюдений
На тех участках разностной интегральной кривой, где 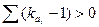 , показаны полноводные годы, где
, показаны полноводные годы, где 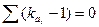 - средневодные годы, а где
- средневодные годы, а где 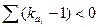 - маловодные годы.
- маловодные годы.
Если ординаты, ограничивающие ряд совместных наблюдений с его начала f (Fн) и конца f (Fk),равны между собой и между этими ними расположены средне-, много- и маловодные годы, то ряд данных на расчетном створе считается представительным (в нашем случае ряд непредставительный, так как n включает в себя только маловодные годы).
Если эти условия не выполняются, то ряд данных на расчетном створе является непредставительным и его необходимо удлинить.
Восстановление длинного ряда по данным наблюдений на створе-аналоге.
Существует три способа восстановления рядов:
1. По уравнению прямой регрессии:
М 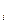 -М
-М 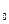 =R
=R 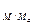 ×(M
×(M 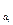 -M
-M  )
)
2. Используется при криволинейной зависимости график связи:
Рисунок 15
4. При условии, что коэффициент изменчивости для коротких рядов на расчетном створе и створе-аналоге расходятся больше чем на 20%, используется способ совмещения кривых обеспеченности, при которых обеспеченность величин стока за конкретные годы принимается одинаковой для обоих рядов. Эти кривые строят по правилам построения кривых при недостаточности данных наблюдений:
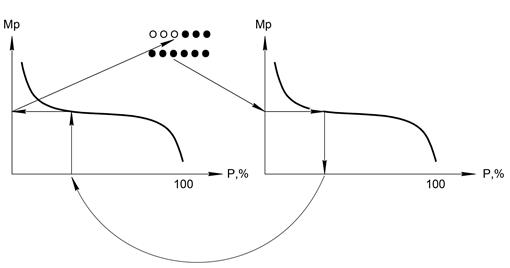
Рисунок 16
Внутригодовое распределение стока.
На внутригодовое распределение стока влияют климат, наличие болот, озер, лесов, хозяйственной деятельности человека. Задача внутригодового распределения стока состоит в том, чтобы определить величины стока заданной обеспеченности по расчетным отрезкам времени внутри года. За расчетные отрезки времени принимаются месяц, декада, неделя, сутки. В качестве расчетных величин используют, как правило, или средние расходы за расчетные отрезки времени или средние слои стока за расчетный отрезок времени. Возможны два вида представления исходных данных:
1. в виде календарных рядов;
2. в виде ранжированных рядов, то есть кривой обеспеченности.
Расчет осуществляется не по календарным, а по водохозяйственным годам.
Водохозяйственный год – это год, который начинается с первого числа первого полноводного месяца, при этом временные границы этого года определяются по данным наблюдений за все годы.
Водохозяйственный год, в свою очередь, делится на два периода:
1. лимитирующий;
2. нелимитирующий.
Причем лимитирующий период еще делится на:
а) лимитирующий сезон;
б) нелимитирующий сезон.
| Водохозяйственный год | ||
| Лимитирующий период | Нелимитирующий период | |
| Лимитирующий сезон | Нелимитирующий сезон | |
Лимитирующий сезон – это такой период времени, в течении которого имеют место неблагоприятные условия для работы проектируемого объекта.
Лекция 7: Расчет внутригодового распределения стока при наличии данных наблюдений.
Для расчетов используется два метода:
1. метод компоновки;
2. метод реального года
Метод компоновки применяется при числе лет более 10, если этот период включает в себя много- средне- и -маловодные годы. Он состоит из трех этапов:
1. Собственно компоновка.
