Светлячковый алгоритм применяется для решения класса задач непрерывной глобализации

Алгоритм роя частиц

Стая птиц летая большими группами, почти никогда не сталкиваются в воздухе. Дело тут отнюдь не в вожаке, отдающем приказы – в стаях многих видов птиц его просто нет. Как и колония муравьев или пчел, стая представляет собой роевой интеллект. Птицы в ней действуют согласно определенным – довольно простым – правилам. Кружа в небе, каждая из птиц следит за своими сородичами и координирует свое движение согласно их положению.

Наблюдение за птицами вдохновило Крейга Рейнольдса на создание в 1986 году компьютерной модели, которую он назвал Boids. Для имитации поведения стаи птиц, Рейнольдс запрограммировал поведение каждой из них в отдельности, а также их взаимодействие. При этом он использовал три простых принципа. Во-первых, каждая птица в его модели стремилась избежать столкновений с другими птицами. Во-вторых, каждая птица двигалась в том же направлении, что и находящиеся неподалеку птицы. В-третьих, птицы стремились двигаться на одинаковом расстоянии друг от друга.

Результаты первых же симуляций удивили самого создателя: несмотря на простоту лежащих в основе программы алгоритмов, стая на экране выглядела крайне правдоподобно.

Классический алгоритм роя частиц. В 1995 году Джеймс Кеннеди и Рассел Эберхарт предложили метод для оптимизации непрерывных нелинейных функций, названный ими алгоритмом роя частиц. Вдохновением для них послужила имитационная модель Рейнольдса.

Разработанный ими алгоритм довольно прост и может быть реализован буквально в нескольких десятках строчек кода на любом высокоуровневом языке программирования. Он моделирует много агентную систему, где агенты-частицы двигаются к оптимальным решениям, обмениваясь при этом информацией с соседями.

Чтобы понять алгоритм роя частиц, представьте себе n-мерное пространство (область поиска), в котором рыщут частицы (агенты алгоритма). В начале частицы разбросаны случайным образом по всей области поиска и каждая частица имеет случайный вектор скорости. В каждой точке, где побывала частица, рассчитывается значение целевой функции. При этом каждая частица запоминает, какое (и где) лучшее значение целевой функции она лично нашла, а также каждая частица знает где расположена точка, являющаяся лучшей среди всех точек, которые разведали частицы. На каждой итерации частицы корректируют свою скорость (модуль и направление), чтобы с одной стороны быть поближе к лучшей точке, которую частица нашла сама (авторы алгоритма назвали этот аспект поведения "ностальгией"), и, в то же время, приблизиться к точке, которая в данный момент является глобально лучшей. Через некоторое количество итераций частицы должны собраться вблизи наиболее хорошей точки, хотя возможно, что часть частиц останется где-то в относительно неплохом локальном экстремуме, но главное, чтобы хотя бы одна частица оказалась вблизи глобального экстремума.

На каждой итерации алгоритма направление и длина вектора скорости каждой из частиц изменяются в соответствие со сведениями о найденных оптимумах: 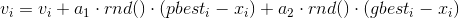, (1)
где – вектор скорости частицы ( 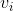– его i-ая компонента), 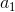, 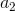– постоянные ускорения, 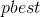– лучшая найденная частицей точка, 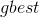– лучшая точка из пройденных всеми частицами системы, 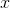– текущее положение частицы, а функция 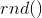возвращает случайное число от 0 до 1 включительно.

После вычисления направления вектора , частица перемещается в точку 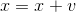. В случае необходимости, обновляются значения лучших точек для каждой частицы и для всех частиц в целом. После этого цикл повторяется.

Блок-схема алгоритма выглядит следующим образом:

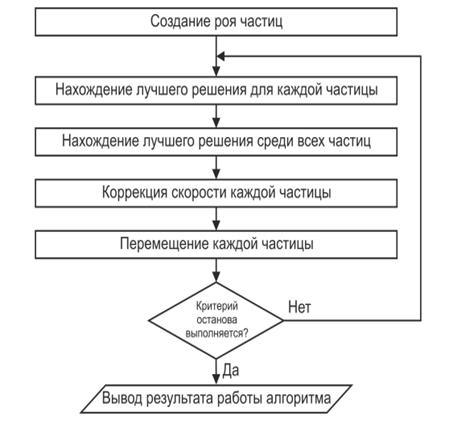
Модификации классического алгоритма.Алгоритм роя частиц появился относительно недавно, однако различными исследователями уже был предложен целый ряд его модификаций, и новые работы на эту тему не перестают публиковаться. Можно выделить несколько путей улучшения классического алгоритма, реализованных в большинстве из них. Это соединение алгоритма с другими алгоритмами оптимизации, уменьшение вероятности преждевременной сходимости путем изменения характеристик движения частиц, а также динамическое изменение параметров алгоритма во время оптимизации.

Алгоритм роя частиц широко применяется, в задачах машинного обучения (в частности, для обучения нейросетей и распознавания изображений), параметрической и структурной оптимизации (форм, размеров и топологий) в области проектирования, в областях биохимии и биомеханики.

Недостаток алгоритма в том, что, не гарантирована сходимость алгоритма при конечном числе частиц, и, что характерно для этого алгоритма, - это ориентация на одну лучшую точку, что увеличивает вероятность остановки алгоритма в неплохом, но не глобальном минимуме.

Метод имитации отжига

Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Предложенный Н. Метрополисом в 1953 г. и доработанный многочисленными последователями, он в настоящее время считается одним из немногих алгоритмов, позволяющих практически находить глобальный минимум функции нескольких переменных.

Метод имитации отжига основан на идее, заимствованной из статической механики. Он отражает поведение материального тела при отвердевании с применением процедуры отжига (управляемого охлаждения) при температуре, последовательно понижаемой до нуля. Как показали исследования, при отвердевании расплавленного материала его температура должна уменьшаться постепенно, вплоть до момента полной кристаллизации. Если процесс остывания протекает слишком быстро, образуются значительные нерегулярности структуры материала, которые вызывают внутренние напряжения. В результате общее энергетическое состояние тела, зависящее от его внутренней напряженности, остается на гораздо более высоком уровне, чем при медленном охлаждении. Быстрая фиксация энергетического состояния тела на уровне выше нормального аналогична сходимости оптимизационного алгоритма к точке локального минимума. Энергия состояния тела соответствует целевой функции, а абсолютный минимум этой энергии - глобальному минимуму.

При помощи моделирования процесса отжига ищется такая точка или множество точек, на котором достигается минимум некоторой числовой функции 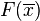, где 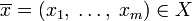. Решение ищется последовательным вычислением точек 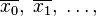пространства 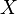; каждая точка, начиная с 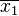, «претендует» на то, чтобы лучше предыдущих приближать решение. Алгоритм принимает точку 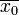как исходные данные. На каждом шаге алгоритм (подробное описание ниже) вычисляет новую точку и понижает значение величины (изначально положительной), понимаемой как «температура». Алгоритм останавливается по достижении точки, которая оказывается при температуре ноль.

Алгоритм имитации отжига похож на градиентный спуск, но за счёт случайности выбора промежуточной точки должен будет попадать в локальные минимумы реже, чем градиентный спуск. Алгоритм имитации отжига не гарантирует нахождения минимума функции, однако при правильной политике генерации случайной точки в пространстве 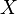, как правило, происходит улучшение начального приближения.

Общий вид алгоритма имитации отжига представлен на рисунке.

Далее более подробно рассмотрим все шаги алгоритма.

1. Выбор начального решения, начальной и пороговой температур. Хорошей стратегий является случайный выбор начального решения, либо в качестве него можно предложить решение, полученное другими методами. Выбор начальной и пороговой температуры следует производить экспериментально. Естественными рекомендациями могут служить выбор пороговой температуры близкой к нулю, а начальной достаточно высокой.

2. Оценка решения. Вычисление значения целевой функции в точке, соответствующей текущему решению. (Это число в алгоритме имитации отжига принято называть энергией.)

3. Основной шаг алгоритма. Основной шаг при некоторой температуре повторяется несколько раз (возможно, один раз). Также возможен вариант с зависимостью числа повторов от температуры.

3.1. Случайное изменение решения. Нахождение новой точки случайным образом. Изменения стоит производить локальные. В результате изменения у нас будет два решения: текущее и измененное.

3.2. Критерий допуска. Критерий допуска заключается в проверке и возможной замене текущего решения измененным.

Если измененное решение имеет меньшую энергию (значение целевой функции меньше), то оно принимается за текущее. Если же измененное решение имеет бОльшую энергию, то оно принимается с вероятностью

P = exp(-δE/T), где:

P — вероятность принять измененное решение,

δE — модуль разности между энергией оптимального решения и энергией измененного решения,

T — текущая температура.

4. Уменьшение температуры. Выбор способа уменьшения температуры может быть различным и выбирается экспериментально. Главное, чтобы температура монотонно убывала к нулю. Хорошей стратегий является умножение на каждом шаге температуры на некоторый коэффициент немного меньший единицы (от 0,7 до 0,99).

При достижении Т=0 полученное решение принято считать лучшим (глобальным минимумом).

К настоящему времени разработано множество различных вариантов метода отжига, как общих, так и их специализаций для конкретных задач. Их различия состоят в выборе:

1) вероятностного распределения для нахождения случайного решения;

2) закона убывания температуры;

3) критерия допуска (вероятности того, что полученное решение станет рабочим).

Например: Больцмановский отжиг – нормальное распределение; изменение температуры: T(k) = T₀/ ln(1 + k), k > 0 (где k – шаг алгоритма)

Отжиг Коши – распределение Коши, изменение температуры – аналогично.

Метод «тушения» - нормальное распределение (из Больцмановского отжига), изменение температуры T_k+1 = cT_k. (где 0,7< c < 0.99).

В настоящее время метод отжига применяется для решения многих оптимизационных задач – финансовых, компьютерной графики, комбинаторных, в телекоммуникационных сетях, и многих других. Зачастую метод отжига используют для обучения нейронных сетей. К областям применения относятся:

· создание пути (в т.ч. задача коммивояжера);

· реконструкция изображения;

· назначение задач и планирование;

· размещение сети;

· глобальная маршрутизация (транспорт);

· обнаружение и распознавание визуальных объектов;

· разработка специальных цифровых фильтров.

Рассматривая данный вопрос, нельзя не упомянуть преимущества и недостатки применения метода имитации отжига.

Преимущества:

· отсутствие ограничений на вид минимизируемой функции;

· поиск глобального минимума;

· эффективность при решении задач различных классов, требующих оптимизации.

Недостатки:

· требование бесконечно медленного охлаждения, на практике означающее медленную работу алгоритма;

· сложность настройки (выбор параметров, пороговых температур и т.д.).

26. Алгоритм интеллектуальной оптимизации «Оптимизация передвижением бактерий».

Биологические основы. Одной из наиболее изученных бактерий является бактерия E.Coli. Живёт в кишечнике большинства млекопитающих, самовоспроизводиться за 20 мин, способность двигаться обеспечивается за счёт жгутиков мотора.

Бактерия E.Coli чередует свои действия: то перемещается прямолинейно, то кувыркается (изменение направления).

Хемотаксис – это двигательная реакция бактерии в ответ на появление в среде аттрактанта (аттрактант – вещество, привлекающее бактерии) или репеллента (репеллент – вещество, отпугивающее бактерий).

Примерная схема движения бактерии выглядит следующим образом: когда мотор работает в одну сторону, все жгутики у бактерии складываются и крутятся вместе, и бактерия движется прямолинейно. В конце пробега бактерия останавливается, мотор переключается и начинает работать в другую сторону. Бактерия при этом переориентируется в пространстве случайным образом. После этого, мотор опять переключается и начинает работать в ту сторону, в которую жгутики работают вместе, и возникает следующий отрезок прямолинейного движения.

Таким образом, можно выделить следующие хемотаксические действия бактерии E.Coli:

– если бактерия находится в нейтральной среде, то чередуются кувырки и передвижения, за счёт чего выполняется поиск.

– если бактерия перемещается по градиенту аттрактанта, то перемещение продолжается в этом же направлении. Таким образом, обеспечивается поиск более благоприятной окружающий среды.

– если происходит перемещение в направлении противоположном градиенту репеллента, то обеспечивается избегание неблагоприятной окружающей среды.

Бактерии часто умирают или растворяются, и это должно учитываться при моделировании их деятельности. Мутации у E. coli происходят в нормальных условиях приблизительно 10−7 в ген и в поколение.

E.Coli могут формировать сложные устойчивые пространственно-временные структуры в некоторых полутвердых полезных средах. Бактерии могут поглощать питательные вещества по их радиусу, начиная от внешней границы, заканчивая серединой, даже в случае если бактерии были изначально размещены в центре питательных веществ. Кроме того, при определённых условиях, они могут скрывать притягивающие сигналы от клетки к клетке, за счёт чего они группируются и защищают друг друга. Таким образом, эти бактерии могут группироваться в колонии.

Метод оптимизации на основе моделирования перемещения бактерий (BacterialForagingOptimization, BFO)

Данный метод предназначен для нахождения минимума функции J(X), X∈Rp при неизвестном градиенте ∇J(X), где X – позиция бактерии в пространстве поиска Rp, а с помощью J(θ) моделируются полезные и вредные свойства среды, т.е. J(X) характеризует, где находятся аттрактанты и репелленты. Таким образом, J<0, J=0, J>0 означает, что бактерия находится в полезной, нейтральной и вредной среде, соответственно.

Пусть P(j, k, l ) = {Xi( j, k, l ) , i=1, 2, … , S} описывает позицию каждого члена популяции S бактерий на j-ом хемотаксическом шаге, k-ом шаге воспроизведения и на l-ом событии исключения- рассеивания.

Тогда работу метода оптимизации с помощью моделирования фуражировки бактерий можно представить в виде последовательности выполнения следующих шагов.

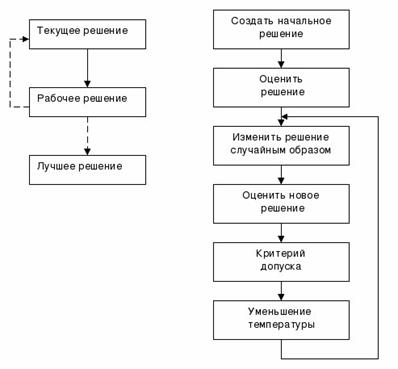
Шаг 1. Инициализация. Задаются параметры, влияющие на работу метода: S – количество бактерий, Nre – количество шагов воспроизведения, Ns – количество шагов-повторений на одном хемотаксическом шаге, Nc – количество хемотаксических шагов, Ned – количество событий исключения-рассеивания; Ped – вероятность рассеивания. Случайным образом распределить начальные значения Xi, i = 1, 2, ..., S по пространству поиска. Рассчитываются начальные значения целевой функции для каждой бактерии Ji.

Шаг 2. Установить: l = l + 1. Шаг 3. Установить: k = k + 1. Шаг 4. Установить: j = j + 1.

Шаг 5. Для каждой бактерии моделируется хемотаксис: кувыркание, перемещение и скольжение.

Шаг 5.1. Установить: i = i + 1.

Шаг 5.2. Кувыркание. Моделирование кувыркания достигается за счёт генерации вектора случайных чисел φ(j) ∈Rp: где – вектор случайных чисел в интервале [–1; 1].

Вектор φ представляет собой множество длин для соответствующих измерений.

Шаг 5.3. Перемещение. Рассчитывается новое положение i-ой бактерии по формуле:

Xi(j+1, k, l) = Xi(j, k, l)+C(i)φ(j),

где C(i)>0 – размер шага в определённом направлении, позволяющий моделировать процесс кувыркания.

Для новой позиции Xi(j+1, k, l) рассчитывается соответствующее значение целевой функции J(i, j+1, k, l).

Шаг 5.4. Скольжение. Если в позиции Xi(j+1, k, l ) значение J(i, j+1, k, l) лучше, чем в позиции Xi(j, k, l), то есть выполняется условие: J(i, j+1, k, l) < J(i, j, k, l), тогда производится следующий хемотаксический шаг с тем же вектором φ и в том же направлении (переход к шагу 5.3), и такое повторение может повторяться Ns раз. Если условие не выполняется, то переход к шагу 5.5.

Шаг 5.5 Если i<S, то переход к шагу 5.1, в противном случае – переход к шагу 6.

Шаг 6. Если j <Nc, то переход к шагу 4, в противном случае – переход к шагу 7.

Шаг 7. Воспроизведение. Менее здоровые бактерии умирают, а остальные, более здоровые, разделяются на две бактерии, при этом новые бактерии размещаются в ту же самую точку пространства поиска. За счёт такого подхода обеспечивается неизменность общего количества бактерий. Для этого все агенты сортируются в соответствии с полученными значениями целевой функции, после чего худшая половина (менее здоровые бактерии) отбрасывается, а лучшая (более здоровые бактерии) – дублируется.

Шаг 8. Если k <Nre, тогда выполняется переход к шагу 3, в противном случае – переход к шагу 9.

Шаг 9. Исключение и рассеивание. Жизнь популяции бактерий в окружающей среде может меняться либо постепенно (например, путём потребления полезных веществ), либо внезапно в связи с некоторым другим воздействием. Может произойти так, что все бактерии в области погибнут, или колония бактерий будет рассеяна в другую часть окружающей среды. Данный эффект может помешать возможному хемотаксическому прогрессу, но в то же время этот эффект и помогает, поскольку, в случае рассеивания, бактерии могут разместиться около хороших источников с полезными веществами. Исключение и рассеивание помогают понизить вероятность стагнации, то есть зацикливания в локальном оптимуме, что часто наблюдается в традиционных методах оптимизации (например, метод Коши, Ньютона, Левенберга-Марквардта и т.п.).

В соответствии с данным подходом каждая бактерия с вероятностью Ped размещается в случайно выбранной точке пространства поиска.

Таким образом, проверяется условие: Ui<Ped, где Ui – случайное число в интервале [0; 1] для i-ой бактерии.

Если данное условие выполняется, то бактерия помещается в позицию Xi(j, k, l), полученную случайным образом.

Шаг 10. Если l <Ned, тогда выполняется переход к шагу 2, в противном случае – к шагу 11.

Шаг 11. Выбирается и сохраняется лучшее решение Jbest и соответствующая позиция Xbest, в которой достигается лучшее решение Jbest.

Шаг 12. Проверка на окончание поиска. Если были выполнены все циклы для всех агентов, то выполняется переход к шагу 14, в противном случае выполняется перезапуск – переход к шагу 13.

Шаг 13. Перезапуск агентов: выбираются новые случайные позиции для каждого агента Xi, i = 1, 2, ..., S и рассчитываются соответствующие значения целевой функции Jⁱ, i = 1, 2, ..., S. Счётчики циклов сбрасываются в 0: j = 0; k = 0; l = 0.

Шаг 14. Остановка.

Общая схема работы метода оптимизации на основе моделирования перемещения бактерий представлена на рис.1.

Рассмотренный метод оптимизация на основе моделирования перемещения бактерий не учитывал одну из важных особенностей поведения бактерий: бактерии E.Coli, как указывалось ранее, способны, группируясь, создавать пространственно-временные структуры. В связи с этим было предложено несколько подходов, позволяющих учитывать в процессе моделирования перемещения бактерий и данную особенность их поведения, основными из которых являются: моделирование сигналов между клетками и применение PSO-оператора (ParticleSwarmOptimization, PSO).

27. Алгоритм интеллектуальной оптимизации «Алгоритм летучей мыши».

Общая характеристика алгоритма.Алгоритмы роевого интеллекта – это алгоритмы коллективного поведения децентрализованных, самоорганизующихся естественных или искусственных систем. Данные алгоритмы получили свое начало в 1989 году, когда ХерардоБени и Ван Цзин ввели данный термин в контексте системы клеточных роботов.

Алгоритм летучих мышей (BatAlgoithm) – это алгоритм оптимизации, разработанный Янгом (X.-Sh.Yang) в 2010 году. Одним из основных преимуществ алгоритма является скорость его выполнения. Этот алгоритм потенциально более мощный, чем алгоритм роя частиц и генетический алгоритм, а так же гармонический поиск. Более того, гармонический поиск и алгоритм роя частиц являются особыми случаями алгоритма летучих мышей при соответствующих упрощениях.Алгоритм может показаться немного сложнее, чем большинство других алгоритмов роевого интеллекта, а также эволюционных алгоритмов, однако он может быть достаточно эффективно применен к проблемам оптимизации и давать хорошие результаты, затрачивая меньшее количество времени.

Описание алгоритма.Большинство видов летучих мышей обладает совершенными средствами эхолокации, которые используются ими для обнаружения добычи и препятствий, а также для обеспечения возможности разместиться в темноте на насесте.

Алгоритм летучих мышей подчиняется следующим правилам:

- Все летучие мыши используют эхолокацию, чтобы анализировать расстояние, а также иметь различие между едой (добычей) и природными препятствиями;

- Летучие мыши перемещаются случайным образом со скоростью V_i в позиции x_i с фиксированной частотой f_min, изменяемой длиной волны λ и громкостью А₀, чтобы найти добычу. Они могут автоматически регулировать длину волны (или частоту, т.к. частота = 1/длина волны) испускаемого импульса и скорость импульса rÎ [0,1], зависящих от близости цели.

- Громкость изменяется от большего (положительного) А₀ к меньшему постоянному значению А_min .

Схема алгоритма может быть представлена в виде последовательности шагов:

Шаг 1. Определение объективной функции f(x), x=(x₁…x_d)^T.

Шаг 2. Инициализация исходной популяции летучих мышей x_i (i=1…n), скорости летучих мышей v_i, громкости A_i, скорости распространения импульса r_i.

На данном шаге задается начальное положение летучей мыши, т.е. случайный вектор, который и является текущим решением. Также указываются начальные значения громкости, скорости распространения импульса и числа итераций.

Шаг 3. Определение частоты испускаемого импульса f_i в x_i.

Шаг 4. Определение оптимума, т.е. текущего лучшего решения.

Шаг 5. Генерация нового решения регулированием частоты и обновлением скорости и положения:

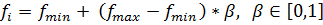(1)

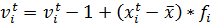(2)

где 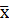- текущее лучшее положение.

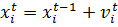(3)

Шаг 6. Генерация локального решения при условии, что случайно заданное число rand в интервале (0,1) больше скорости распространения импульса (rand>r_i):

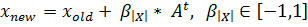(4)

где 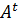– среднее значение громкости.

Шаг 7. Если локальное решение меньше, чем текущее лучшее решение, и случайное заданное число rand в интервале (0,1) меньше, чем громкость (rand>A_i), принимается новое решение, а также понижается громкость, и увеличивается скорость распространения импульса:

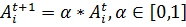(5)

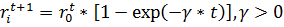
Шаг 8. В случае нахождения оптимума целевой функции прекращается работа алгоритма, иначе повторяются шаги 5 – 7, пока не закончены итерации.

Шаг 9. Вывод результатов и визуализация.

Преимущества и недостатки алгоритма летучей мыши.Преимуществами алгоритма являются:

· масштабируемость, возможность решать задачи независимо от их размерности;

· гибкость, системы не имеют жесткой структуры, могут без изменений использоваться с совершенно различных областях;

· удобство в применении к задачам с динамически изменяющимися условиями;

· эффективность решения оптимизационных задач.

Недостатки алгоритма заключаются в следующем:

· обычно необходимо применение дополнительных методов таких, как локальный поиск;

· сильно зависит от настройки параметров, которые подбираются только исходя из экспериментов.

Применение алгоритма летучей мыши.Рассмотренный алгоритм может быть применен для решения задач оптимизации, проектирования, планирования, классификации, решения проблемы эргономики рабочего места и др.

Алгоритм может быть применен в следующих областях:

Ø производственные системы;

Ø разработка программного обеспечения;

Ø системы массового обслуживания;

Ø все сферы применения управления проектами.

Модификации алгоритма.Модификации алгоритма летучей мыши

Модификация	Год создания	Предназначение
BAT-FLANN		для классификации данных по экспрессии генов
Directed Artificial Bat Algorithm (DABA)		для моделирования эхо системы летучих мышей
BinaryBatAlgorithm(BBA)		для решения двоичных задач