Аксонометрические проекции геометрических тел.
Понятие о проектировании
Изображения предметов на чертежах получают проецированием.
Проецирование есть процесс построения изображения предмета на плоскости при помощи проецирующих лучей. В результате этого процесса получается изображение, называемое проекцией.
Слово "проекция" в переводе с латинского означает бросание вперед, вдаль. Проекцию можно наблюдать, рассматривая тень, отбрасываемую предметом на поверхность стены при освещении этого предмета источником света.
Плоскостью проекций называют плоскость, на которой получают проекцию предмета.
Аксонометрия - слово греческое, в переводе означает измерение по осям.
При построении аксонометрических проекций размеры откладывают вдоль осей х, у, z.
Аксонометрические проекции отличаются наглядностью. Поэтому аксонометрические проекции применяют в тех случаях, когда требуется наглядность.
ГОСТ 2.317-69 (СТ СЭВ 1979-79) устанавливает пять видов аксонометрических проекций. Рассмотрим два наиболее употребительных вида.
v Изометрическая проекция
v Фронтальная диметрическая проекция
Правила построения изометрической и фронтальной диметрической
проекций одинаковы. Разница лишь в расположении осей и в длине отрезков, откладываемых вдоль оси y. Во фронтальной диметрической проекции вдоль оси х откладывают половину размера.
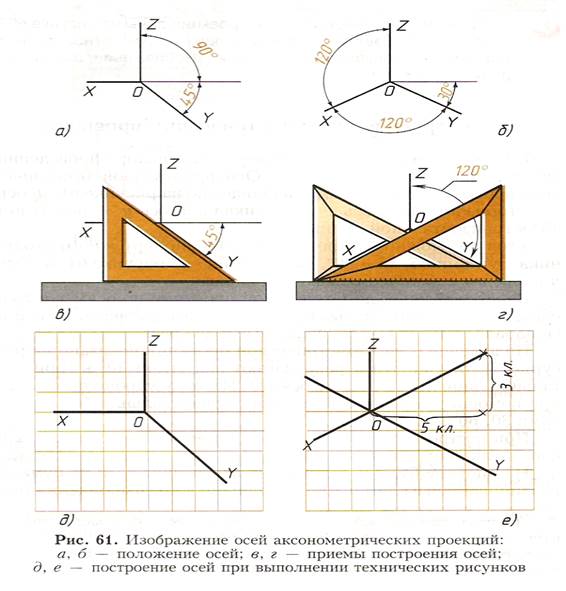
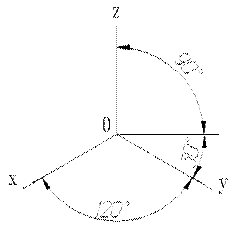 Рисунок 1. Расположение аксонометрических осей прямоугольной изометрической проекции Рисунок 1. Расположение аксонометрических осей прямоугольной изометрической проекции | Изометрическая проекция Положение аксонометрических осей приведено на рис.1. | |
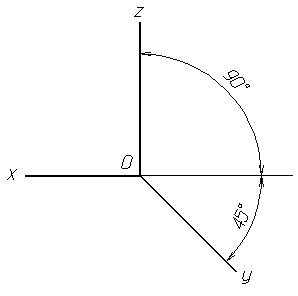 Рисунок 7. Расположение аксонометрических осей фронтальной изометрической проекции Рисунок 7. Расположение аксонометрических осей фронтальной изометрической проекции | Фронтальная диметрическая проекция Положение аксонометрических осей приведено на рис.7. Диметрическую проекцию, как правило, без искажения по осям x и z и с коэффициентом искажения 0.5 по оси y. |
2. Изометрические проекции окружностей. Изометрической проекцией окружности (рис. 65) является кривая, которая называется эллипсом. Эллипсы строить трудно. В практике черчения вместо них часто строят овалы. Овал — замкнутая кривая, очерченная дугами окружностей. Овал удобно строить, вписывая в ромб, который является изометрической проекцией квадрата. 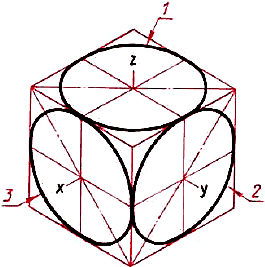 Рис. 65. Изображение в изометрической проекции окружностей вписанных в куб Построение овала, вписанного в ромб, выполняют в такой последовательности. Вначале строят ромб со стороной, равной диаметру изображаемой окружности (рис. 66, а). Для этого через точку О проводят изометрические оси х и у. На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с и d проводят прямые, параллельные осям; получают ромб. Рис. 65. Изображение в изометрической проекции окружностей вписанных в куб Построение овала, вписанного в ромб, выполняют в такой последовательности. Вначале строят ромб со стороной, равной диаметру изображаемой окружности (рис. 66, а). Для этого через точку О проводят изометрические оси х и у. На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с и d проводят прямые, параллельные осям; получают ромб. 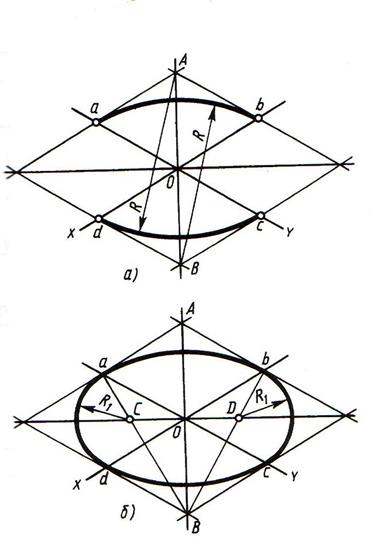 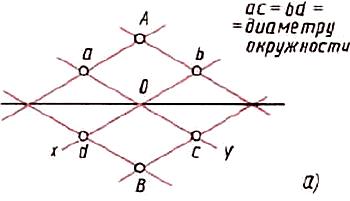 Рис. 66. Построение овала Большая ось овала располагается на большой диагонали ромба. После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги. Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек с, d или a, b соответственно (рис. 66, б). Через точки В и а, В и b проводят прямые. В пересечении прямых Ва и ВЬ с большей диагональю ромба находят точки С и D (рис. 66, а). Эти точки будут центрами малых дуг. Их радиус R1 равен Са (или Db). Дугами этого радиуса плавно соединяют большие дуги овала. Мы рассмотрели построение овала, лежащего в плоскости, перпендикулярной оси z (овал 1 на рисунке 65). Овалы, находящиеся в плоскостях, перпендикулярных оси у (овал 2) и оси х (овал 3), строят также. Только для овала 2 построение ведут на осях х и z (рис. 67, а), а для овала 3— на осях у и z (рис. 67, б). Рассмотрим, как применяются изученные построения на практике. Рис. 66. Построение овала Большая ось овала располагается на большой диагонали ромба. После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги. Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек с, d или a, b соответственно (рис. 66, б). Через точки В и а, В и b проводят прямые. В пересечении прямых Ва и ВЬ с большей диагональю ромба находят точки С и D (рис. 66, а). Эти точки будут центрами малых дуг. Их радиус R1 равен Са (или Db). Дугами этого радиуса плавно соединяют большие дуги овала. Мы рассмотрели построение овала, лежащего в плоскости, перпендикулярной оси z (овал 1 на рисунке 65). Овалы, находящиеся в плоскостях, перпендикулярных оси у (овал 2) и оси х (овал 3), строят также. Только для овала 2 построение ведут на осях х и z (рис. 67, а), а для овала 3— на осях у и z (рис. 67, б). Рассмотрим, как применяются изученные построения на практике. 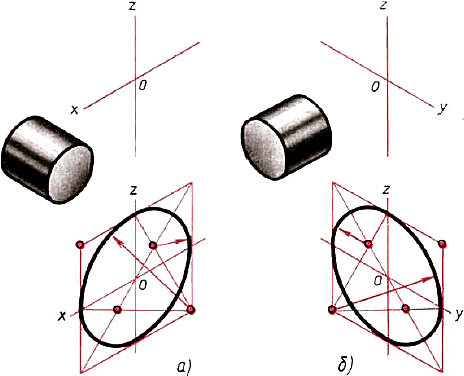 Рис. 67. Построение овалов: а лежащего в плоскости, перпендикулярной оси у; б — лежащего в плоскости, перпендикулярной оси x Задание для упражнения: Постройте овалы, соответствующие проекциям окружностей, вписанных в грани куба, данного в изометрической проекции (по примеру на рисунке 65). Сторона куба равна 60 мм. Рис. 67. Построение овалов: а лежащего в плоскости, перпендикулярной оси у; б — лежащего в плоскости, перпендикулярной оси x Задание для упражнения: Постройте овалы, соответствующие проекциям окружностей, вписанных в грани куба, данного в изометрической проекции (по примеру на рисунке 65). Сторона куба равна 60 мм. |
Аксонометрические проекции геометрических тел.
Проецирование правильных треугольной и шестиугольной призм. Основания призм, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях -- отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых на тех, которым они перпендикулярны (рис. 78). Грани. наклоненные к плоскостям проекций, изображаются на них искаженными. 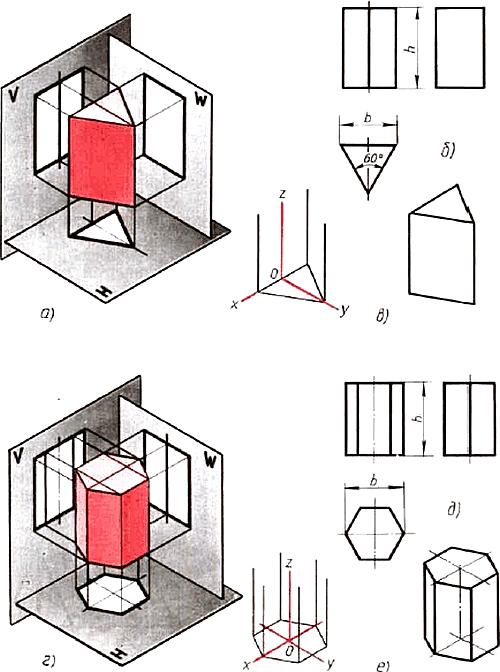 Рис 78. Призмы: а. г — проецирование; б, д — чертежи в системе прямоугольных проекции: в, с - изометрические проекции Размеры призм определяются их высотой и размерами фигуры основания. Штрихпунктирнымн линиями на чертеже проведены оси симметрии. Строить изометрические проекции призмы начинают с основания. Затем из каждой вершины основания проводят перпендикуляры, на которых откладывают отрезки, равные высоте, и через полученные точки проводят прямые, параллельные ребрам основания. Чертеж в системе прямоугольных проекций также начинают выполнять с горизонтальной проекции. Проецирование правильной четырехугольной пирамиды. Квадратное основание пирамиды проецируется на горизонтальную плоскость Н в натуральную величину. На нем диагоналями изображаются боковые ребра, идущие от вершин основания к вершине пирамиды (рис. 79). Рис 78. Призмы: а. г — проецирование; б, д — чертежи в системе прямоугольных проекции: в, с - изометрические проекции Размеры призм определяются их высотой и размерами фигуры основания. Штрихпунктирнымн линиями на чертеже проведены оси симметрии. Строить изометрические проекции призмы начинают с основания. Затем из каждой вершины основания проводят перпендикуляры, на которых откладывают отрезки, равные высоте, и через полученные точки проводят прямые, параллельные ребрам основания. Чертеж в системе прямоугольных проекций также начинают выполнять с горизонтальной проекции. Проецирование правильной четырехугольной пирамиды. Квадратное основание пирамиды проецируется на горизонтальную плоскость Н в натуральную величину. На нем диагоналями изображаются боковые ребра, идущие от вершин основания к вершине пирамиды (рис. 79). 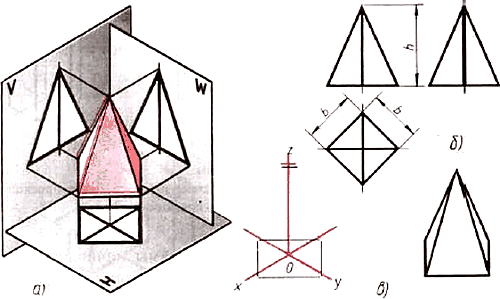 Рис. 79. Пирамида: проецирование: б чертеж в системе прямоугольных проекций; в изометрический проекции Фронтальная и профильная проекции пирамиды — равнобедренные треугольники. Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h. Изометрическую проекцию пирамиды начинают строить с основания. Из центра полученной фигуры проводят перпендикуляр, откладывают на нем высоту пирамиды и соединяют полученную точку с вершинами основания. Проецирование цилиндра и конуса. Если круги, лежащие и основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости H, их проекции на эту плоскость будут также кругами (рис. 80, б и д). Рис. 79. Пирамида: проецирование: б чертеж в системе прямоугольных проекций; в изометрический проекции Фронтальная и профильная проекции пирамиды — равнобедренные треугольники. Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h. Изометрическую проекцию пирамиды начинают строить с основания. Из центра полученной фигуры проводят перпендикуляр, откладывают на нем высоту пирамиды и соединяют полученную точку с вершинами основания. Проецирование цилиндра и конуса. Если круги, лежащие и основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости H, их проекции на эту плоскость будут также кругами (рис. 80, б и д).  Рис. 80. Цилиндр и конус: а, г — проецирование; б, д чертежи в системе прямоугольных проекций; в. е — изометрические проекции Фронтальная и профильная проекции цилиндра в этом случае прямоугольники, а конуса — равнобедренные треугольники. Заметьте, что на всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса. Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря значку "диаметр" можно представить форму цилиндра по одной проекции (рис. 81). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях. Рис. 80. Цилиндр и конус: а, г — проецирование; б, д чертежи в системе прямоугольных проекций; в. е — изометрические проекции Фронтальная и профильная проекции цилиндра в этом случае прямоугольники, а конуса — равнобедренные треугольники. Заметьте, что на всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса. Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря значку "диаметр" можно представить форму цилиндра по одной проекции (рис. 81). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях. 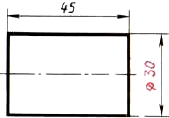 Рис. 81. Изображение цилиндра в одном виде Размеры цилиндра и конуса определяются их высотой h и диаметром основания d. Способы построения изометрической проекции цилиндра и конуса одинаковы. Для этого проводят оси х и у, на которых строят ромб. Стороны его равны диаметру основания цилиндра или конуса. В ромб вписывают овал (см. рис. 66). Проекции группы геометрических тел. На рисунке 83 даны проекции группы геометрических тел. Можете ли вы сказать, сколько геометрических тел входит в эту группу? Какие это тела? Рис. 81. Изображение цилиндра в одном виде Размеры цилиндра и конуса определяются их высотой h и диаметром основания d. Способы построения изометрической проекции цилиндра и конуса одинаковы. Для этого проводят оси х и у, на которых строят ромб. Стороны его равны диаметру основания цилиндра или конуса. В ромб вписывают овал (см. рис. 66). Проекции группы геометрических тел. На рисунке 83 даны проекции группы геометрических тел. Можете ли вы сказать, сколько геометрических тел входит в эту группу? Какие это тела? 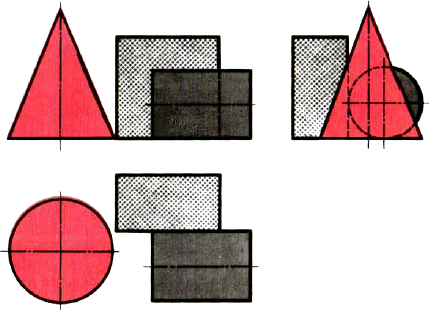 Рис. 83. Чертеж группы геометрических тел Рассмотрев изображения, можно установить, что на нем даны конус, цилиндр и прямоугольный параллелепипед. Они различно расположены относительно плоскостей проекций и друг друга. Как именно? Ось конуса перпендикулярна горизонтальной плоскости проекций, а ось цилиндра — профильной плоскости проекций. Две грани параллелепипеда параллельны горизонтальной плоскости проекций. На профильной проекции изображение цилиндра находится справа от изображения параллелепипеда, а на горизонтальной — ниже. Это значит, что цилиндр расположен впереди параллелепипеда, поэтому часть параллелепипеда на фронтальной проекции показана штриховой линией. По горизонтальной и профильной проекциям можно установить, что цилиндр касается параллелепипеда. Фронтальная проекция конуса касается проекции параллелепипеда. Однако, судя по горизонтальной проекции, параллелепипед не касается конуса. Конус расположен левее цилиндра и параллелепипеда. На профильной проекции он частично их закрывает. Поэтому невидимые участки цилиндра и параллелепипеда показаны штриховыми линиями. Как изменится профильная проекция на рисунке 83, если из группы геометрических тел удалить конус? Занимательные задачи 1. На столе лежат шашки, как показано на рисунке 84, а. Сосчитайте по чертежу, сколько шашек находится в первых ближних к вам столбиках. Сколько всего шашек лежит на столе? Если вы затрудняетесь сосчитать их по чертежу, попробуйте сначала сложить шашки в столбики, пользуясь чертежом. Теперь попробуйте правильно ответить на вопросы. Рис. 83. Чертеж группы геометрических тел Рассмотрев изображения, можно установить, что на нем даны конус, цилиндр и прямоугольный параллелепипед. Они различно расположены относительно плоскостей проекций и друг друга. Как именно? Ось конуса перпендикулярна горизонтальной плоскости проекций, а ось цилиндра — профильной плоскости проекций. Две грани параллелепипеда параллельны горизонтальной плоскости проекций. На профильной проекции изображение цилиндра находится справа от изображения параллелепипеда, а на горизонтальной — ниже. Это значит, что цилиндр расположен впереди параллелепипеда, поэтому часть параллелепипеда на фронтальной проекции показана штриховой линией. По горизонтальной и профильной проекциям можно установить, что цилиндр касается параллелепипеда. Фронтальная проекция конуса касается проекции параллелепипеда. Однако, судя по горизонтальной проекции, параллелепипед не касается конуса. Конус расположен левее цилиндра и параллелепипеда. На профильной проекции он частично их закрывает. Поэтому невидимые участки цилиндра и параллелепипеда показаны штриховыми линиями. Как изменится профильная проекция на рисунке 83, если из группы геометрических тел удалить конус? Занимательные задачи 1. На столе лежат шашки, как показано на рисунке 84, а. Сосчитайте по чертежу, сколько шашек находится в первых ближних к вам столбиках. Сколько всего шашек лежит на столе? Если вы затрудняетесь сосчитать их по чертежу, попробуйте сначала сложить шашки в столбики, пользуясь чертежом. Теперь попробуйте правильно ответить на вопросы. 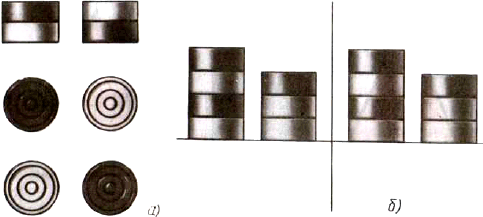 Рис. 84. Задания для упражнений 2. На столе в четыре столбика расположены шашки. На чертеже они показаны двумя проекциями (рис. 84, б). Сколько шашек на столе, если черных и белых поровну? Для решения этой задачи нужно не только знать правила проецирования, но и уметь логически рассуждать. Рис. 84. Задания для упражнений 2. На столе в четыре столбика расположены шашки. На чертеже они показаны двумя проекциями (рис. 84, б). Сколько шашек на столе, если черных и белых поровну? Для решения этой задачи нужно не только знать правила проецирования, но и уметь логически рассуждать. |
Графическая работа:
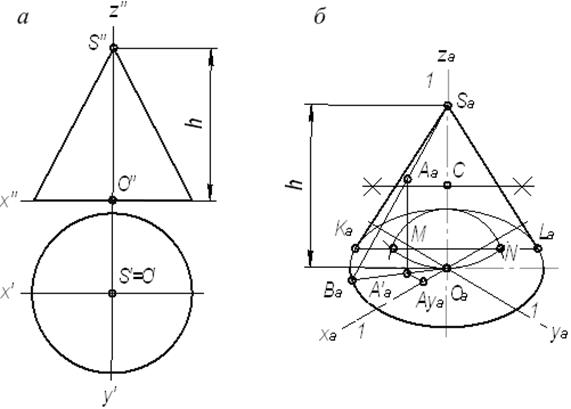
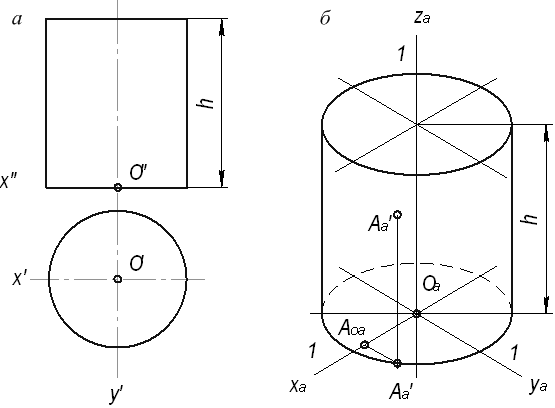
! Выполнить построение аксонометрических проекций геометрических тел с точками на поверхности по комплексным чертежам.
