Лекция №5. Математические предложения и методика изучения теорем
1.Виды математических предложений
2.Логическая структура теорем. Виды теорем и связь между ними
3.Необходимые и достаточные условия, теоремы – свойства и теоремы – признаки
4.Методика обучения доказательству
I.Каждая математическая теория представляет собой множество предложений, описывающих структуру этой теории. С каждым математическим предложением связаны содержание (выраженное в нем математическое содержание) и логическая форма (или структура). В математике различают элементарные и составные предложения. Составные предложения образуются из элементарных с помощью логических связок “не”, “и”, “или”, “если …, то”, “тогда и только тогда”, “для всякого”, обозначающих логические операции.
Выявить логическую структуру составного предложения – значит установить:
1) Из каких элементарных предложений образовано данное составное предложение;
2) С помощью каких логических связано.
а)“ 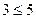 ” б) “
” б) “ 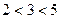 ”
”
Это сложное предложение:
а) 1) 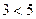 2)
2) 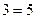 а) 1)
а) 1) 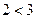 2)
2) 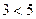
б) или (дизъюнкция) б) и (конъюнкция)
К математическим предложениям относятся:
· Теорема – математическое предложение, истинность которого доказывается,
· Аксиома– математическое предложение, истинность которого принимается без доказательства,
· Определения математических понятий.
Среди суждений, устанавливающих различные отношения между математическими понятиями, выделяют высказывания и высказывательные формы.
Определение. Высказываниемназывается предложение, относительно которого имеет смысл вопрос, истинно оно или ложно.
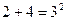 - ложное высказывание.
- ложное высказывание.
Определение. Высказывательная форма – это предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке в него конкретных значений переменных.
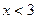 - одноместная высказывательная форма
- одноместная высказывательная форма
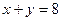 - двуместная высказывательная форма
- двуместная высказывательная форма
II.Каждая теорема состоит из 3 частей:
· разъяснительная часть
· условие
· заключение
В разъяснительной части описывается, какие точки или фигуры рассматриваются в теореме. Для словесного выражения теорем обычно используют две формы суждений: категоричную, условную (импликативную).
Категоричная – когда принадлежность или непринадлежность некоторого признака предмету независимо от каких бы то ни было условий.
Условная – когда истинность суждения ставится в зависимости от определенных условий.
Если теорема содержит несколько условий и заключений, то теорема сложная.
Логико – математический анализ теоремы предполагает:
1) установление формы суждения;
2) выделение разъяснительной части, условия, заключений;
3) установление факта, какая дана теорема – простая или сложная.
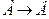 - прямая теорема
- прямая теорема
Если разъяснительную часть оставить без изменения, а условие и заключение поменять местами, то получим утверждение обратное данному. ( 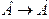 )
)
Если разъяснительную часть оставить без изменения, а условие и заключение утверждения заменить их отрицанием, то получим утверждение противоположное данному. 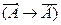
Если оставить без изменения разъяснительную часть и поменять местами условие и заключение утверждения, противоположного данному, то получим утверждение, обратное противоположному. 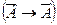


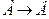
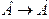
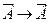
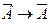
Утверждения 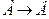 ,
, 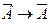 всегда одновременно истинны или ложны. Эта связь между теоремами используется при доказательстве методом от противного. Если первую теорему трудно доказать, то её заменяем на обратную противоположной.
всегда одновременно истинны или ложны. Эта связь между теоремами используется при доказательстве методом от противного. Если первую теорему трудно доказать, то её заменяем на обратную противоположной.
Схема метода доказательства от противного:
1) предлагаем противоположное тому, что требуется доказать, т.е. …
2) из предложения следует, что …
3) получаем противоречие с …
4) значит наше предположение неверно, а верно то, что требовалось доказать, т.е …
III.Если из предложения 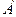 следует предложение
следует предложение 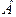 , то говорят, что
, то говорят, что 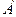 - достаточное условие для
- достаточное условие для 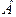 , а
, а 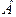 - необходимое условие для
- необходимое условие для 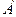 .
.
Другими словами, предложение 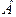 называется необходимым условием для
называется необходимым условием для 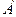 , если оно логически следует из
, если оно логически следует из 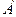 . Предложение
. Предложение 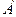 называется достаточным условием для
называется достаточным условием для 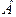 ,если
,если 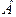 из него следует.
из него следует.
Если 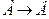 “и”,
“и”, 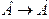 “и”, то говорят, что
“и”, то говорят, что 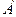 является необходимым и достаточным условием для
является необходимым и достаточным условием для 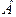 , и наоборот.
, и наоборот.
 Пример: Если число делится на 10, то оно делится на 2.
Пример: Если число делится на 10, то оно делится на 2.
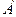
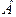
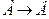 истинно, т.е.
истинно, т.е. 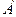 - достаточное для
- достаточное для 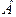 ,
,
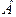 - необходимое для
- необходимое для 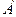 .
.
Определение. Под свойствомпонимается обязательное условие принадлежности объекта к данному виду.
Другими словами, свойство – это то, что мы можем получить (или доказать), исходя из того, что объект принадлежит к данному виду.
Например, мы знаем, что 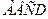 - ромб. Следовательно, мы можем утверждать, что:
- ромб. Следовательно, мы можем утверждать, что:
¾ 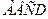 - четырехугольник
- четырехугольник
¾ 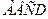 - параллелограмм
- параллелограмм
¾ диагонали 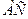 и
и 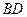 перпендикулярны
перпендикулярны
и т.д.
Все это – свойства ромба. Иначе их называют необходимымиусловиями того, что 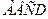 - ромб.
- ромб.
Свойство для любого понятия можно сформулировать по следующей схеме:
Если что-то является объектом такого-то вида,
то
для него выполняется то-то.
Признак –это достаточное условие, т.е. такое, которое формулируется по схеме:
Если для данного объекта выполняется такое-то условие,
то
объект принадлежит к рассматриваемому виду.
В математике часты случаи, когда одно и то же условие является и свойством, и признаком данного понятия.
Пример.
Признак: Если в четырёхугольнике диагонали пересекаются в одной точке и делятся ею пополам, то четырёхугольник является параллелограммом.
Свойство: Если четырёхугольник является параллелограммом, то его диагонали пересекаются в одной точке и делятся ею пополам.
Такое условие, которое является одновременно и признаком, и свойством, называется характеристическим свойством понятия. Сформулировать можно его двумя способами с использованием слов: или “необходимо и достаточно”, или “тогда и только тогда”.
Пример.
1) Четырехугольник является параллелограммом тогда и только тогда, когда его диагонали пересекаются в одной точке и делятся ею пополам.
2) Для того чтобы четырехугольник являлся параллелограммом необходимо и достаточно, чтобы его диагонали пересекались и делились ею пополам.
IV.При изучении теоремы можно условно выделить следующие этапы:
1) подготовительный этап
2) введение
3) усвоение
4) закрепление
I. Осуществляется актуализация знаний, необходимых для введения и доказательства теоремы.
¾ мотивация изучения теоремы:
a) обобщение необходимых в жизни фактов и явлений и перевод их на математический язык;
b) показать необходимость знания той или иной теоремы для решения практических задач;
c) показать, как решалась данная проблема в истории науки.
¾ с помощью практической работы подвести к открытию теоремы.
II.
¾ разобраться в структуре теоремы (дано, доказать);
¾ сделать чертеж и краткую запись
¾ поиск доказательства: он может осуществляться с помощью различных приемов. например, конструирование идеи доказательства, исходя из требования теоремы; обращение к известным методам доказательтва4 использование идеи рассматривать взаимное расположение данных и появившихся в ходе доказательства фигур и т .д. Завершается поиск составлением плана доказательства.
¾ оформление доказательства
III.С помощью специально подобранных заданий и вопросов осуществить:
¾ Усвоение формулировки
¾ Усвоение доказательства
¾ Решение простейших задач (по готовому чертежу) на непосредственное применение теоремы.
IV. Решение разнообразных задач, повторение доказательства.
Замечания.
1.При поиске путей доказательства следует иметь ввиду:
1) Если в доказательстве используется известный учащимся метод или доказательство осуществляется по известной уже схеме, то учащимся сообщается метод, а дальше беседа по плану:
¾ каков 1-ый шаг данного метода?
¾ Как это сделать для данной теоремы?
¾ …
2) если теорема содержит небольшое число этапов доказательства, каждый из которых “прозрачно” связан с другим, то применяем аналогичные рассуждения: что нужно знать, чтобы доказать (с конца)
3) если теорема сложная, то ученикам следует сообщить идею доказательства.
2.На этапе усвоения доказательства задаем вопросы:
¾ Какова схема доказательства?
¾ Каковы этапы доказательства?
¾ На чем основывается каждый этап?
