Алгоритмизация линейного, разветвляющегося и

ЦИКЛИЧЕСКОГО ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА

Цель работы:выработать практические навыки в построении блок-схем на линейный, разветвляющийся и циклический вычислительные процессы.

Общие сведения

1 Линейный вычислительный процесс

Алгоритм линейной структуры - алгоритм, в котором блоки выполняются друг за другом. Такой порядок выполнения блоков называется естественным. При этом не могут использоваться операции перехода и условные операции.

Пример 1. Вычислить y = 2cos²x, где x=2lna; a=6,7.

Порядок работы

Шаг 1. Вводим a.

Шаг 2. Вычисляем x = 2lna.

Шаг 3. Вычисляем y = 2cos²x.

Шаг 4. Печатаем y.

Шаг 5. Останов.

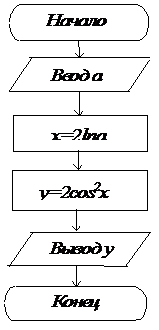Блок-схема

2 Разветвляющийся вычислительный процесс

Алгоритм разветвляющейся структуры - алгоритм, в котором предусмотрено разветвление выполняемой последовательности действий в зависимости от результата проверки какого-либо условия.

Пример 2. Вычислить корни квадратного уравнения

ax² + bx + c = 0

при условии

d = b²-4ac ³ 0

по формуле

.

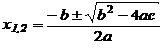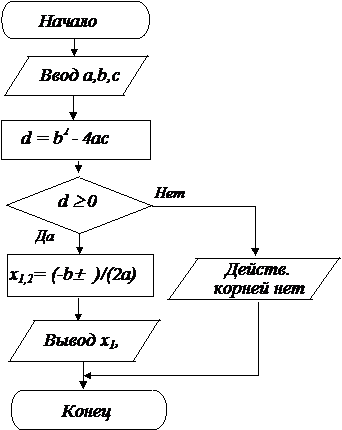В противном случае, т.е. при d<0, предусмотреть вывод сообщения «Действительных корней нет».

Блок-схема

Порядок работы

Шаг 1. Вводим a, b, c.

Шаг 2. Вычисляем d = b² - 4ac.

Шаг 3. Если d<0, выводим сообщение «Действительных корней нет», останов.

Шаг 4. Вычисляем

.

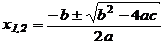Шаг 5. Выводим x₁, x₂.

Шаг 6. Останов.

3 Циклический вычислительный процесс

Алгоритм циклической структуры - алгоритм, в котором предусмотрено неоднократное выполнение одной и той же последовательности действий, называемой циклом.

Структура цикла: вначале устанавливаем начальные значения всем переменным цикла, т.е. определяем их состояние до первого выполнения операций. Затем описываем операции, выполняемые многократно, т.е. тело цикла, далее изменяем переменную, определяющую количество повторов цикла, т.е. параметр цикла. Завершается алгоритм условием выхода из цикла.

Пример 3. Вычислить y = sin(3x)/x при 1 £ x £ 100 с шагом 0,5.

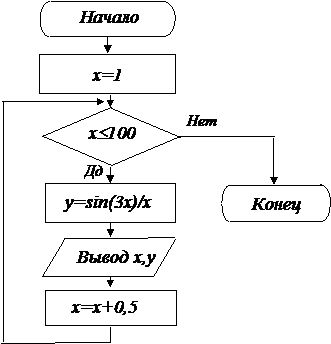Блок-схема

Порядок работы

Шаг 1. Задаем начальное значение x=1.

Шаг 2. Пока x £ 100, выполняем шаги 3-6, иначе - шаг 7.

Шаг 3. Вычисляем y = sin(3x)/x.

Шаг 4. Выводим x, y.

Шаг 5. Увеличиваем значение x на шаг: x = x + 0,5.

Шаг 6. Возвращаемся на шаг 2.

Шаг 7. Останов.

Пример 4. Найти сумму ряда

y = 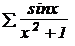, при 0 £ x £ p , D x = p /20.

Порядок работы

Шаг 1. Установим начальное значение суммы s = 0.

Шаг 2. Определим начальное значение параметра цикла x = 0.

Шаг 3. Пока x £ p , выполняем шаги 3-7, иначе - идем на шаг 8.

Шаг 4. Вычисляем y = sinx / (x²+1).

Шаг 5. Вычисляем сумму s = s + y.

Шаг 6. Увеличиваем значение x на шаг: x = x + p /20.

Шаг 7. Возвращаемся на шаг 3.

Шаг 8. Останов.

Задания для самостоятельной работы

Задание 1. Нарисовать блок-схему для вычисления h, взяв значения функций из таблицы 2.

Таблица 2

Вар.	h	a	b	с	x
	a2+b2-6c	x2-e-x	lnx+	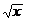cos2x+x5	5,4
	c2+8b+10a	sin2x+x1/4	tgx-8x3	x4+2sinx2	1,2
	3a2+4b-8	3x-2cos3x	lnx+2ex	x1/3+4x-1	0,3
	a3+b2-8c	sin3x+x4	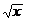-lnx	4x-5x3	1,7
	6b3+4c-2	tgx+e2x	x2-6x3	1/x-2lnx	4,1
	a2+b2+c2	ex+e2x+4	x-sin3x	x2/cos3x	2,4
	5b3-2a+c	tgx-2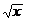x	-sinx	x3/7	5,5
	4a2+5b2	cosx+2x	x4-2x/5	2x-5	4,6
	3ab-4c	sin2x+5	cosx5	x1/3+tgx	1,6
	c2+5a3-b	cos3x-6x	-4x3+lnx	e2x+4cosx	4,6
	2a+4c-b4	ex-2lnx	2x-5/x	x5-2lnx	3,9
	a2+b2+c2	2/x+x3	lnx2-4x	tgx-sin2x	4,1
	(a+b)2	lnx+2ex	tgx+e2x	x2-e-x	3,4
	2ac-3cb	1/x-2lnx	cosx+2x	sin2x+x1/4	1,9
	5c+2a4	x2-2/x	(2-x)/6	cos3x-2x	2,3
	a+b+c	lnx/2x	x3-4x	tgx-2x	4,2
	2a+3b+4c	x2+x3	lnx-x4	cos2(x-4)	2,8
	a2+b3+c4	sin2x+x1/4	x3+4x	ex+2lnx	1,3
	a+2b+3c	2x-x1/4	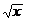-2cosx	tgx-4x	3,1
	2(a+b)-c4	(x3-x/2)3	lnx-e2x		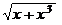2,4
	c2-b3	2x+sinx4	sin(x-lnx)	lnx2+2x	1,1
	3a-4cb	2cosx3	tgx/4	x/5	3,1
	c5-2ab	1/2sin3x	sin6x/x3	x-4sin2x	1,8
	6a+3b3+c	cosxx+2x	sin2x+tgx	lnx-e-x	2,1
	4abc	xx-sinx3	x/2-x5	2x-sin3x	4,1
	a2+(b-c)5/3	2x1/3+1	sin(x2+4)	lncos3x	5,3
	(a+4b)1/3-c2	tg(2x)/4	cosx2/x1/5	e-2x+1/x2	3,8
	a1/3+(b3-c)	x+23x	lnsin34x	arcsin2x	4,2
	b3+(a-4c)1/5	53x/(3x-1)	e-5x+4/x	cos(x1/3)	2,6
	c1/5-(b+3a)2	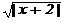+ex	cosx+x2	arctg(x3)	1,3

Задание 2. Нарисовать блок-схему для вычисления

y = f(x), где

ì f₁(z), если z < 0;

x = í f₂(z), если 0 £ z £ 8;

î f₃(z), если z > 8;

z = cos(с).

Значения функций приведены в таблице 3.

Таблица 3

Вар.	f(x)	f1(z)	f2(z)	f3(z)	c
	x2+8x-6	z3-3z2	zln(z)	ez-e-z	5,1
	x3lnx2	e-z+3z	ln|z|	cosz+z2	5,4
	x1/4+sinx	2z-ln|z|	tgz-2z	sin3z	4,1
	x4+2sinx2	sinz+tgz	cos3z+3/z	z2+lnz2	3,2
	cosx3	z2+2sinz	lnz+2z	ez+1/z	4,7
	sinx+2lnx	2z+tgz	lnz4+2z	cosz+2z	1,3
	sin4x2	sinz2-z3		2sinz2	1,6
	tgx-4x3	1/cos2z	z-ln|z|	z3+sinz	1,5
	lnx-e2x	z2+ez	cos4z/z3	tg(z+1/z)	2,7
	2x-lnx	2cosz+1/z	z3-2ln|z|	tg2z+z3	3,8
	3x-sinx	3tg3z	1/cos4z	e2z+sinz	1,6
	4x2+cosx	3z/sinz	z2+2sinz	2z-ln|z|	2,4
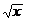	+cosx	z2+lnz2	ez+1/z	z4-sinz	4,1
	x1/3+2x	ln|cosz|	2z+ez	tg2z	2,5
	sin4x+2x	z5/sin2z	e-2z+tgz	cos4z+z1/3	3,2
	tg4x+1/x	z/sinz1/5	2ztg3z	z 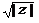+8	1,4
	ln(1/x)	zsin2z-8	lnsinz0,8	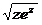-2,5	2,3
	e2x+4x	cos(p /4)-z	1/(ez+1)	arctg(z+3)	4,1
	cosx4+x/2	sin(z+30° )	lncos(pz/6)	e-tg(z-2)	3,2
	2tgx+ex	z+cos(p +z)	z3+z1/3	z4-lnz	2,8
	2lnx2	arccosz2	sinz+lncosz	z3-sin(p x)	1,7
	cos2x/3	z2+ln(z+4)	e(z-5)+sinz		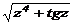2,2
	1/tgx4	e-4z+2+z2	cos(z1/3+2)	sin(p +4z2)	5,6
	e2x-x3	tg(z2+ 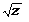)	ln(sinz+5)	z4+z2-cosz	3,4
	tgx-2lnx	arcsin(z+3)	z3-z2+cosz	ln(z3+4z)	2,5
	cosx4+x/2	lnsinz0,8	cos(p /4)-z	z/sinz1/5	3,7
	ln(x+x2)	2ztg3z	sin(p +4z2)	z3+z1/3	2,6
	cosx4+2x	tg(z+1/z)	e2z+sinz	cosz1/5	3,8
	sin4x+2x	z2+lnz2	cos3z+3/z	cos(p /4)-z	5,8
	3ln(x2+5)	z4-lnz	sinz+tgz	sinz+lncosz	3,5

Задание 3. Найти сумму ряда

y = 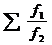, где a £ x £ b, D x = c.

Варианты заданий приведены в таблице 4.

Таблица 4

Вар.	f1	f2	a	b	c
	3x-1	e-1/x+x/(x+1)			0,5
	x3-3x2	x4+2x2+3			0,2
	e-x+4x		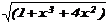0,6	4,2	0,3
	sin2(x+4x3)	(x+2x3)	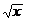0,5	4,8	0,2
	xsinx3-ln2x	arctgx/4+e-x+2		6,3	0,4
	x4-cosx	tgx+2x			0,5
	2x+sin2x		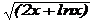		0,3
	ln(4x+8)	e-x+sin2x			0,2
	x3ln(2x)	4x2+6x3-2	0,5		0,3
	x2+sin3x	cos3x+e-2x	-2		0,4
	xe-x	sin4x+x3	1,5		0,3
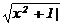		arctgx/5+2x	0,6		0,2
	x2/(3x+2)	sin2(p x+1)	0,5	5,2	0,3
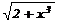		3x/(x-2)	1,2	6,3	0,4
	x3x+1+8x	|x-8|+sinx		7,5	0,3
	x4+ex+3	xarctg(x/3)		6,4	0,2
	ln2(x+4)	sin3(x/5)		6,8	0,3
	ex-2+x3	x-ln|x-1|			0,4
	2cos(x+3)	4x2/(3+x3)			0,3
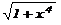	)	tg2(x+4)-e-x			0,4
	3+2sin2(x-3)	4+x/10			0,5
	ln(1(1+2x)	sin2(4x+1)	1,5	6,8	0,4
	+e-x	5arctg(4x)			0,5
	arcsin(x+2)	3(x-4)/(x2+1)			0,2
	e|x+2|	ln2(x+4)	-2		0,3
	(4-x)cos2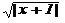x	+e-3x			0,4
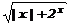		sinx4-4	-2		0,2
	2x+4+cos2x	ln|x+8|	-4		0,5
	(x+2)/sin3x		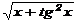		0,3
	ex+3+4x2	arcsinx3			0,2

Лабораторная работа 2