Бесконечно малые и бесконечно большие функции.
Бесконечно малые и бесконечно большие функции.
Опр. Функция y =  (x) наз. бесконечно малойпри х
(x) наз. бесконечно малойпри х  а , если lim
а , если lim  (x) = 0. Функция y = f(x) наз. бесконечно большойпри х
(x) = 0. Функция y = f(x) наз. бесконечно большойпри х  а ( lim f(x) =
а ( lim f(x) = 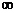 ) , если становится больше любого наперед заданного числа , или, если для любого числа М > 0 существует такое число
) , если становится больше любого наперед заданного числа , или, если для любого числа М > 0 существует такое число 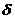 , зависящее только от М , что из неравенства0 < |x – a| <
, зависящее только от М , что из неравенства0 < |x – a| < 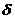 следует неравенство |f(x)| > M
следует неравенство |f(x)| > M
Теорема. Функция обратная к бесконечно малой является бесконечно большой и наоборот.
Действительно, если бесконечно малая функция  (х)при х
(х)при х  а оказывается в знаменателе дроби, то дробь неограниченно возрастает и становится бесконечно большой функцией 1/
а оказывается в знаменателе дроби, то дробь неограниченно возрастает и становится бесконечно большой функцией 1/  (х) при х
(х) при х  а.
а.
Леммы о бесконечно малых.
Лемма 1. Алгебраическая сумма конечного числа бесконечно малых при х  а является бесконечно малой.
а является бесконечно малой.
Док-во. Пусть U(x) =  (x) +
(x) + 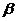 (x) , где lim
(x) , где lim  (x) = 0 , lim
(x) = 0 , lim 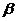 (x) = 0 при х
(x) = 0 при х  а.
а.
Возьмем произвольное число 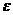 > 0. Поскольку функции
> 0. Поскольку функции  (х) и
(х) и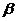 (х) имеют предел, то всегда можно подобрать такой интервал |х – 0| <
(х) имеют предел, то всегда можно подобрать такой интервал |х – 0| < 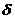 , что |
, что | (x) – 0| <
(x) – 0| < 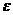 /2, |
/2, | 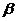 (x) – 0| <
(x) – 0| < 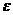 /2 и, следовательно, |
/2 и, следовательно, |  (х) +
(х) + 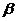 (х) - 0| <
(х) - 0| < 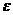 . Последнее неравенство означает, что разность |U(x) – 0| делается меньше любого
. Последнее неравенство означает, что разность |U(x) – 0| делается меньше любого 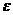 , лишь только |х – а| становится меньше соответствующего
, лишь только |х – а| становится меньше соответствующего 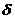 , т.е. функция U(x) имеет предел в точке 0 : lim U(x) = 0 при х
, т.е. функция U(x) имеет предел в точке 0 : lim U(x) = 0 при х  а .
а .
Опр. Функция y = f(x) наз. ограниченной в окрестности точки а, если существует число М> 0, такое что |f(x)| < M в этой окрестности.
Всякая функция y = f(x), имеющая предел lim f(x) = b при х  а ограничена в окрестности точки а . Действительно, |f(x)| = |f(x) – b + b| < |f(x) – b| + |b| <
а ограничена в окрестности точки а . Действительно, |f(x)| = |f(x) – b + b| < |f(x) – b| + |b| <  (x) + |b|
(x) + |b|
Лемма 2. Произведение ограниченной в окрестности точки а функции на бесконечно малую при х  а является бесконечно малой.
а является бесконечно малой.
Док-во. Пусть 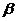 (x) = f(x)
(x) = f(x)  (x) , где |f(x)| < M и lim
(x) , где |f(x)| < M и lim  (x) = 0 при х
(x) = 0 при х  а
а
Т.к. функция  (х) имеет предел в точке 0 , то для любого числа
(х) имеет предел в точке 0 , то для любого числа 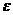 /М>0 найдется
/М>0 найдется
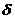 - окрестность точки а, в которой |
- окрестность точки а, в которой |  (х) – 0 | <
(х) – 0 | < 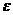 /M и, следовательно, интервал |
/M и, следовательно, интервал | 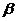 (х) - 0 | = |f(x)| |
(х) - 0 | = |f(x)| |  (x) – 0 | < M
(x) – 0 | < M 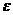 /M =
/M = 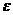 будет уже произвольной величины
будет уже произвольной величины 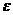 , что означает lim
, что означает lim 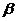 (x) = 0 при х
(x) = 0 при х  а , т.е. произведение f(x)
а , т.е. произведение f(x)  (х) есть б.м.в. в окрестности точки а .
(х) есть б.м.в. в окрестности точки а .
Теоремы о пределах.
Вычисление пределов функций основывается на следующих теоремах:
Сравнение бесконечно малых.
Пусть при x®aфункции a(х) и b(х) - бесконечно малые. Тогда :
1.Если 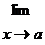
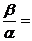 0 , то b наз. бесконечно малой высшего порядка относительно a.
0 , то b наз. бесконечно малой высшего порядка относительно a.
2. Если 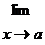
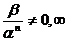 , то b наз. бесконечно малой n – ого порядка относительно a.
, то b наз. бесконечно малой n – ого порядка относительно a.
3. Если 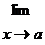
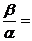 1 , то a и b наз. эквивалентными бесконечно малыми. a » b
1 , то a и b наз. эквивалентными бесконечно малыми. a » b
При вычислении пределов эквивалентные бесконечно малые могут заменять друг друга.
Замечательные пределы.
Теперь имеем два способа определения значения функции в точке: а) прямая подстановка аргумента в формулу y = f(x) ; б) предельный процесс - процесс осторожного приближения к выбранной точке. В большинстве случаев оба способа дают одинаковый результат, но в отдельных точках прямая подстановка приводит к неопределенностям типа {0/0}, {¥/¥}, {¥ - ¥}, { 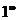 }, {
}, { 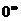 }, {
}, { 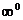 }.Тогда значение функции определяется через предельный процесс и процедуру раскрытия неопределенностей.
}.Тогда значение функции определяется через предельный процесс и процедуру раскрытия неопределенностей.
В основе аппарата мат.анализа лежат пределы нескольких функций, которые получили название - замечательные пределы. Раскроем их неопределенности.
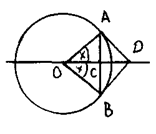
Первый замечательный предел lim sinx / x = 1 при x® 0
Имеем окружность R = 1 и касательные AD, BD. Из прямоугольных DОАС и DОАD следует: sin x = AC/1, tg x = AD/1. Точки А и В соединяют три линии: прямая АВ = 2АС = 2 sin x, дуга АВ = 2х и ломаная ADB = 2 AD = 2 tg x. Из соотношения длин этих линий следует: 2sin x < 2x < 2tg x Þ 1 < x/sin x < 1/cos x Þ Þ 1 > sin x / x > cos x . При переходе в неравенстве к пределу x ® 0 имеем lim cos x = 1, 1 ³ lim sin x / x ³ 1 и, следовательно, lim sin x / x =1 при x ® 0.
Натуральное число e.
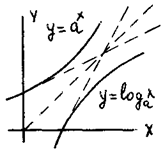 Логарифмическая функция y = logaxявляется обратной для показательной функции y = ax .Графики этих функций расположены симметрично относительно биссектрисы y = x и при произвольном а пересекают оси Ох, Оу всегда в одной точке (1;0 ) и (0;1). Проведем через эти точки касательные к кривым. Они пересекуться на биссектрисе и точка пересечения будет перемещаться вдоль нее при изменении основания а . В определенный момент, при а = 2,72 . . . касательные станут
Логарифмическая функция y = logaxявляется обратной для показательной функции y = ax .Графики этих функций расположены симметрично относительно биссектрисы y = x и при произвольном а пересекают оси Ох, Оу всегда в одной точке (1;0 ) и (0;1). Проведем через эти точки касательные к кривым. Они пересекуться на биссектрисе и точка пересечения будет перемещаться вдоль нее при изменении основания а . В определенный момент, при а = 2,72 . . . касательные станут
параллельны друг другу и оси симметрии. Их угловой коэффициент k = tg 450 = 1 . Основание логарифма, приводящее к высшей степени симметрии графиков показательной и логарифмической функций, наз. натуральным числом и обозначается е = 2,72 . . . . Многие соотношения связанные с е удивительно просты и симметричны.
Непрерывность функции.
 С понятием предела функции связано другое важное понятие – непрерывность функции.На графике непрерывным функциям соответствуют непрерывные линии.
С понятием предела функции связано другое важное понятие – непрерывность функции.На графике непрерывным функциям соответствуют непрерывные линии.
Пусть y = f(x) определена в точке хo и ее окрестности. Величина  х = х – хoназ. приращением аргумента,
х = х – хoназ. приращением аргумента,  y = y – yo- соответствующим приращением функции.
y = y – yo- соответствующим приращением функции.
Опр.1Функция y = f(x)наз. непрерывнойв точке х, если она определена в этой точке и ее окрестности и бесконечно малому приращению аргумента  хсоответствует бесконечно малое приращение функции
хсоответствует бесконечно малое приращение функции  y, т.е.
y, т.е.
lim  y = 0при
y = 0при  х
х  0( 1 )
0( 1 )
Следствие:Основные элементарные функции являются непрерывными во всех точках области определения D(f), т.к. они имеют предел в каждой из точек и удовлетворяют условию ( 1 )
y = ax ,  y =
y = 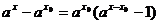 , lim
, lim  y =
y = 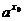 lim (a
lim (a 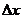 - 1) = 0при
- 1) = 0при  х
х  0
0
y = loga x ,  y = loga(x +
y = loga(x +  x) - loga x = loga (1 +
x) - loga x = loga (1 +  x/x), lim
x/x), lim  y = lim loga(1 +
y = lim loga(1 +  x/x) = 0
x/x) = 0
y = x2 ,  y = (x +
y = (x +  x)2 - x2 = 2x
x)2 - x2 = 2x  x + (
x + (  x)2 , lim
x)2 , lim  y = lim [2x
y = lim [2x  x + (
x + (  x)2 ] = 0
x)2 ] = 0
Опр.2Функция y = f(x)наз. непрерывной в точке хo ,если ее предел в хoсовпадает со значением функции в этой точке.
lim f(x) = f(xo)при x  xo( 2 )
xo( 2 )
Покажем эквивалентность этих определений:
lim  y = 0
y = 0 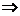 lim(f(x) – f(xo)) = 0
lim(f(x) – f(xo)) = 0 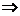 lim f(x) = f(xo), при
lim f(x) = f(xo), при
 x
x  0 x
0 x  xo const x
xo const x  xo
xo
Условие ( 2 ) позволяет для непрерывных функций переход к пределу функции заменить на переход к пределу аргумента
lim f(x) = f (lim x ) , при( 3 )x  xo x
xo x  xo
xo
Для y = f(x) определенной на [a,b]предельный процесс около внутренней точки x(a < x < b)можно организовать двумяспособами, подходя к точке xслева или справа lim f(x) = f(xo – 0) , lim f(x) = f(xo + 0)
x  xo - 0 x
xo - 0 x  xo + 0
xo + 0
Это левосторонний и правосторонний пределы.
Опр.3Функция y = f(x)наз. непрерывной в точке хo ,если ее левосторонний и правосторонний пределы совпадаютf(xo – 0) = f(xo+ 0) = f(xo)
Опр.Функция y = f(x)наз. непрерывной на промежутке [a,b] , если она непрерывна в каждой его точке. На концах lim f(x) = f(a) , lim f(x) = f(b)
x  a + 0 x
a + 0 x  b - 0
b - 0
Точки разрыва.
Непрерывность функции может быть нарушена в отдельных точках. Три типа точек разрыва :
1) x0 - устранимая точка разрыва, когда f(x0 - 0) = f(x0 + 0),но в самой точке х0функция не определена;
2) x0 - точка разрыва 1 рода, когда f(x - 0) 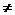 f(x + 0), но пределы конечны;
f(x + 0), но пределы конечны;
3) x0 - точка разрыва 2 рода, когда f(x - 0) 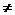 f(x + 0) и пределы бесконечны;
f(x + 0) и пределы бесконечны;
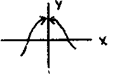

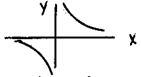
Пр.
y = sinx/ x, x = 0 f(x) = |x| /x, x = 0 y = 1/x, x = 0
Свойства функций, непрерывных в точке .
1)Если функции g(x) и h(x) непрерывны в точке хo, то функции g(x) + h(x),
g(x) h(x), g(x)/h(x)при h(xo) 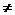 0также являются непрерывными функциями.
0также являются непрерывными функциями.
lim ( g(x) + h(x) ) = lim g(x) + lim h(x) = g(xo) + h(xo)
x  xo x
xo x  xo x
xo x  xo
xo
Для остальных функций доказательство аналогично.
2)Сложная функция, составленная из непрерывных функций, также является непрерывной.
Док-во. Пусть функция y = g(z)непрерывна в точке zo ,а z = h(x)в точке хo ,причем, zo = h(xo).По определению непрерывности lim h(x) = zo , lim g(z) = g(zo)
x – xo z – zo
Т.к. предел сложной функциипри х  хoравен значению функции в точке хo
хoравен значению функции в точке хo
lim g( h(x) ) = lim g(z) = g(zo) = g (h(xo) )
то функция является непрерывной .
Следствие.Элементарные функции образуются из основных элементарных функций с помощью арифметических операций или являются их суперпозициями. Поскольку основные элементарные функции непрерывны, то в силу свойств 1) и 2) все составленные из них элементарные функции также непрерывны и изображаются на графиках сплошными линиями в области своего определения.
Бесконечно малые и бесконечно большие функции.
Опр. Функция y =  (x) наз. бесконечно малойпри х
(x) наз. бесконечно малойпри х  а , если lim
а , если lim  (x) = 0. Функция y = f(x) наз. бесконечно большойпри х
(x) = 0. Функция y = f(x) наз. бесконечно большойпри х  а ( lim f(x) =
а ( lim f(x) = 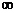 ) , если становится больше любого наперед заданного числа , или, если для любого числа М > 0 существует такое число
) , если становится больше любого наперед заданного числа , или, если для любого числа М > 0 существует такое число 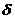 , зависящее только от М , что из неравенства0 < |x – a| <
, зависящее только от М , что из неравенства0 < |x – a| < 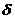 следует неравенство |f(x)| > M
следует неравенство |f(x)| > M
Теорема. Функция обратная к бесконечно малой является бесконечно большой и наоборот.
Действительно, если бесконечно малая функция  (х)при х
(х)при х  а оказывается в знаменателе дроби, то дробь неограниченно возрастает и становится бесконечно большой функцией 1/
а оказывается в знаменателе дроби, то дробь неограниченно возрастает и становится бесконечно большой функцией 1/  (х) при х
(х) при х  а.
а.
Леммы о бесконечно малых.
Лемма 1. Алгебраическая сумма конечного числа бесконечно малых при х  а является бесконечно малой.
а является бесконечно малой.
Док-во. Пусть U(x) =  (x) +
(x) + 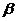 (x) , где lim
(x) , где lim  (x) = 0 , lim
(x) = 0 , lim 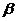 (x) = 0 при х
(x) = 0 при х  а.
а.
Возьмем произвольное число 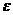 > 0. Поскольку функции
> 0. Поскольку функции  (х) и
(х) и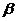 (х) имеют предел, то всегда можно подобрать такой интервал |х – 0| <
(х) имеют предел, то всегда можно подобрать такой интервал |х – 0| < 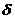 , что |
, что | (x) – 0| <
(x) – 0| < 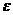 /2, |
/2, | 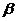 (x) – 0| <
(x) – 0| < 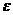 /2 и, следовательно, |
/2 и, следовательно, |  (х) +
(х) + 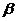 (х) - 0| <
(х) - 0| < 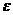 . Последнее неравенство означает, что разность |U(x) – 0| делается меньше любого
. Последнее неравенство означает, что разность |U(x) – 0| делается меньше любого 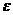 , лишь только |х – а| становится меньше соответствующего
, лишь только |х – а| становится меньше соответствующего 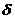 , т.е. функция U(x) имеет предел в точке 0 : lim U(x) = 0 при х
, т.е. функция U(x) имеет предел в точке 0 : lim U(x) = 0 при х  а .
а .
Опр. Функция y = f(x) наз. ограниченной в окрестности точки а, если существует число М> 0, такое что |f(x)| < M в этой окрестности.
Всякая функция y = f(x), имеющая предел lim f(x) = b при х  а ограничена в окрестности точки а . Действительно, |f(x)| = |f(x) – b + b| < |f(x) – b| + |b| <
а ограничена в окрестности точки а . Действительно, |f(x)| = |f(x) – b + b| < |f(x) – b| + |b| <  (x) + |b|
(x) + |b|
Лемма 2. Произведение ограниченной в окрестности точки а функции на бесконечно малую при х  а является бесконечно малой.
а является бесконечно малой.
Док-во. Пусть 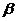 (x) = f(x)
(x) = f(x)  (x) , где |f(x)| < M и lim
(x) , где |f(x)| < M и lim  (x) = 0 при х
(x) = 0 при х  а
а
Т.к. функция  (х) имеет предел в точке 0 , то для любого числа
(х) имеет предел в точке 0 , то для любого числа 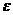 /М>0 найдется
/М>0 найдется
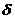 - окрестность точки а, в которой |
- окрестность точки а, в которой |  (х) – 0 | <
(х) – 0 | < 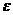 /M и, следовательно, интервал |
/M и, следовательно, интервал | 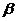 (х) - 0 | = |f(x)| |
(х) - 0 | = |f(x)| |  (x) – 0 | < M
(x) – 0 | < M 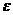 /M =
/M = 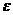 будет уже произвольной величины
будет уже произвольной величины 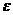 , что означает lim
, что означает lim 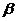 (x) = 0 при х
(x) = 0 при х  а , т.е. произведение f(x)
а , т.е. произведение f(x)  (х) есть б.м.в. в окрестности точки а .
(х) есть б.м.в. в окрестности точки а .
Теоремы о пределах.
Вычисление пределов функций основывается на следующих теоремах:
