Формула полной вероятности. Формула Байеса. Три задачи.
Определение. Говорят, что события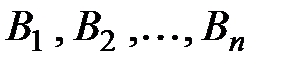 
образуют полную группу событий, если выполнены два условия:
1) 
;
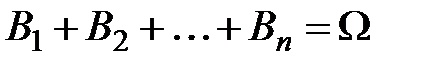2) 
, 
.
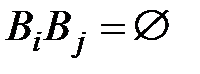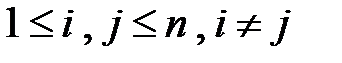Теорема 8.1. Пусть события 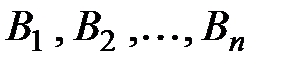образуют полную группу событий. Тогда верны равенства:
1) 
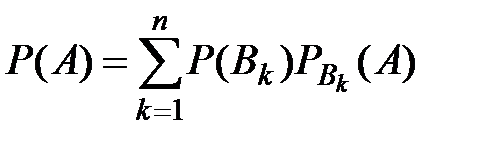(формула полной вероятности);
2) 
, 
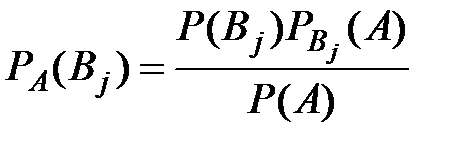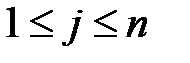(формулы Байеса ).
Пример 8.1. Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения нестандартной детали на первом автомате равна 0,07, а на втором −0,08. Производительность второго автомата втрое больше, чем первого. Найти вероятность того, что наудачу взятая с конвейера деталь нестандартная.
Решение.
Рассмотрим события: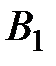 
– деталь изготовлена на 1−ом автомате; 
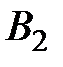– деталь изготовлена на 2−ом автомате. События 
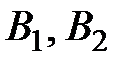образуют полную группу событий. Пусть событие 
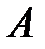− деталь, взятая с конвейера деталь нестандартная. Пусть 
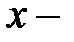число деталей, изготовленных на 1−ом автомате. Тогда 
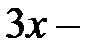число деталей, изготовленных на 2−ом автомате и 
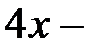число деталей, которые поступают на общий конвейер. Найдем вероятности событий 
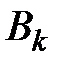, используя формулы классической схемы:
, 
.
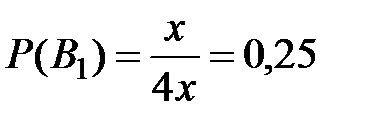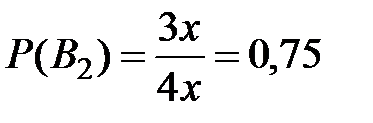Контроль: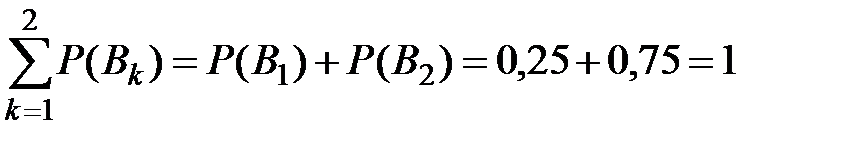 
(верно).
Из условия находим остальные вероятности:
, 
.
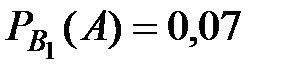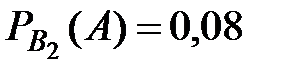По формуле полной вероятности вероятность события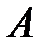 
равна
.
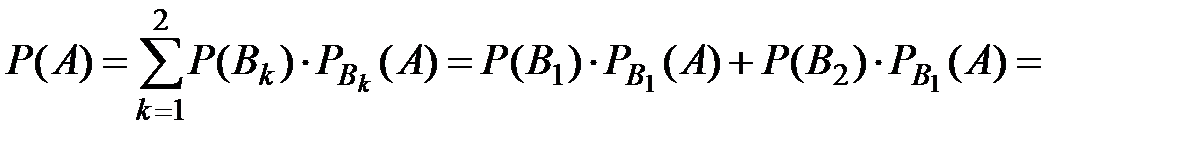
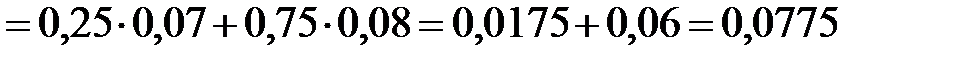Пример 8.2. Имеются две урны. В первой урне 8 белых и 2 черных шара, во второй – 4 белых и 6 черных. Из первой урны, не глядя, берут один шар и кладут его во вторую урну. Из второй урны берут наугад один шар. Найти вероятность того, что этот шар белый.
Решение.
Рассмотрим события: 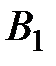– из первой урны взят белый шар; 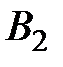– из первой урны взят черный шар. События 
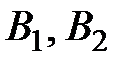образуют полную группу событий. Пусть событие 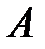−из второй урны взят белый шар. Найдем вероятности событий, используя формулы классической схемы:
; 
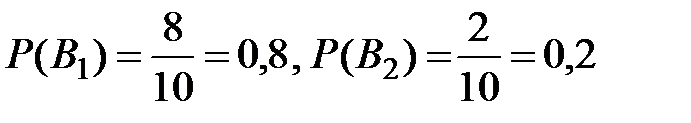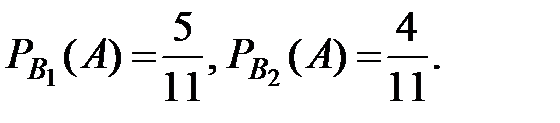
Контроль: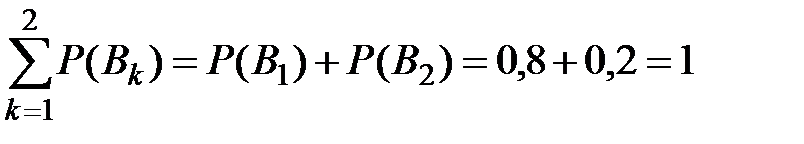 
(верно).
По формуле полной вероятности вероятность события 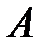равна
.
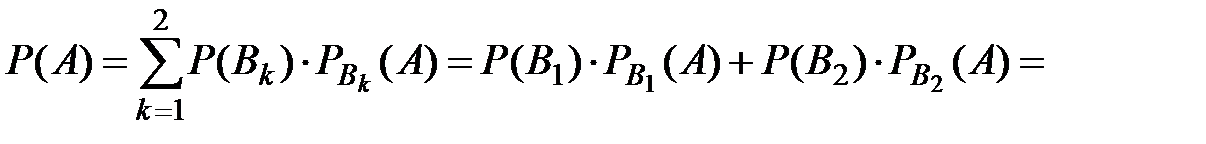
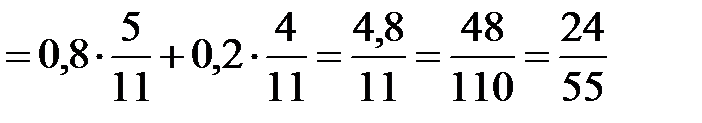Пример 8.3. В трех однотипных ящиках находятся стандартные и нестандартные детали. В первом ящике лежат 3 стандартные детали и 2 нестандартные детали, во втором – 4 стандартные и 1 нестандартная деталь, в третьем – 5 стандартных деталей и 2 нестандартные детали. Из наудачу взятого ящика наудачу извлечена стандартная деталь. Найти вероятность того, что эта деталь лежала в первом ящике.
Решение.
Пусть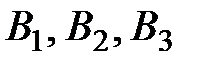 
– события, состоящие в том, что выбран первый, второй, третий ящик соответственно. Пусть событие 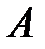− деталь стандартная. События 
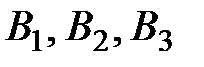образуют полную группу событий. Найдем вероятности событий, используя формулы классической схемы:
;
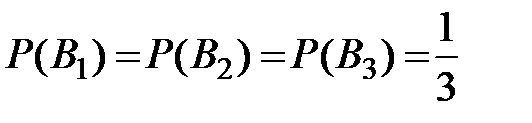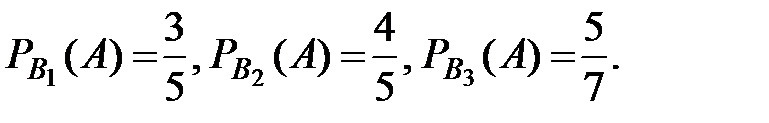
Контроль: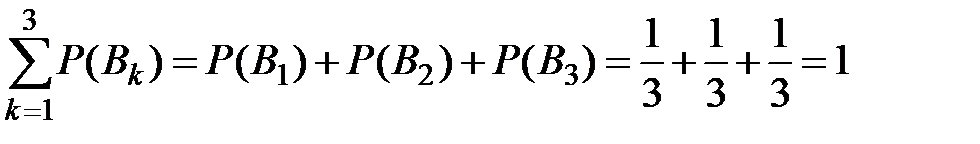 
(верно).
По формуле полной вероятности вероятность события 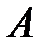равна
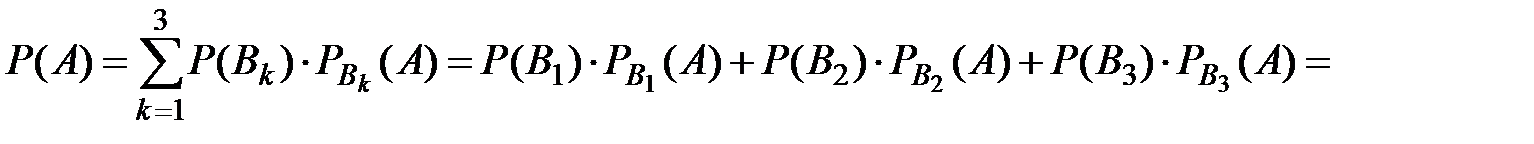
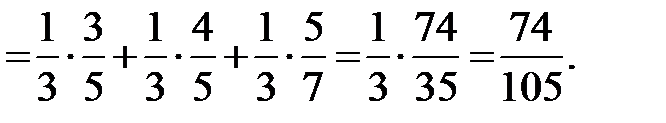
По формуле Байеса
.
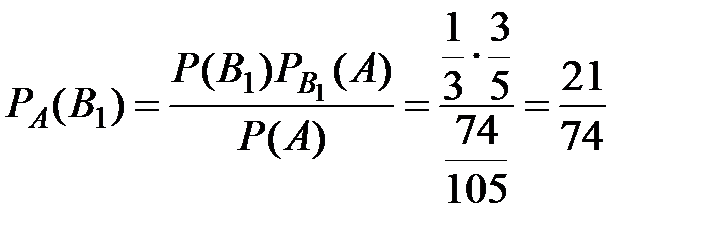Схема Бернулли.
9.1. Основные определения.
Из урны, в которой лежат две буквы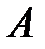 
и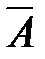 
, последовательно с возвращением вытаскивают 
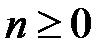одну букву и раскладывают вытащенные буквы по порядку в ряд. Получается слово из букв 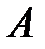и 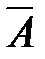, которое является размещением с повторениями из двух элементов по 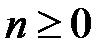элементов. Это слово объявляется элементарным событием. Из комбинаторики следует, что число всех элементарных событий равно 
.
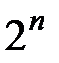Будем вводить вероятность события, пользуясь классической вероятностной схемой с неравновозможными исходами. Для этого достаточно ввести вероятности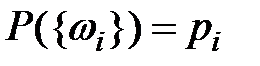 
элементарных событий 
, 
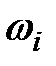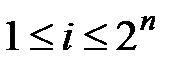. Подробно опишем этот процесс, предполагая для простоты, что 
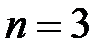. Предположим, что задано число 
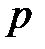, такое, что 
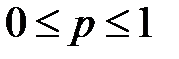и пусть 
.
, 
,
, 
,
, 
,
, 
,
, 
,
, 
,
, 
,
, 
.
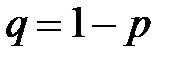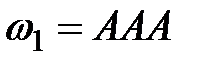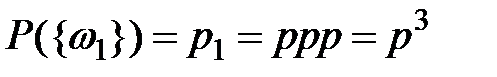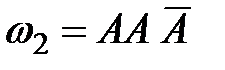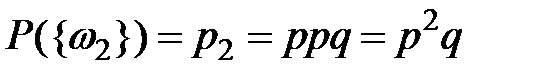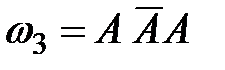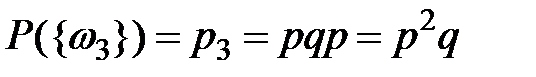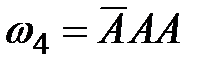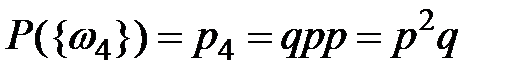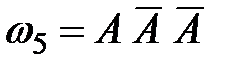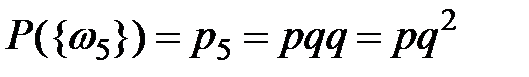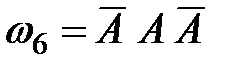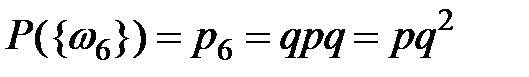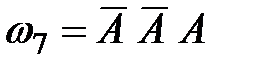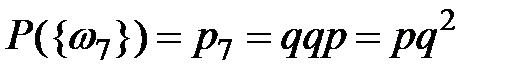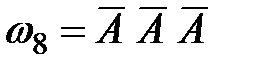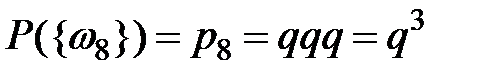Так как
,
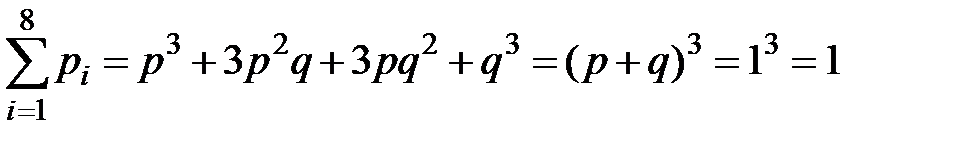то новая вероятностная схема с неравновозможными исходами имеет право на существование. Она называется схемой Бернулли или биномиальной схемой. Совершенно аналогично эта схема определяется при любом .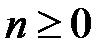
Пример.9.1. Найти вероятность того, что буква 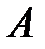будет вытащена последней, если .
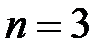Решение.
Введем событие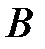 
, которое наступает тогда и только тогда, когда последней будет вытащена буква 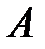. Ясно, что 
.
.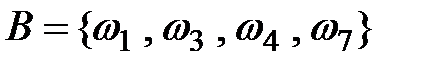
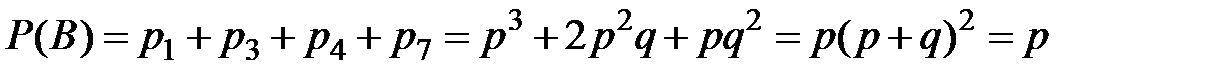