Векторное произведение в координатах.

Найдем формулы вычисления векторного произведения векторов, если векторы заданы координатами:

;

.

По свойствам векторного произведения

=

. (2)

По свойству 1 векторного произведения

, , .

Векторы 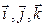образуют правую тройку, круговая перестановка векторов (рис. 3) ориентации не меняет, поэтому

, , .

Перестановка соседних векторов меняет ориентацию (рис. 10), поэтому

, , .

Подставим векторные произведения базисных векторов в равенство (2), получим

.

Последнее равенство есть не что иное, как разложение определителя по первой строке

.

Поэтому

(3)

– формула вычисления векторного произведения в координатах.

Найдем формулу вычисления в координатах площади параллелограмма, построенного на векторах 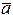и (рис. 5). По формуле (1)

,

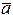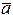т. е. площадь параллелограмма, построенного на векторах и , равна модулю определителя, первая строка которого – базисные вектора, а вторая и третья – координаты векторов и .

Если векторы лежат на плоскости , т.е. , ,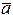

; ,

то площадь параллелограмма, построенного на векторах 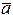и равна

.

Геометрический смысл определителя второго порядка: его модуль равен площади параллелограмма, построенного на векторах, координаты которых расположены в строках определителя.

Пример 1. Даны точки , , . Найти площадь треугольника АВС.

Рис. 11.

Решение. Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах и (рис. 11). Найдем векторы

, .

Тогда из геометрического смысла определителя второго порядка площадь параллелограмма

.

Ответ:

3. Смешанное произведение векторов, его свойства. Признак компланарности векторов. Смешанное произведение в координатах.

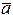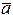Определение2. Смешанным произведением трех векторов , и называется число , равное скалярному произведению вектора на векторное произведение векторов и , то есть

.

Найдем геометрический смысл модуля смешанного произведения. Объем параллелепипеда, построенный на векторах (из рис. 12)

, ,

, .

При этом знак « » необходим, чтобы длина высоты была положительной. Тогда

.

Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах, как на сторонах.

Найдем формулы для вычисления смешанного произведения векторов, если векторы заданы координатами:

, , .

Тогда

.

Скалярное произведение вектора 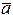на векторное произведение

.

– формула вычисления смешанного произведения в координатах.

Учитывая формулу для вычисления смешанного произведения в координатах, получаем геометрический смысл определителя третьего порядка:

, (4)

модуль определителя равен объему параллелепипеда, построенного на векторах, координаты которых расположены в строках определителя.