Системы линейных уравнений. Формулы Крамера

Для системы трех линейных алгебраических уравнений с тремя неизвестными

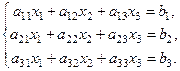(1)

формулы Крамера имеют вид

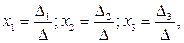
где

, = , = .

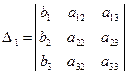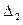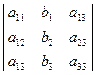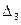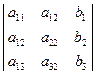Пример 3. Решить по формулам Крамера систему уравнений

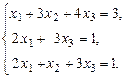
Решение. Главный определитель системы равен

.

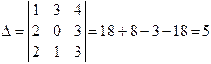Вспомогательные определители:

, ,

.

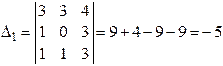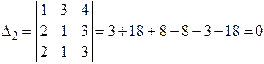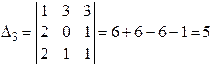Тогда решение системы равно , , .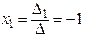

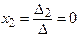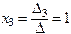Ответ: , ; .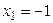

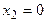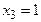Метод Гаусса.

Метод Гаусса заключается в том, что исходную систему путем исключения неизвестный преобразуют к ступенчатому виду. При этом преобразования выполняются над строками в расширенной матрице, так как преобразования, исключающие неизвестные эквивалентны элементарным преобразованиям строк матрицы.

Метод Гаусса состоит из прямого хода и обратного хода. Прямым ходом метода Гаусса является приведение расширенной матрицы системы (1) к ступенчатому виду путем элементарных преобразований над строками. После чего происходит исследование системы на совместность и определенность. Затем по ступенчатой матрице восстанавливается система уравнений. Решение этой ступенчатой системы уравнений является обратным ходом метода Гаусса, в котором, начиная с последнего уравнения, последовательно вычисляются неизвестные с большим порядковым номером, и их значения подставляются в предыдущее уравнение системы.

Исследование системы в конце прямого хода происходим по теореме Кронекера-Капелли сравнением рангов матрицы системы А и расширенной матрицы А´. При этом возможны следующие случаи.

1) Если 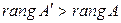, то система несовместна (по теореме Кронекера-Капелли).

2) Если 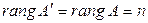, то система (1) является определенной, и наоборот (без доказательства).

3) Если 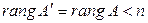, то система (1) является неопределенной, и наоборот (без доказательства).

Неравенство 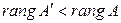не имеет места, так как матрица А является частью матрицы А´, неравенство 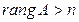не имеет места, так как число столбцов матрицы А равно п. Кроме того, для системы с квадратной матрицей, то есть если п = т, равенства 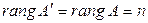равносильны тому, что .

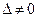Если система является неопределенной, то есть выполняется 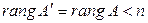, то некоторые ее неизвестные объявляются свободными, а остальные через них выражаются. Количество свободных неизвестных равно . При выполнении обратного хода метода Гаусса, если в очередном уравнении после подстановки найденных ранее переменных, неизвестных осталось более одного, то свободными неизвестными объявляются любые неизвестные, кроме одного.

Рассмотрим реализацию метода Гаусса на примерах.

Пример 4. Решить систему уравнений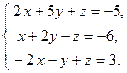

Решение. Решим систему методом Гаусса. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду элементарными преобразованиями строк (прямой ход).

~ ~ ~

~ ~ .

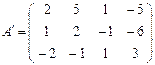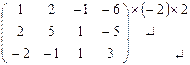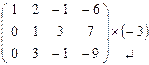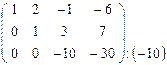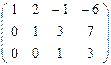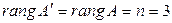, поэтому система совместна и имеет единственное решение, т.е. является определенной.

Составим систему ступенчатого вида и решим ее (обратный ход).

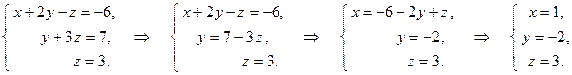
Проверку легко сделать подстановкой.

Ответ: .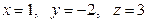

Тема 2. Векторная алгебра.