Топологический язык на прямой.

Окрестность точки.

Определение.

Пусть 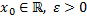. 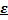- окрестностью точки 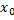называют множество

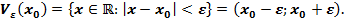
Проколотой 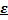- окрестностью точки 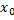называют множество

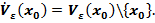
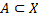Если в течении достаточно большого промежутка времени фиксировано множество , в котором рассматриваются точки , дополнением множества (до пространства ) называют множество

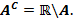
Внутренние, внешние и граничные точки

Определение.

Пусть .

Точка 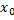– внутренняя точка множества , если у неё существует окрестность, которая целиком содержится в множестве , т.е.

Замечание.

Если 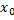– внутренняя точка множества , то .

Определение.

Пусть .

Точка 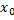– внешняя точка множества , если у неё существует окрестность, которая целиком содержится в дополнении множества , т.е.

Замечание.

Если 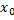– внешняя точка множества , то .

Определение.

Пусть .

Точка 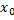– граничная точка множества , если она не является не внутренней, не внешней точкой, т.е. у любой окрестности 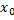существуют как точки множества, так и точки его дополнения:

Определение.

Внутренность множества – множество всех его внутренних точек,

Определение.

Внешность множества – множество всех его внешних точек,

Определение.

Граница множества – множество всех его граничных точек,

Изолированные точки и точки сгущения

Определение.

Пусть .

Точка 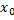– изолированная точка множества ,

если существует окрестность, содержащая лишь одну эту точку множества

Определение.

Пусть .

Точка 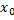– точка сгущения множества ,

n если любая её окрестность содержит бесконечно много точек множества , т.е.

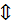
n если в любой её проколотой окрестности существует хотя бы 1 точка множества , т.е.

Доказательство равносильности.

Часть.

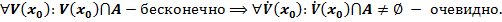
Часть.

.

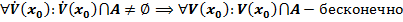Предположим от противного:

Пусть для 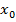выполнено условие: 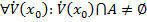, и при этом существует окрестность точки 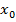, пересекающаяся с множеством 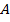по конечному множеству точек, т.е.

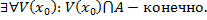
Занумеруем точки пересечения:

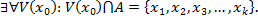
Выберем минимальное из расстояний между точкой 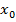и точками 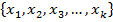, т.е.

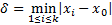
Тогда

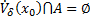
Получаем противоречие.

Замечания.

I. Изолированная точка множества не просто принадлежит множеству , но и является его граничной точкой.

II. Точки сгущения – предельные точки множества.

III. Точка сгущения может как принадлежать множеству , так и не принадлежать ему.

IV. Внешняя точка множества не может быть точкой сгущения.

V. Изолированная точка множества не может быть точкой сгущения.

Привести примеры к замечаниям.

Обозначение.

Множество всех предельных точек множества (всех его точек сгущения) называют производным множеством множества и обозначают

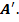
Задача.

Заполнить таблицу.

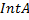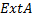				Изолированные точки

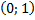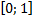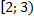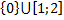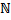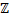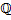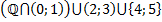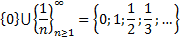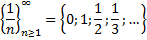Открытые множества

Определение.

Множество 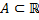называется открытым, если каждая его точка – внутренняя точка множества .

Замечание.

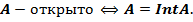
Теорема.

Открытое множество на прямой – объединение некоторого семейства лучей и интервалов.

Свойства открытых множеств.

Теорема 1.

Объединение любого семейства открытых множеств открыто.

Доказательство.

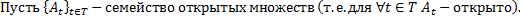
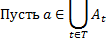
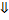
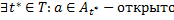
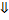
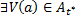
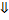
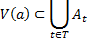
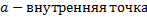
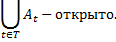
Замечание.

Пересечение любого семейства открытых множеств не обязано быть открытым.

Приведите пример.

Теорема 2.

Пересечение конечного числа открытых множеств открыто.

Доказательство.

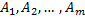– открытые множества.

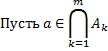
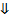
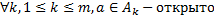
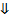
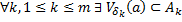
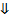
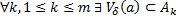
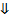
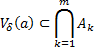
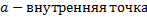
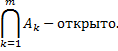
Замкнутые множества

Определение.

Множество 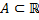называется замкнутым,

n если оно содержит все свои конечные точки сгущения, т.е. .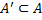

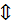
n если его дополнение открыто.

Доказательство равносильности.

1 часть. .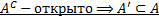

Предположим от противного:

Пусть 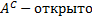, при этом существует хотя бы ода предельная точка, не содержащаяся в :

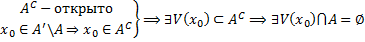
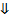
То есть, в окрестности 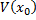нет ни одной точки множества .

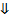
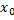не является точкой сгущения

(любая точка дополнения входит в некоторую окрестность)

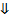
Противоречие с условием .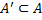

2 часть. .

Пусть