С помощью указанных примеров мы можем получить разнообразные результаты в тех конструктивных построениях прямых линий, кото рые мы компануем

 |
В. Конструктивное разрешение в композициях кривых представляет собою особый интерес, вследствие обилия компози ционных возможностей: всякой кривой линии мы можем придать тот изгиб, который нам желателен для данной композиции. Кроме того, в композициях кривых следует обратить внимание на присущую им плавность упругого изгиба, обладающего динамическими свойствами. Эти динамические свойства особенно усиливают степень конструк тивности наших построений и, тем самым, вызывают в нас желание
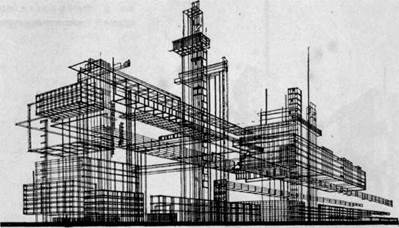 |

Завод тяжелой кн дустрии. Простран ственно-г рафиче

ская задача»-—
широко использовать динамику изгиба. По внешним признакам кон структивные композиции кривых можно подразделить на следующие виды сочетания:
I. Узловое.
II. Спиральное.
