Интегрирование по частям
Лекция 36. Основные методы интегрирования. Замена переменного (способ подстановки). Интегрирование по частям. Интегралы от некоторых функций, содержащих квадратный трехчлен.
Основные методы интегрирования
Основных методов интегрирования, то есть основных методов вычисления неопределенных интегралов, четыре:
1) Непосредственное интегрирование.
2) Интегрирование с помощью подстановки (с помощью замены переменной интегрирования).
3) Интегрирование по частям.
4) Приближенное интегрирование.
1.Непосредственное интегрирование.
Этот метод основан на тождественных преобразованиях подынтегральной функции с последующим применением свойств неопределенных интегралов и таблицы основных неопределенных интегралов.
Пример 1. Вычислить 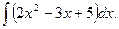
Решение. Оно очевидно:
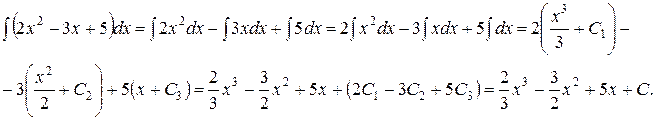
Итак, 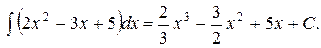
Здесь С - неопределенная константа, представляющая собой комбинацию 2С1-3С2+5С3 неопределенных констант (С1; С2; С3).
Проверка:
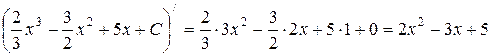 - верно.
- верно.
Этот пример показывает, что при разбиении неопределенного интеграла на сумму или разность нескольких неопределенных интегралов, появляется и несколько неопределенных констант. Но они затем объединяются в одну неопределенную константу. Поэтому при записи суммы или разности нескольких интегралов их неопределенные константы можно не писать, а записать лишь одну общую неопределенную константу С в самом конце.
Пример 2. Вычислить 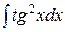 .
.
Решение:
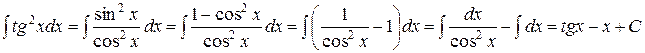 .
.
Проверка:
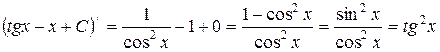 - верно.
- верно.
2. Интегрирование с помощью подстановки (с помощью замены переменной интегрирования).
Суть этого метода в следующем. Пусть требуется вычислить некоторый неопределенный интеграл 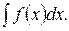 Нередко его можно упростить, сведя к табличному, путем замены переменной интегрирования х на какую-то новую переменную (на переменную t), используя подходящую подстановку x =
Нередко его можно упростить, сведя к табличному, путем замены переменной интегрирования х на какую-то новую переменную (на переменную t), используя подходящую подстановку x = 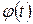 , где
, где 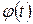 - некоторая дифференцируемая функция. Тогда получим следующую схему вычисления неопределенного интеграла с помощью подстановки:
- некоторая дифференцируемая функция. Тогда получим следующую схему вычисления неопределенного интеграла с помощью подстановки:
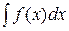 =
= 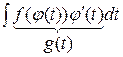 =
= 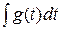 =
= 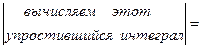
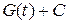 = =
= = 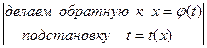 =
= 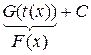 =
= 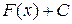
Естественно, что применяемая подстановка будет оправданной лишь в том случае, если полученный в результате ее применения интеграл 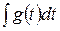 будет проще, чем исходный интеграл
будет проще, чем исходный интеграл 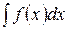 .
.
Примечание. В практических случаях чаще удобнее делать не подстановку вида 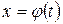 , а подстановку вида
, а подстановку вида 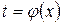 .
.
Пример 3. Вычислить 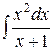 .
.
Решение:
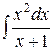 =
= 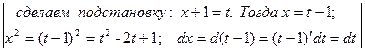 =
= 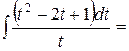
= 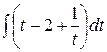 =
= 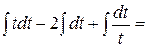
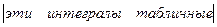 =
=
= 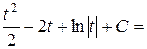
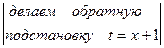
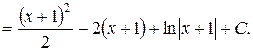
Пример 4. Вычислить 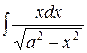 .
.
Решение:
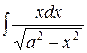 =
= 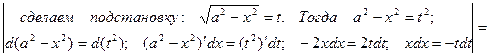
= 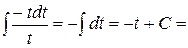
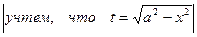
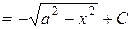 .
.
Пример 5. Вычислить 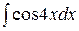 .
.
Решение:
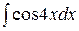 =
= 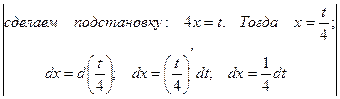 = =
= = 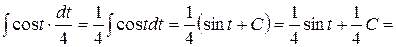 =
= 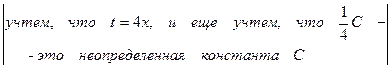
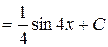 .
.
Пример 6. Вычислить 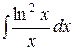 .
.
Решение:
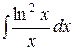 =
= 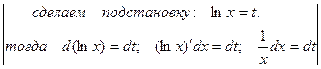 =
= 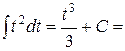 =
= 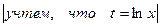
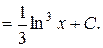
Пример 7. Вычислить 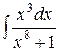 .
.
Решение:
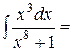
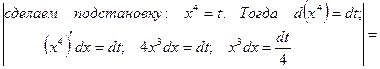
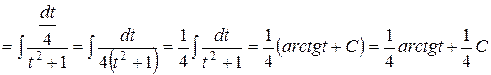 =
= 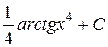
Интегрирование по частям
Этот метод основан на использовании формулы
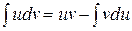 , (1)
, (1)
которая называется формулой интегрирования по частям. В этой формуле 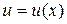 и
и 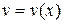 - любые две дифференцируемые функции, для которых существуют и
- любые две дифференцируемые функции, для которых существуют и 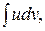 и
и 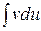 .
.
Докажем эту формулу. Опираясь на формулу для дифференциала произведения двух функций
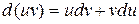
и интегрируя обе части этого равенства, получим:
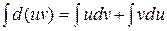
Применяя теперь свойство 3 неопределенных интегралов к интегралу слева, получим:
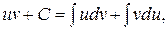 откуда
откуда 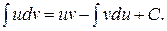
В правой части 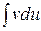 даст, после своего вычисления, некоторую функцию плюс неопределенную константу. Вместе с уже имеющейся там неопределенной константой С этих констант в правой части окажется две. Поэтому одну из них (а именно, константу С) можно отбросить, так как эти две константы все равно объединятся в одну. В итоге как раз и получим формулу (1)
даст, после своего вычисления, некоторую функцию плюс неопределенную константу. Вместе с уже имеющейся там неопределенной константой С этих констант в правой части окажется две. Поэтому одну из них (а именно, константу С) можно отбросить, так как эти две константы все равно объединятся в одну. В итоге как раз и получим формулу (1)
Примечание . При вычислении 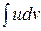 по формуле интегрирования по частям (1) нам придется вычислить два неопределенных интеграла (выполнить работу, состоящую из двух частей). Сначала по имеющемуся дифференциалу
по формуле интегрирования по частям (1) нам придется вычислить два неопределенных интеграла (выполнить работу, состоящую из двух частей). Сначала по имеющемуся дифференциалу 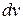 функции
функции 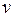 нужно будет найти саму функцию
нужно будет найти саму функцию 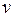 . Для этого используем формулу (8):
. Для этого используем формулу (8):
если 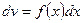 , то
, то 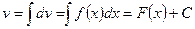 (2)
(2)
Таким образом, получаем: 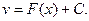 То есть, получаем не одну, а множество функций
То есть, получаем не одну, а множество функций 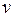 . Но нам нужна лишь одна из них (любая). Проще всего получить ее, отбросив в (2) константу С:
. Но нам нужна лишь одна из них (любая). Проще всего получить ее, отбросив в (2) константу С:
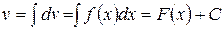 =
= 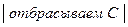 = F(x) (3)
= F(x) (3)
По этой схеме находится функция 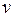 . Затем, в соответствии с формулой (1), нужно выполнить вторую часть работы - вычислить интеграл
. Затем, в соответствии с формулой (1), нужно выполнить вторую часть работы - вычислить интеграл 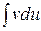 .
.
Формулу (1) для вычисления 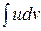 по частям есть смысл применять, если можно вычислить оба интеграла: и
по частям есть смысл применять, если можно вычислить оба интеграла: и 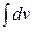 , и
, и 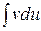 .
.
Пример 8. Вычислить 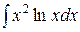 .
.
Решение.
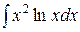
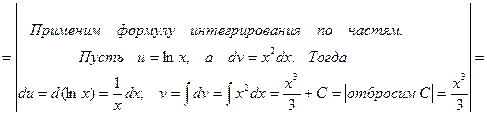 =
= 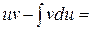
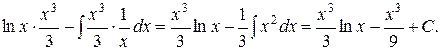
Пример 9. Вычислить 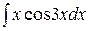 .
.
Решение.
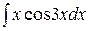 =
= 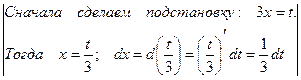 =
=
= 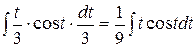 =
= 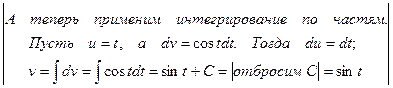 =
= 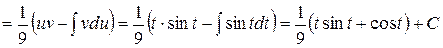 =
=
= 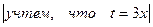 =
= 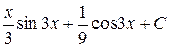 .
.
В примере 9 применены и подстановка, и интегрирование по частям.
В заключение укажем следующее. Проблема вычисления неопределенных интегралов – гораздо более сложная, чем проблема вычисления производных. Среди неопределенных интегралов и много неберущихся. Однако доказана теорема: если функция 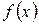 непрерывна на некотором промежутке оси ох (например, на отрезке
непрерывна на некотором промежутке оси ох (например, на отрезке 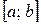 оси ох), то на этом промежутке существует и
оси ох), то на этом промежутке существует и 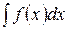 , то есть существует множество первообразных F(x)+C для подынтегральной функции f(x). Но только не всегда эти первообразные можно выразить через элементарные функции. В этих случаях (случаях неберущихся интегралов) применяют приближенное интегрирование. О приближенном интегрировании мы поговорим позже.
, то есть существует множество первообразных F(x)+C для подынтегральной функции f(x). Но только не всегда эти первообразные можно выразить через элементарные функции. В этих случаях (случаях неберущихся интегралов) применяют приближенное интегрирование. О приближенном интегрировании мы поговорим позже.
