Системы линейных однородных уравнений

Метод Гаусса.

Одним из наиболее универсальных и эффективных методов решения систем линейных уравнений является метод Гаусса, состоящий в последовательном исключении неизвестных.

Пусть дана система линейных уравнений, содержащая 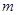уравнений и 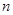неизвестных:

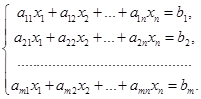
Метод Гаусса состоит из двух этапов: прямой ход и обратный ход.

Прямой ход. Приводим систему линейных уравнений к ступенчатому виду.

При этом удобно работать с соответствующей расширенной матрицей 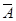. Приводим ее к ступенчатому виду при помощи элементарных преобразований над строками матрицы и по нему записываем уже ступенчатую систему линейных уравнений, которая будет эквивалентна исходной системе.

Обратный ход. Решаем ступенчатую систему.

Если в ступенчатой системе имеются уравнения 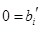, где 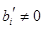, то система несовместна, а если таких уравнений нет, то система совместна и подлежит дальнейшему решению. Все уравнения вида 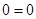можно отбросить.

В последнем уравнении системы выражаем первое присутствующее слева неизвестное через последующие присутствующие неизвестные этого уравнения. Затем, повторяем те же действия с предпоследним уравнением, предварительно подставив в него выраженное неизвестное из последнего уравнения. Далее, аналогичным образом, поднимаемся вверх по всем уравнениям системы, предварительно подставив в них полученные выражения из всех уравнений ниже.

Таким образом, получаем общее решение исходной системы линейных уравнений. Предавая переменным, стоящим в правых частях равенств общего решения системы произвольные значения, получим частные решения исходной системы.

Например, решить систему 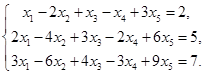методом Гаусса.

Решение: приведем расширенную матрицу 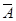к ступенчатому виду при помощи элементарных преобразований над строками матрицы:

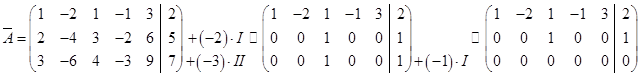
Запишем ступенчатую систему:

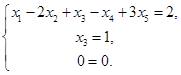
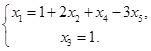
Ответ: общее решение системы: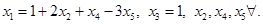

Системы линейных однородных уравнений.

Пусть дана однородная система линейных уравнений, содержащая 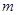уравнений и 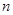неизвестных:

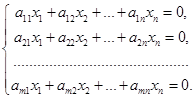
Однородная система всегда совместна, так как 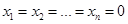всегда является ее решением. Это решение называется нулевым или тривиальным.

При каких условиях однородная система имеет и ненулевые решения?

Теорема. Однородная система линейных уравнений имеет ненулевые решения тогда и только тогда, когда ранг основной матрицы системы меньше числа неизвестных, т.е. .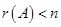

Теорема. Однородная квадратная система линейных уравнений имеет ненулевые решения тогда и только тогда, когда определитель основной матрицы системы равен нулю, т.е. .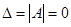

Универсальным методом решения однородных систем линейных уравнений является метод Гаусса.

Например, решить однородную систему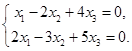

Решение: решим данную систему методом Гаусса.

Приведем расширенную матрицу 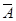к ступенчатому виду при помощи элементарных преобразований над строками матрицы:

.

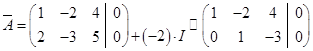Запишем ступенчатую систему:

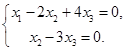
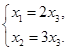
Ответ: общее решение системы: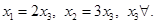

Контрольные вопросы:

1. Что называется элементарными преобразованиями системы линейных уравнений?

2. Какая система линейных уравнений называется ступенчатой?

3. В чем заключается метод Гаусса?

4. Сформулируйте определение однородной системы линейных уравнений.

5. Какое решение однородной системы линейных уравнений называется тривиальным?

6. Каждая ли однородная система линейных уравнений имеет тривиальное решение?

7. В каком случае однородная система линейных уравнений имеет нетривиальные решения?

8. В каком случае однородная квадратная система линейных уравнений имеет нетривиальные решения?

9. Как решать однородные системы линейных уравнений?