Симплекс – алгоритм (2-й этап симплекс – метода)

Основная теорема симплекс-метода.

Симплекс – метод состоит из двух этапов:

1)нахождение исходного опорного решения ЗЛП;

Нахождение оптимального решения. Этот этап носит название симплекс - алгоритм.

Нахождение исходного опорного решения (1-й этап симплекс-метода).

Рассмотрим ЗЛП в стандартной форме, при этом неизвестные в целевой функции перенесем влево и рассмотрим следующую задачу.

Найти значения

x_j ≥ 0, j = 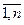и max Z, (1.1)

удовлетворяющие условиям:

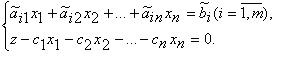(1.2)

(1.3)

Замечание.Свободный член в уравнении целевой функции равен нулю, но он может быть, и отличен от нуля.

Будем считать, что система (1.1) ,(1.2) совместна, система уравнений (1.2) – линейно независима и все .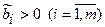

Найдем опорное решение системы (1.2), совершив последовательность симплексных преобразований, и пусть при этом i-е уравнение системы (1.2) оказалось разрешенным относительно переменнойx_i (i = ):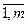

x_i + a_im+1x_m+1 + a_im+2x_m+2 + ... + a_isx_s + ... + a_inx_n = b_i (i = 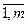), (1.4)

где все b_i >0(i = ).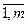

Базисными переменными являются переменные x₁, x₂, ... , x_m, а свободными: x_m+1, x_m+2, ... , x_s , ... , x_n(базисными могут быть и не обязательно первые m переменных). Исходное невырожденное опорное решение системы (4.4) имеет вид:

X₀ =(b₁, b₂, ... , b_m, 0, 0, ... , 0).

Будем говорить, что система уравнений (4.4) приведена к опорному решению. Исключим из уравнения (4.3) базисные переменные. Для этого каждое i-е уравнение системы (1.4) умножим на с_i и затем все полученные уравнения сложим, получим:

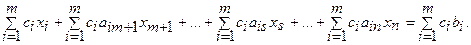(1.5)

Уравнение (4.3) запишем следующим образом:

Z– 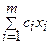– c_m+1x_m+1 – ... – c_sx_s – ... – c_nx_n = 0.

Складывая это уравнение с (4.5), получим:

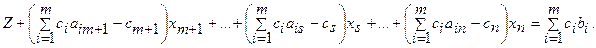
Обозначим: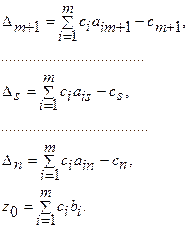

Тогда уравнение целевой функции будет иметь вид

Z+ Δ_m+1x_m+1 + ... + Δ_sx_s + ...+ Δ_nx_n = Z_o.(1.6)

Уравнение (4.6) будем называть уравнением целевой функции, приведенным к свободным переменным, а коэффициенты Δ_j (j = 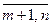) – оценками свободных переменных, где

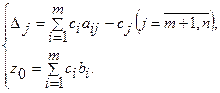(1.7)

В результате этих преобразований ЗЛП (1.1) - (1.3) приведена к следующей эквивалентной задаче: найти значения

x_j ≥ 0, j = 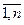и max Z,(1.1)

удовлетворяющие условиям.

(1.4)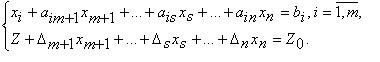

(1.6)

Задачу (1.1), (1.4), (1.6) будем называть ЗЛП в канонической форме или в каноническом виде.

Система ограничений этой задачи приведена к опорному решению:

X₀ =(b₁, b₂, ... , b_m, 0, 0, ... , 0) и Z(X₀) = Z₀.

Уравнение целевой функции приведено к свободным переменным.

Замечание.Уравнение (1.6) добавим к системе уравнений (1.4) и рассмотрим систему из (m + 1) уравнений, при этом в уравнении (1.6) базисной является свободная

переменная Z.

Симплекс – алгоритм (2-й этап симплекс – метода).

В задаче (1.1), (1.4), (1.6) полагаем равными нулю свободные переменные и получаем исходное опорное невырожденное решение (невырожденный план):

X₀= (b₁, b₂, ... , b_m,0, 0, ... , 0) и Z(X₀)= Z₀.

Теперь от этого решения (плана) надо перейти к другому опорному решению (плану) X₁с бóльшим значением целевой функции, чем z₀, т.е. Z(Х₁) > Z(Х₀) = Z₀.

Допустим, что для этого мы хотим ввести в базис свободную переменную x_s = 0, т.е. хотим увеличить значение x_s. При этом в s-м столбце обязательно должен быть хотя бы один коэффициент a_is > 0. Выбираем s-й столбец разрешающим.

Переходим от одного опорного решения к другому. Для этого необходимо разрешающую строку выбирать по правилу

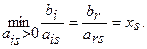
т.е. в качестве разрешающей будет строка r, а в качеству разрешающего элемента: a_rs.

С разрешающим элементом a_rs выполним преобразование системы уравнений (1.4) и (1.6) по формулам полного исключения неизвестных (метода Жордана – Гаусса) и найдем новое опорное невырожденное решение Х₁ со значением целевой функции:

Z(Х₁) = Z₀ – Δ_sx_s.(1.8)

Если Δ_s < 0, то « – Δ_sx_s» > 0и новое значениеZ(X₁), будет больше, чем z₀ на величину « – Δ_sx_s» > 0.

Теперь сформулируем правила выбора разрешающего элемента в симплекс – алгоритме:

1. В базис вводим свободную переменную x_sс отрицательной оценкой Δ_s < 0, если среди коэффициентов a_is есть хотя бы один положительный, т.е.a_is > 0. Это правило выбора разрешающего столбца s.

2. Из базиса выводим переменную x_r по правилу

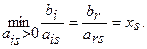
Это правило выбора разрешающей строки r.

3. С разрешающим элементом a_rs выполним преобразование системы (1.4), (1.6).

Коэффициенты при неизвестных a΄_ij, Δ΄_j и значения b΄_j, z΄₀ в новой системе уравнений вычисляются по формулам:

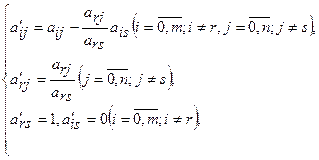(1.9)

где введены обозначения:

b΄_i = a΄_i0,Δ΄_j = a΄_0j, Z΄₀ = a΄_00.

Действия, выполненные в пп. 1-3 составляют одну операцию симплекс – алгоритма, выполнив которую, мы перейдем от опорного решения Х₀к Х₁, при этом Z(Х₁)>Z(Х₀) = Z₀.

Вычислим ΔZ= Z(Х₁)– Z(Х₀) = – Δ_sx_s > 0,откуда Δ_s = – Δ_z/x_s.

Таким образом, коэффициент Δ_s характеризует изменение целевой функции Z, приходящееся на каждую единицу изменения переменной x_s, т.е. он оценивает изменение целевой функции Z. Поэтому коэффициенты Δ_j и называются оценками свободных переменных.

Выполнив одну операцию, можем переходить к следующей, и после ряда итераций мы получим оптимальное решение или убедимся в неограниченности целевой функции. Эти признаки устанавливает основная теорема симплексного метода.

Формулировка: Если после выполнения очередной итерации:

1) найдется хотя бы одна отрицательная оценка Δ_s < 0 и в каждом столбце с такой оценкой будет хотя бы один положительный элемент a_is > 0, то можно улучшить решение, выполнив следующую итерацию;

2) найдется хотя бы одна отрицательная оценка Δ_s < 0, столбец которой не содержит положительных элементов, т.е. все a_is ≤ 0 (i = 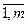), то целевая функция z неограниченна в области допустимых решений, т.е. Z_max → ∞;

3) все оценки Δ_j ≥ 0 (j = 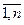), то получено оптимальное решение.

Решение конкретных ЗЛП будем проводить в таблицах, аналогичных таблицам Гаусса, которые называются симплексными (сокращенно симплекс – таблицами).

Доказательство:

1) Выберем разрешающий элемент согласно пунктам 1 – 3 и перейдем к новому опорному решению Х₁, для которого значение Z(Х₁) больше, чем z₀ на величину «– Δ_sx_s»>0. Следовательно, новое опорное решение будет лучше предыдущего.

2) Пусть Δ_s<0 и все a_is ≤ 0, i = 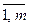, тогда если переменную X_s ввести в базис, то функция Z увеличится на величину ΔZ = – Δ_sx_s >0.

При наличии a_is>0 величина X_s ограничивается минимумом отношений 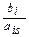для a_is>0. Если же все a_is≤0 , то значение X_s можно не ограничивать, т.к. при любом сколь угодно большом значении X_s, значения всех остальных базисных переменных X_i всегда будут неотрицательными, т.к X_i = b_i – a_isX_s и при a_is ≤ 0, X_i всегда положительны.

Таким образом, переменной X_s можно придавать сколь угодно большое значение и при этом целевая функция z будет достигать тоже сколь угодно большого значения, т.е. Z_max → ∞.

3) Если все оценки Δ_j ≥ 0, то т. к. Z(Х₁) = Z₀ – Δ_sx_s, следует, что увеличивая любую свободную переменную мы будем уменьшать значение целевой функции Z. Отсюда следует, что ни при каком другом допустимом решении функция Z не может быть увеличена, т.е. найденное решение является оптимальным. Теорема доказана.