Внутренние силы. Механическое напряжение

Внутренние силы являются приращением сил взаимодействия между частями одного и того же тела, возникающим при его нагружении.

Пусть произвольное тело рассечено плоскостью на две части и в этом сечении для одной из частей в произвольной точке выделена малая площадка , ориентация которой в пространстве определяется нормалью площадки n (рис. 1.4а). Тогда средняя интенсивность на площадке . При стягивании площадки в точку: .

Интенсивность внутренних сил , передающихся в точке через выделенную площадку, называется механическим напряжением на данной площадке. Его размерность: . На основании третьего закона Ньютона на вторую часть рассеченного тела действует точно такое же напряжение.

Разложив вектор полного напряжения на нормаль и касательное направление в площадке , получим - нормальное и - касательное напряжения на площадке с нормалью (рис. 1.4б).

Выделим в окрестности рассматриваемой точки бесконечно-малый элемент в форме параллелепипеда со сторонами . Действующие в каждой из его граней полные напряжения можно представить как геометрическую сумму одного нормального и двух касательных напряжений (рис. 1.4в). Возникающие при этом 9 величин, можно объединить в тензор напряжений: . На главной диагонали тензора напряжений находятся нормальные напряжения, а касательные напряжения расположены слева и справа от нее. Индекс у нормальных и первый индекс у касательных напряжений определяет нормаль к площадке, в которой они действуют, а второй индекс – ось параллельно которой они действуют. Тензор однозначным образом характеризует напряженное состояние тела в данной точке и его 9 координат (напряжения) меняются по определенному закону при смене системы координат.

1.5 Принцип суперпозиции

Линейно-деформируемая система – система, в которой внутренние усилия, напряжения, деформации и перемещения прямо пропорциональны действующей нагрузке. Система, имеющая линейную диаграмму деформирования, называется физически-линейной. Система, в которой изменениями размеров и формы, возникающими вследствие деформации, можно пренебречь является геометрически-линейной.

Определение внутренних сил с учетом влияния перемещений называется расчетом по деформированному состоянию. В дальнейшем все системы будут линейно-деформируемыми.

Принцип суперпозиции (независимости действия сил): результат действия группы сил равен сумме (алгебраической или геометрической) результатов, полученных от действия каждой из сил в отдельности. Принцип суперпозиции справедлив для линейно-деформируемых систем (рис. 1.5): суммарное перемещение под действием системы сил и можно определить как алгебраическую сумму перемещений от действия силы и силы в отдельности.

1.6 Метод сечений

Метод сечений предназначен для определения значений и направления действия внутренних сил.

Внутренние силы, распределенные по сечению, можно привести к главному вектору , приложенному в центре тяжести сечения и главному моменту (рис. 1.6б). Каждый из этих векторов можно разложить на 3 компоненты по осям координат: 3 силы ( ) и 3 момента ( ), которые называются внутренними усилиями или силовыми факторами в поперечном сечении.

Названия внутренних усилий:

– продольная (осевая) сила, вызывающая деформацию растяжения или сжатия по оси стержня;

– поперечные (перерезывающие) силы, вызывающие сдвиг поперечных сечений относительно друг друга;

– изгибающие моменты в сечении относительно осей и , возникающие при изгибе в плоскостях и соответственно;

– крутящий момент, возникающий при взаимном повороте сечений вокруг оси стержня.

Связь внутренних усилий и напряжений:

Предполагая напряжения известными в каждой точке поперечного сечения, умножив их на площадь элементарной площадки , а также на расстояния до осей для моментов и проинтегрировав по всей площади сечения, получим

Последовательность его применения:

1) рассматриваемое тело освобождаем от связей, заменяя их действие, на действие соответствующих реакций (рис. 1.6а).

2) в том месте, где предполагается определять внутренние силовые факторы, тело мысленно рассекается плоскостью, перпендикулярной его оси.

3) любая из двух частей тела, полученная при рассечении, мысленно отбрасывается.

4) систему сил, действующих в рамках отброшенной части тела (внешние силы и реакции связей), заменяем эквивалентной системой сил, приложенной к оставшейся части конструкции, в месте рассечения в точке соответствующей центру тяжести сечения (рис. 1.6б).

5) составляем в общем случае 6 уравнений статического равновесия для оставшейся части с учетом всех сил на нее действующих и системы сил, появившихся в месте рассечения.

6) неизвестные внутренние усилия определятся из полученных уравнений статического равновесия оставшейся части:

Графики изменения внутренних усилий вдоль оси стержня называются эпюрами.

При построении эпюр вначале определяются границы участков, которыми являются: точки, где приложены внешние сосредоточенные усилия (момент, сила) или начинает или заканчивает действовать распределенная нагрузка, а также точки, где изменяется поперечное сечение стержня.

Правила построения эпюр:

1) Применяя метод сечений, с учетом правила знаков, получают аналитические зависимости для всех существующих внутренних усилий для каждого из участков;

2) Ординаты эпюр в определенном масштабе откладывают от базисной линии, проводимой параллельно оси стержня;

3) Полученную эпюру штрихуют линиями, перпендикулярными базисной линии;

4) Для характерных ординат на эпюрах откладываются их значения, а в кружочке – знак усилия.

Поперечные сечения, в которых действуют наибольшие напряжения, определяют опасные сечения (в них наиболее вероятно разрушение).

1.7 Основные типы опор. Реактивные усилия

1) шарнирно-подвижная опора – устройство, позволяющее перемещение опорного сечения параллельно опорной плоскости и поворот его в вертикальной плоскости относительно оси цилиндрического шарнира, но не дающего возможности перемещения в направлении наложенной связи по вертикали. Реакция такой опоры направлена вдоль опорной связи (рис. 1.7а);

2) шарнирно-неподвижная опора не допускает смещений опорного сечения ни в продольном, ни в поперечном направлениях, но допускает поворот этого сечения относительно шарнира. На данной опоре возникают две реакции, направленные по оси балки и перпендикулярно оси балки (рис. 1.7б);

3) жесткое закрепление (заделка) не допускает поворота опорного сечения и перемещения его ни в каком направлении, т.е. на такой опоре возникают три реакции – вертикальная и горизонтальная реакции и изгибающий момент (рис. 1.7в).

Типы балок:

1) консоль – балка с одним жестко защемленным концом и другим свободным концом;

2) простая – однопролетная балка, имеющая по концам шарнирные опоры, расстояние между которыми называется пролетом балки;

3) консольная – простая балка, имеющая одну или две консоли.

Недопустимо соединение балки с основанием при помощи шарнирных опор, направления которых были бы параллельны друг другу или пересекались в одной точке (в противном случае конструкция будет геометрически-изменяемой). Геометрически неизменяемые системы, в которых опорные реакции и внутренние усилия могут быть найдены из одних только уравнений статического равновесия, называются статически определимыми.

В случае если число наложенных на систему связей больше числа уравнений равновесия система является статически-неопределимой.

1.8 Условие прочности и задачи, решаемые с его помощью

Условие прочности - максимальное по абсолютной величине действующее в конструкции напряжение не должно превышать определенного заданного значения: , где

- допускаемое напряжение (задается при расчете конструкции),

-опасные для данного материала напряжения (определяются экспериментально),

- коэффициент запаса прочности;

Выбор коэффициента запаса прочности определяется

- учетом конкретных условий работы конструкции;

- соответствием механических свойств материала конструкции и испытанных образцов;

- неточностью задания внешней нагрузки;

- долговечностью проектируемой конструкции;

Задачи, решаемые с помощью условия прочности:

а) проверка прочности: заданы все размеры конструкции и вся нагрузка. Необходимо проверить выполняется ли условие прочности;

б) определение минимально-необходимых размеров: заданы основные размеры конструкции и вся нагрузка. Необходимо определить недостающие минимально-необходимые размеры, исходя из выполнения условия прочности;

в) определение грузоподъемности: заданы все размеры конструкции и основная нагрузка. Необходимо определить максимальное значение (грузоподъемность) какой-то нагрузки, исходя из выполнения условия прочности;

1.9 Примеры построения эпюр внутренних усилий

а) статически-определимая плоская рама

Построить эпюры для рамы, показанной на рис. 1.8а

При построение продольную силу считать положительной, если она осуществляет растяжение стержня. Поперечную силу положительной, если она осуществляет поворот элемента стержня по часовой стрелке. Изгибающий момент откладывать со стороны сжатых волокон стержня.

Решение.

Отбрасывая шарнирные опоры, заменяем их действие на действие соответствующих реакций. Для их определения составляем уравнения статического равновесия:

Отсюда при :

Разделяем раму на три участка OA, AB, AC и рассекаем каждый из них в произвольной точке. Составляя уравнения равновесия оставшейся части каждого из участков, определяем внутренние усилия (рис. 1.8а):

На участке OA, рассматривая равновесие нижней части стержня, имеем

(сжаты правые волокна стержня OA).

На участке AB, рассматривая равновесие верхней части стержня, имеем

(сжаты левые волокна стержня AB).

На участке AС, рассматривая равновесие правой части стержня, имеем

(сжаты нижние волокна стержня AC).

По полученным аналитическим выражениям строим эпюры продольных, поперечных сил и изгибающих моментов (рис 1.8б)

Правильность построения эпюр можно проверить с использованием

1) дифференциальных соотношений между внутренними усилиями при изгибе;

2) составления уравнений статического равновесия произвольного участка, вырезанного из рамы;

3) проверки соблюдения граничных условий.

б) криволинейный стержень

Построить эпюры для криволинейного стержня (см. рис. 1.9a)

Для построения эпюр необходимо определить только реакцию . Составляем условие равенства нулю суммы всех моментов относительно точки A:

Рассекаем стержень под произвольным углом (рис.1.9а), отбрасываем левую часть и определяем внутренние усилия из уравнений равновесия в проекциях на нормальное и касательное направления к оси стержня в каждой точке:

Для построения эпюр определяем значения внутренних усилий для разных значений углов:

при

при (чуть левее середины стержня)

при (чуть правее середины стержня)

при

Откладывая полученные значения по перпендикулярно оси стержня (по его радиусу), строим эпюры внутренних усилий (рис. 1.9в)

2. Геометрические характеристики плоских сечений

2.1 Статические моменты и центр тяжести

Рассмотрим плоское сечение и введем прямоугольную декартову систему координат. Для того, чтобы охарактеризовать площадь поперечного сечения введем характеристику . Тогда характеристика нулевого порядка является площадью поперечного сечения и равна (для ).

Статическим моментом сечения площади относительно данной оси называется сумма произведений элементарных площадей на их расстояния до данной оси, определенная для всей площади

, .

Размерность статических моментов ( ). Значение статического момента может быть отрицательным, положительным и равным нулю. Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей называется центром тяжести (в этой точке приложена равнодействующая сил тяжести). В случае если положение центра тяжести известно, то статический момент относительно произвольной оси равен произведению всей площади на расстояние от этой оси до центра тяжести данного сечения.

, .

Центр тяжести произвольного сечения определяется по формулам

, .

Суммирование производится по всем простейшим составным частям сечения , при этом отсутствующие части сечения (например, вырез или дополнения до целого) берутся отрицательными.

Если сечение имеет хотя бы одну ось симметрии, то центр тяжести лежит на данной оси.

Центр тяжести для прямоугольника находится на пересечении его диагоналей, для круга – в его центре, для прямоугольного треугольника – на расстоянии равном 2/3 длины его катетов от каждой из его вершин, образующих острые углы.

Пример.

Для симметричного сечения, состоящего из квадрата со стороной a=10см и круга с диаметром D=10см, определить положение центра тяжести (рис. 2.2).

Решение:

Вводим прямоугольную систему координат , проходящую через центры тяжести отдельных элементов.

Тогда в силу симметрии

Поскольку квадрат со стороной равной диаметру круга имеет большую площадь, то центр тяжести всего сечения, лежащий на оси , оказывается ближе к центру тяжести квадрата.

2.2 Моменты инерции и моменты сопротивления сечения

Осевым моментом инерции сечения относительно данной оси называется сумма произведений элементарных площадей на квадрат расстояний до данной оси, определенная для всей площади : ; по аналогии для оси : . Они являются характеристиками плоского сечения второго порядка для и соответственно.

Полярным моментом инерции сечения относительно данной точки (полюса) называется сумма произведений элементарных площадей на квадрат расстояний до данной точки, определенная по всей площади : .

Размерность осевых и полярного моментов инерции . Их значения могут быть только положительными. Сумма осевых моментов инерции относительно пары двух любых взаимно перпендикулярных осей и , проходящих через данную точку, постоянна и равна полярному моменту инерции относительно центра координат: .

Центробежным моментом инерции относительно двух осей и называется сумма произведений элементарных площадей на расстояния до двух этих осей, определенная для всей площади : . Его значение может быть отрицательным, положительным и равным нулю.

Осевые моменты инерции для простейших сечений:

а) определить осевые моменты инерции для прямоугольника с шириной и высотой .

Решение:

Разбивая сечение на бесконечно-тонкие прямоугольники (рис. 2.3) и интегрируя по высоте сечения, получим ,

по аналогии

б) определить осевые моменты инерции для круга диаметром D.

Пользуясь тем, что для круга , определим :

Разбивая сечение на бесконечно-тонкие кольца (рис. 2.4) и интегрируя от центра круга до наружного радиуса, получим ,

Моментом сопротивления относительно данной оси называется отношение осевого момента инерции для данной оси к максимальному расстоянию точек сечения от данной оси, взятому по модулю: .

2.3 Определение статических моментов и моментов инерции при параллельном переносе осей

Пусть – центральные оси. Определить ,

если известны.

Решение.

Связь между новыми и старыми координатами: , используем определения моментов:

Таким образом, для того чтобы определить новые значения моментов необходимо добавить к их старым значениям поправку на параллельный перенос равную произведению площади поперечного сечения на расстояние между осями в степени соответствующей порядку характеристики (значений ).

Поскольку поправки, определяющие пересчет осевых моментов инерции, всегда положительны, то их значения для центральных осей минимальны.

2.4 Определение моментов инерции при повороте осей

Пусть – произвольные оси и угол 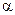>0 – по часовой стрелке. Определить , если известны.

Решение.

Связь между координатами: , используем определения моментов инерции:

Пример.

Для составного сечения (рис.2.2) определить осевые и центробежный моменты инерции и моменты сопротивления .

Решение:

Пользуясь формулами для определения моментов инерции при параллельном переносе осей, суммируя моменты инерции для отдельных элементов сечения, получим

Максимальным расстоянием от оси является ( ), а от оси является , поэтому

2.5 Главные оси и главные моменты инерции.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными. Положение таких осей можно найти в каждой точке плоского сечения. Если начало координат этих осей совпадает с центром тяжести, то такие оси называются главными центральными. Моменты инерции относительно главных центральных осей называются главными (главными центральными) моментами инерции. Формулу для определения положения главных осей инерции по отношению к произвольным осям получим из условия отсутствия центробежного момента инерции, возникающего при повороте осей: .

Подставив найденное значение угла в выражения для осевых моментов инерции при повороте осей, получим формулу для определения главных моментов инерции: .

Главные моменты инерции обладают свойством экстремальности – один из них имеет наибольшее, а другой – наименьшее значение из всех моментов инерции для любой оси, проходящей через данную точку.

Знак ‘+’ берется для наибольшего момента инерции, а знак ‘-’ для наименьшего.

Главные центральные оси инерции обозначаются часто буквами и 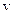, а главные моменты инерции и соответственно.

2.6 Радиусы и эллипс инерции

Радиусом инерции сечения относительно некоторой оси называется величина, определяемая по формуле: .

Радиусы инерции, определенные для главных осей, называются главными радиусами инерции: .

Определив главные радиусы инерции, можно построить главный эллипс инерции:

- провести главные оси

- отложить по оси радиус ,

а по оси 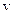радиус по обе стороны от начала координат

- по полученным четырем точкам построить эллипс

Свойства эллипса инерции:

- эллипс инерции ориентирован в направлении распределения материала сечения;

- -расстояние между произвольной осью, проходящей через центр эллипса и осью, параллельной оси и касающейся эллипса является радиусом инерции для данной оси, т.е.

Пример

Положения главных осей для простейших сечений

Стандартные тонкостенные сечения (рис. 2.7) задаются номером (например, двутавр №20 или угольник №12.5/10.0). Геометрические характеристики стандартных тонкостенных профилей определяются по стандарту - сортаменту прокатных профилей по заданному номеру, который определяет высоту профиля или длины его сторон в [см].

2.7 Пример выполнения расчетно-графической работы № 1: Определение геометрических характеристик плоской фигуры

Для заданного несимметричного сварного профиля, состоящего из

2) листа 200x9 мм,

3) швеллера №16,

4) уголка неравнобокого №14/9 (толщина стенки t=8мм)

осуществить

1) определение положения центра тяжести

2) определение положения главных центральных осей

3) построение центрального эллипса инерции

Выполнение данной работы удобно проводить, заполняя следующую таблицу:

Порядок выполнения расчетно-графической работы:

1) Для заданных профилей определяем или берем из сортамента их начальные геометрические характеристики

- для листа

- для швеллера

- для уголка

2) Вводим произвольную начальную систему координат: в данном случае начало координат (точка ) совмещено с левым нижнем концом листа и изображаем в выбранном масштабе составное сечение;

в) Определяем центры тяжести отдельных элементов: исходя из схемы сечения

- для листа

- для швеллера

- для уголка

и заносим их реальные значения в таблицу;

3) Определяем статические моменты элементов сечения , и всего сечения относительно начальной системы координат ;

4) Координаты ЦТ всего сечения:

5) Изображаем на чертеже центр тяжести и центральные оси всего сечения (точка и оси );

6) Определяем координаты центров тяжестей отдельных элементов в системе центральных осей

7) Определяем или берем из сортамента моменты инерции элементов сечения для собственных центральных осей

- для листа ;

- для швеллера

- для уголка ;

Центробежный момент инерции для неравнобокого уголка с толщиной стенки относительно собственных центральных осей определим по формуле:

.

В таблицу записываем , поскольку большая часть площади уголка находится в области, где координаты и точек сечения имеют противоположные знаки.

Осевые моменты инерции записываем в таблицу исходя из реального положения элементов относительно осей .

8) Определяем поправки на параллельный перенос при переходе от собственных центральных осей каждого элемента к общим центральным осям ;

9) Определяем моменты инерции элементов сечения и всего сечения относительно общих центральных осей ;

10) Угол, задающий положение главных центральных осей, определяется по формуле

.

Поскольку угол отрицателен, то откладываем его по часовой стрелке и проводим одну из главных осей .

11) Главные центральные моменты инерции равны

, при этом т.к. , то .

12) Главные центральные радиусы инерции равны

.

Откладывая по оси 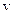радиус , а по оси – радиус , строим эллипс инерции.

3. Одноосное растяжение-сжатие

3.1 Напряжения и деформации при растяжении и сжатии

Принцип Сен-Венана: распределение напряжений существенно зависит от способа приложения внешних сил лишь вблизи места нагружения, а в частях достаточно удаленных от места приложения сил распределение практически зависит только от статического эквивалента этих сил. На рис. 3.1 показан пример систем, имеющих одинаковые главный вектор и главный момент, поэтому деформацию этих систем будем считать одинаковой.

Гипотеза Я Бернулли (гипотеза плоских сечений): поперечные сечения стержня плоские и перпендикулярные его продольной оси до деформации остаются плоскими и перпендикулярными к его оси и после деформации. В таком случае нормальные напряжения можно считать распределенными постоянно по сечению и формула для нормальных напряжений при одноосном растяжении-сжатии принимает вид .

Правило знаков при осевой деформации растягивающая сила (напряжение) – положительна, сжимающая – отрицательна:

Разница между длиной стержня после деформации и начальной длиной стержня называется абсолютной продольной деформацией стержня: .

Отношение абсолютной продольной деформации к начальной длине стержня называется относительной продольной деформацией: .

Отношение абсолютной поперечной деформации стержня к его начальному поперечному размеру называется относительной поперечной деформацией: .