Главные площадки и главные напряжения при объёмном и плоском напряженном состоянии

При повороте элементарного объёма относительно точки М компоненты тензора напряжений (4.1), как показывают формулы (4.5 – 4.8) , изменяются, т.е., их значения зависят от ориентации элементарного объёма в пространстве. Можно указать такую его ориентацию, при которой на наклонной площадке с внешней нормалью ν касательные напряжения τ_y'z' окажутся равными нулю.

Площадки, на которых отсутствуют касательные напряжения, называются главными площадками, а нормальные напряжения, действующие на них, называются главными напряжениями.

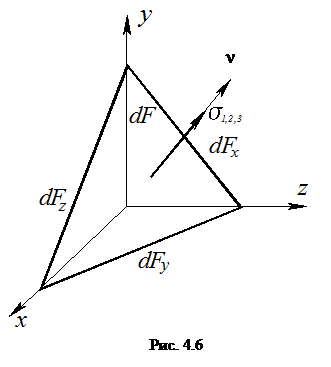Пусть на исходных площадках действуют компоненты тензора напряжений (рис. 4.4). Найдем при этом положение главных площадок и значения главных напряжений на них.

Предположим, что наклонная площадка с нормалью ν является главной с одним нормальным напряжением σ_ν=σ_(i), (i=1_,2,3).

Рассматривая в равновесии выделенную пирамиду, т.е., проектируя все силы на оси координат х, у, z получим

-σ_xdF_{x +} σdFl +τ_yxdF_y+ τ_zxdF_Z = 0

-σ_ydF_{y +} σdFm+τ _xydF_x +τ_zydF_z = 0

-σ_zdF_{z +} σdFn+τ_xzdF_x +τ_yzdF_y = 0:

Разделив последние три равенства на площадь наклонной площадки dF, получим три однородных линейных алгебраических уравнения относительно направляющих косинусов l, m, n:

,

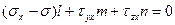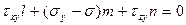, (4.12)

.

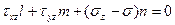Система уравнений не должна иметь нулевое решение в силу того, что сумма квадратов направляющих косинусов равна единице, т. е.:

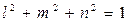(4.13)

Тогда определитель системы уравнений (4.12)

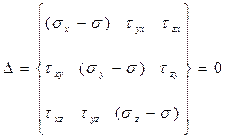(4.14)

Раскрывая определитель системы уравнений (4.14), получим кубическое уравнение относительно нормального напряжения на главной площадке:

σ³–J₁(Т_σ)σ² + J₂(Т_σ)σ – J₃(Т_σ) = 0 (4.15)

Коэффициенты при напряжении σ в уравнении (4.15):

J₁(Т_σ)=σ_x +σ_y +σ_z;

J₂(Т_σ)=σ_xσ_y +σ_yσ_z + σ_zσ_x–τ_xy²-τ_yz²-τ_xy² (4.16)

J₃(Т_σ)=σ_xσ_yσ_z +2τ_xyτ_yzτ_zx–σ_xτ_yz²-σ_yτ_zx²- σ_zτ_xy²

называются первым, вторым и третьим инвариантами напряженного состояния, т.е., величинами, не зависящими от преобразования координат относительно вращения элементарного объёма.

Кубическое уравнение (4.15) имеет три действительных корня, значения, которых расположим в такой последовательности: σ₁≥ σ₂ ≥ σ₂. Напряжения σ₁, σ₂ , σ₃ будут главными, значения их не зависят от операции вращения. Поэтому они будут являться инвариантами а, следовательно, формулы (4.16) можно выразить через главные напряжения:

J₁(Т_σ)=σ₁ +σ₂+σ₃

J₂(Т_σ)=σ₁σ₂+σ₂σ₃+σ₃σ₁ (4.17)

J₃(Т_σ)=σ₁σ₂σ₃

Рассмотрим частный случай, когда σ_x=τ_xy=τ_zx=0 (рис. 4.5). В таком случае инварианты тензора напряжений (4.16) будут равны:

(**)

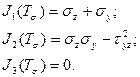Кубическое уравнение (4.15) с учетом (**) преобразуется в квадратное уравнение:

σ² – J₁(Т_σ)σ + J₂(Т_σ)=0 (4.19)

Найдем корни квадратного уравнения (4.19):

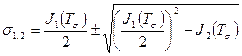(4.20)

После подстановки значений первого и второго инвариантов (4.18) в формулу (4.20) и выполнения элементарных преобразований получим:

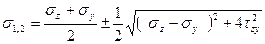(4.21)

Формула (4.20) применяется при определении главных напряжений при плоском напряженном состоянии. В случае если нормальные напряжения σ_y=0, значения главных напряжений

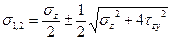(4.22)

Теперь определим положение главных площадок.

Рассмотрим равновесие выделенного элемента (рис.4.7), с действующими на него главными напряжениями σ_1,2 и напряжениями на исходных площадках.

Спроектируем все силы на ось у получим:

σ_1,2dFsinα_1,2 +τ_zydF_z–σ_ydF_y=0

Разделив на dFsinα_1,2 последнее равенство, получим:

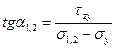
, (4.23)

или в частности, когда σ_y=0:

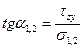(4.24)

Формулы (4.24) и (4.25) используются для определения положения главных площадок при плоском напряженном состоянии.

Положительный угол α_1,2 откладывается от положительного направления оси z против хода часовой стрелки. При этом должно выполняться условие ортогональности главных площадок: сумма модулей углов α₁, α₂ должно равняться 90^об т. е.:

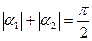
Это указывает на то, что главные площадки, как и исходные площадки взаимно перпендикулярны между собой.