Круг напряжений О. Мора

Соотношения между напряжениями на наклонных и исходных площадках при плоском и объёмном напряженном состояниях можно представить графически с помощью круговой диаграммы. Эта диаграмма была предложена немецким ученым Отто Мором.

В случае плоского напряженного состояния напряжения на наклонных площадках через главные напряжения на основании формул (4.8-4.10) можно представить так (рис.4.12а):

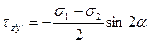(4.57)

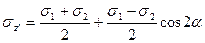(4.56)

Каждой наклонной площадке соответствует своя изображающая точка М окружности с координатами σ_z', τ_y'z'.(рис. 4.12б) При положительном направлении угла α направленном против часовой стрелки ось τ направляется вниз, что согласуется с формулами (4.58): α>0, sin2α>0, τ_y'z'<0 (рис.4.12 в).

Введем обозначения: 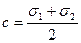, 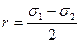. Тогда формулы (4.56) и (4.57) в осях σ и τ будут представлять собой параметрическое уравнение окружности с центром с и радиусом r:

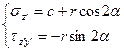(4.58)

Эту окружность называют кругом напряжений О. Мора (рис. 4.12)–(4.13).

Каждой наклонной площадке соответствует своя изображающая точка М окружности с координатами σ_z', τ_y'z'.(рис. 4.12б) При положительном направлении угла α направленном против часовой стрелки ось τ направляется вниз, что согласуется с формулами (4.58): α>0, sin2α>0, τ_y'z'<0 (рис.4.12 в).

Таким образом, чтобы построить круг напряжений следует отложить на оси σ значения главных напряжений σ₁ и σ₂. На отрезке 12, как на диаметре провести окружность. Принимая точку 2 за полюс, провести через нее луч параллельный нормали z', т.е. под углом α к горизонтали с учетом знака, до пересечения с окружностью. Получим изображающую точку М. Координаты этой точки определят в принятой системе осей значения нормальных σ_z' и касательных τ_y'z' напряжений на заданной наклонной площадке.

Рассмотрим построение круга напряжений в случае, когда исходные площадки не являются главными (рис. 4.13а). Для определенности будем считать, что нормальные напряжения σ_z>σ_y >0, касательное напряжение τ_yz>0. Построим изображающую точку М (σ_z, τ_yz), т.е. по напряжениям, дейстующим на площадке с нормалью z. Теперь через изображающую точку М, проведем луч до пересечения с окружностью, получим полюс А. Через полюс А параллельно нормали к наклонной площадке, т.е. под углом α к горизонтали с учетом знака, проведем луч до пересечения с окружностью в точке В, которая является изображающей точкой заданной наклонной площадки. Координаты точки В будут определять значения нормальных σ_z' и касательных напряжений τ_y'z' на этой площадке.

По кругу напряжений можно найти положение главных площадок с напряжениями σ₁ и σ₂. Для этого из полюса А нужно провести лучи через изображающие точки главных площадок 3 и 4, которые укажут на направление нормалей к главным площадкам углами α₁ и α₂=90+α₁. Значение главных напряжений σ₁ и σ₂. будет определяться отрезками О3 и О4 соответственно.

По кругу напряжений можно найти положение главных площадок с напряжениями σ₁ и σ₂. Для этого из полюса А нужно провести лучи через изображающие точки главных площадок 3 и 4, которые укажут на направление нормалей к главным площадкам углами α₁ и α₂=90+α₁. Значение главных напряжений σ₁ и σ₂ будет определяться отрезками О3 и О4 соответственно.

Из рис (4.13) следует, что

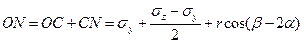
или

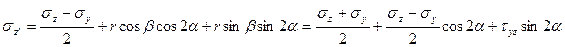
Аналогично доказывается положение:

,

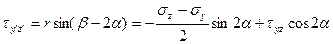что соответсиует исходным формулам, на основании которых строился круг напряжений. Можно получить аналогично и значения главных напряжений:

,

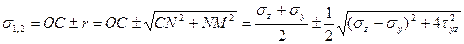Что совпадает с формулой (4.21).

Таким образом все точки круга О. Мора определяют плоское напряженное состояние в точке твердого деформируемого тела.