Какое наибольшее количество различных простых чисел можно выписать в ряд так, чтобы сумма любых четырёх подряд идущих чисел также оказалась простым числом?
Нижегородская (IX открытая) городская математическая олимпиада школьников
НИУ Высшая школа экономики – Нижний Новгород, 11 декабря 2011 года
УСЛОВИЯ И ИДЕИ РЕШЕНИЙ ЗАДАЧ
Класс
1. Вася, когда едет на автобусе, любит играть в игру «100», т.е. из шестизначного номера выданного ему билета составляет числовое выражение, равное 100. При этом можно использовать знаки «+», «-», «:», «´» и скобки, но переставлять цифры местами нельзя. Однажды он получил билет вида 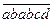 (разные буквы - разные цифры, одинаковые буквы – одинаковые цифры) и сразу составил сотню двумя разными способами:
(разные буквы - разные цифры, одинаковые буквы – одинаковые цифры) и сразу составил сотню двумя разными способами: 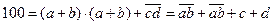 . Какой номер мог быть у него? Предложите также ещё один способ создания 100 из этого номера.
. Какой номер мог быть у него? Предложите также ещё один способ создания 100 из этого номера.
Ответ: 454519; другие способы, например, 4+54+51-9=100, (4+5-4+5)×(1+9)=100, -4+54+5×(1+9)=100, 45×4×5×1:9=100. Решение: Т.к. сумма двух последних цифр 1£c+d£9+8=17, то из второго равенства следует, что 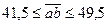 ; тогда a=4. А из первого равенства следует, что a+b£9,т.е. b£5. Переберём все возможные варианты числа
; тогда a=4. А из первого равенства следует, что a+b£9,т.е. b£5. Переберём все возможные варианты числа 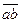 (42, 43 и 45), находя каждый раз из первого равенства число
(42, 43 и 45), находя каждый раз из первого равенства число 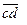 и проверяя его сумму цифр. Получим, что нам подходит только 45, а по нему уже найдём и остальные цифры.
и проверяя его сумму цифр. Получим, что нам подходит только 45, а по нему уже найдём и остальные цифры.
Комментарий: Когда садишься на транспорт, то … сразу получаешь из рук кондуктора задачу, значит, есть время занять мозги делом и потренироваться в устном счёте. Кстати, замечено, что с очень высокой вероятностью на транспорте в руках оказывается хороший билет, из которого можно составить 100. В случае неудачи разрешается использовать факториал, т.к. за счёт 0!=1 и других факториалов появляются дополнительные возможности в создании 100.
2. Василиса Премудрая решила проверить уровень образования Ивана-царевича и задала ему следующую задачу: «На столе лежат числами вверх 9 карточек с числами 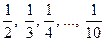 и сундук с приданым, с 10!=1×2×3×…×10 жемчужинами. Можно взять любую карточку и забрать из сундука часть жемчужин, равную написанному на этой карточке числу. Затем можно взять любую оставшуюся на столе карточку и забрать соответствующую часть оставшегося жемчуга из сундука. И сделать так все 9 раз. Как надо действовать, чтобы забрать из сундука максимально возможное количество жемчужин?» Как же надо действовать?
и сундук с приданым, с 10!=1×2×3×…×10 жемчужинами. Можно взять любую карточку и забрать из сундука часть жемчужин, равную написанному на этой карточке числу. Затем можно взять любую оставшуюся на столе карточку и забрать соответствующую часть оставшегося жемчуга из сундука. И сделать так все 9 раз. Как надо действовать, чтобы забрать из сундука максимально возможное количество жемчужин?» Как же надо действовать?
Ответ: порядок выбора карточек не имеет значения. Решение: Рассмотрим количество жемчуга, остающееся в сундуке после каждой операции. Если взяли карточку 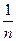 , то в сундуке осталась
, то в сундуке осталась 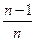 часть имеющегося на данный момент жемчуга. Значит, независимо от порядка выбора карточек в сундуке останется
часть имеющегося на данный момент жемчуга. Значит, независимо от порядка выбора карточек в сундуке останется 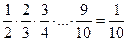 часть всего жемчуга, т.е. 10!:10=9!=362880 жемчужин. Следовательно, из сундука всегда возьмут 10!-9!=3265920 жемчужин. Заметим также, что при любой операции всегда будет оставаться число, кратное натуральным числам, записанным на ещё неиспользованных карточках, т.к. у числа жемчужин в сундуке в изначальном произведении (10!) как множитель будет пропадать только знаменатель взятой карточки и при этом будут появляться новые целые множители. Значит, при любом порядке операций Иван всегда будет брать целое число жемчужин.
часть всего жемчуга, т.е. 10!:10=9!=362880 жемчужин. Следовательно, из сундука всегда возьмут 10!-9!=3265920 жемчужин. Заметим также, что при любой операции всегда будет оставаться число, кратное натуральным числам, записанным на ещё неиспользованных карточках, т.к. у числа жемчужин в сундуке в изначальном произведении (10!) как множитель будет пропадать только знаменатель взятой карточки и при этом будут появляться новые целые множители. Значит, при любом порядке операций Иван всегда будет брать целое число жемчужин.
Комментарий 1: Если Иван-царевич действительно любит Василису Премудрую, то … дело совсем не в приданом:J. Как указал в своём ответе один из школьников – «не в деньгах (жемчужинах) счастье».
Комментарий 2: Если не указано в решении, что на каждом шаге всегда будет взято целое число (см. конец решения), то решение оценивается уже из 6 баллов.
Какое наибольшее количество различных простых чисел можно выписать в ряд так, чтобы сумма любых четырёх подряд идущих чисел также оказалась простым числом?
Ответ: 7, например, подойдёт последовательность 7, 5, 3, 2, 13, 11, 17, где соответствующие суммы по четыре подряд идущих числа равны 17, 23, 29, 43. Доказательство оценки: Сумма четырёх простых чисел будет не меньше 8, значит, чтобы оказаться простой, она должна быть нечётной, следовательно, не может состоять только из нечётных простых чисел, т.е. обязана содержать 2. Но двойка может быть только одна, следовательно, в ряду не более 7 чисел (не более трёх – перед двойкой и не более трёх - после двойки). Если чисел будет ровно 7, то двойка должна стоять на четвёртом месте, что и даёт нам возможность построить нужный пример.
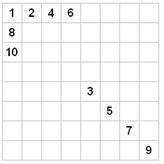 4. На шахматную доску по очереди выставляются ладьи так, что каждая нечётная по очереди выставленная ладья никого не бьёт, а каждая чётная по очереди выставленная ладья бьёт ровно 1 выставленную ранее ладью. Какое наибольшее количество ладей можно поставить на доску по этим правилам?
4. На шахматную доску по очереди выставляются ладьи так, что каждая нечётная по очереди выставленная ладья никого не бьёт, а каждая чётная по очереди выставленная ладья бьёт ровно 1 выставленную ранее ладью. Какое наибольшее количество ладей можно поставить на доску по этим правилам?
Ответ: 10 ладей. Пример см. на рисунке, где число показывает порядковый номер выставляемой ладьи. Доказательство оценки (с помощью теории графов): Рассмотрим двудольный граф, в котором вершины – горизонтали и вертикали, а рёбра – ладьи, стоящие на пересечении горизонтали и вертикали. Тогда постановка нечётной ладьи, бьющей 0 других ладей, создаёт новую компоненту связности из двух вершин, соединённых ребром. Постановка ладьи, бьющей 1 ладью, подсоединяет к какой-нибудь компоненте связности ещё одну висячую вершину. Т.о., в графе количество изолированных вершин (изначально 16) уменьшается на 2+1=3 за каждые два хода. Значит, на доску можно выставить не более [16:3]=5 пар ладей, при этом одна изолированная вершина останется и для следующего хода не будет хватать изолированных вершин. Следовательно, на доску можно поставить не более 5×2=10 ладей. 2-й способ доказательства оценки (без графа): Каждая нечётная по номеру ладья бьёт ровно 4 новые стенки из 32=4×8 стенок на доске (сторон граничных клеток), а каждая чётная ладья бьёт ровно 2 новые стенки, т.к. две стенки ряда (строки-столбца), в котором эта ладья стоит вместе с побитой ею ладьёй, уже были ранее побиты той ладьёй. Значит, каждая пара подряд выставленных ладей бьёт ровно 6 новых стенок, тогда можно выставить ровно [32:6]=5 пар ладей (всего 10 ладей), после чего останется ровно 32-5×6=2 непобитые стенки, которых уже не хватит для появления на доске 11-й ладьи, т.к. ей надо 4 новые стенки.
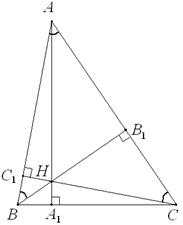 5. Н – ортоцентр (точка пересечения высот) остроугольного треугольника АВС, в котором АН=ВС=a. Найдите площадь четырёхугольника ABHC.
5. Н – ортоцентр (точка пересечения высот) остроугольного треугольника АВС, в котором АН=ВС=a. Найдите площадь четырёхугольника ABHC.
Ответ: a2/2. Решение: Пусть АА1 – высота треугольника АВС (см. рис.), тогда площадь четырёхугольника ABHC равна разности площадей двух из треугольников - АВС и НВС, т.е. ВС×АА1/2-ВС×НА1/2=ВС×АН/2=a2/2.
Комментарий: Вот такая простенькая утешительная геометрия и … снова мало решивших, что грустно.
 9 класс
9 класс
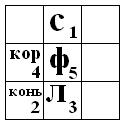
1. Можно ли на шахматную доску выставить по очереди в некотором порядке 5 главных шахматных фигур (ладью, коня, слона, ферзя и короля) так, чтобы каждая фигура в момент постановки на доску била все выставленные до неё фигуры?
Ответ:да, например, как на рисунке, где первой выставленной фигурой будет слон, 2 – конь, 3 – ладья, 4 – король, 5 – ферзь.
2. Докажите, что у многочлена Р(x)=x2011+2x2010+4x2009+8x2008+…+22010x+22011 есть хотя бы один целочисленный корень.
Доказательство: Р(-2)= -22011+22011-22011+22011-…-22011+22011=0, т.к. будет чётное количество (2012) равных по модулю и чередующихся по знаку чисел. Значит, целое число (-2) будет корнем этого многочлена.
3. В прямоугольном треугольнике ABC (ÐC=90°) A1 – точка касания вписанной окружности (с центром I) со стороной BC. Прямая, проходящая через A1 параллельно медиане AM, пересекает AC в точке N. Оказалось, что NI || AB. Найдите остальные углы ∆ABC.
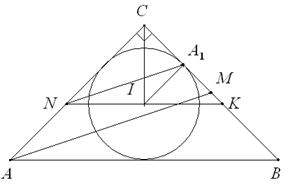 Ответ: ÐА=ÐВ=45°. Доказательство: Пусть NI пересекает BC в точке K. По теореме Фалеса, CA1/A1M=CN/NA=СK/KB. Но CK+KB=2∙CM=2∙(CA1+A1M), значит, CK=2∙CA1 (речь идёт, фактически, о гомотетии с коэффициентом 2 и центром С), т.е. CA1=A1K. Т.к. радиус IA1^CB и CI – биссектриса прямого угла, то ∆CA1I – прямоугольный равнобедренный. Тогда IA1=CA1=A1K, следовательно, ∆CIK – прямоугольный (IK^CI). Но IK||AB, значит, биссектриса CI содержит ещё и высоту DАВС, т.е. DАВС – равнобедренный (AC=BC). Тогда ÐA=ÐB=45°.
Ответ: ÐА=ÐВ=45°. Доказательство: Пусть NI пересекает BC в точке K. По теореме Фалеса, CA1/A1M=CN/NA=СK/KB. Но CK+KB=2∙CM=2∙(CA1+A1M), значит, CK=2∙CA1 (речь идёт, фактически, о гомотетии с коэффициентом 2 и центром С), т.е. CA1=A1K. Т.к. радиус IA1^CB и CI – биссектриса прямого угла, то ∆CA1I – прямоугольный равнобедренный. Тогда IA1=CA1=A1K, следовательно, ∆CIK – прямоугольный (IK^CI). Но IK||AB, значит, биссектриса CI содержит ещё и высоту DАВС, т.е. DАВС – равнобедренный (AC=BC). Тогда ÐA=ÐB=45°.
4. Найдите все пары взаимно простых натуральных чисел a и b, удовлетворяющих равенству (a+b)2=a3+b.
Ответ: a=2, b=1. Решение: Раскроем скобки и перенесём числа в разные стороны двумя способами: a3-a2=b2+2ab-b и b2-b=a3-a2-2ab. Из первого равенства следует, что a3-a2=a2(a-1)Mb, но в силу взаимной простоты a и b получаем, что (a-1)Mb, т.е. либо a=1, либо a-1³b. Из второго равенства следует, что b2-b=b(b-1)Ma, откуда в силу взаимной простоты a и b получаем, что (b-1)Ma, т.е. либо b=1, либо b-1³a. Оба полученных неравенства a-1³b и b-1³a одновременно выполняться не могут, значит, либо a=1, либо b=1. В первом случае при a=1 получаем уравнение b+b2=0, не имеющее решений в натуральных числах. Во втором случае при b=1 после деления на a>0 получаем уравнение a+2=a2, имеющее натуральный корень a=2.
5. Пусть Тk - максимальное количество несоприкасающихся между собой кораблей 1´3 на поле k´k. Докажите, что Т2n=Т2n-1 при любом натуральном n.
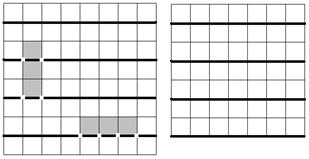
 Доказательство: Очевидно, что при n=1 получаем Т2=Т1=0. Пусть теперь n³2. Рассмотрим на поле 2n´2n все линии сетки с чётными номерами, считая их по порядку сверху поля (всего n линий, см. рис. для случая n=8). Заметим, что любой корабль 1´3 содержит ровно 4 узла на этих линиях - либо все 4 узла на одной, либо по 2 узла на двух подряд идущих из этих линий. При этом на каждой линии будет занято чётное количество узлов, т.е. не более 2n. Тогда на всей доске корабли займут не более n×2n=2n² на этих «чётных» линиях, значит, кораблей будет не более
Доказательство: Очевидно, что при n=1 получаем Т2=Т1=0. Пусть теперь n³2. Рассмотрим на поле 2n´2n все линии сетки с чётными номерами, считая их по порядку сверху поля (всего n линий, см. рис. для случая n=8). Заметим, что любой корабль 1´3 содержит ровно 4 узла на этих линиях - либо все 4 узла на одной, либо по 2 узла на двух подряд идущих из этих линий. При этом на каждой линии будет занято чётное количество узлов, т.е. не более 2n. Тогда на всей доске корабли займут не более n×2n=2n² на этих «чётных» линиях, значит, кораблей будет не более 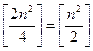 . Аналогично рассматриваем такие же n «чётных» линий на поле (2n-1)´(2n-1) (см. рис. для случая n=7), на которых будет по 2n узлов, и получаем такую же оценку для Т2n-1. Для полей 1´1 и 2´2 очевидно, что Т1=Т2=0, что соответствует полученной оценке. Покажем теперь, что на поле (2n-1)´(2n-1) при n³2 можно выставить
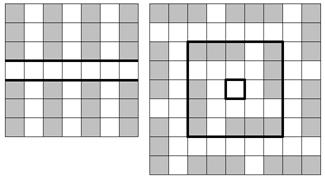
. Аналогично рассматриваем такие же n «чётных» линий на поле (2n-1)´(2n-1) (см. рис. для случая n=7), на которых будет по 2n узлов, и получаем такую же оценку для Т2n-1. Для полей 1´1 и 2´2 очевидно, что Т1=Т2=0, что соответствует полученной оценке. Покажем теперь, что на поле (2n-1)´(2n-1) при n³2 можно выставить 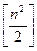 несоприкасающихся кораблей 1´3, а тогда и на поле 2n´2n мы сможем привести точно такую же расстановку кораблей, добавив ещё по одному свободному ряду клеток снизу и справа. 1 случай: 2n-1=4k-1, где k – любое натуральное число, т.е. n=2k - чётное число. Тогда выделяем k горизонтальных полос ширины 3 (см. рис. для случая 2n-1=7), между которыми будет по одному свободному горизонтальному ряду. В каждой такой полосе ставим вертикально ровно 2k кораблей с пропусками между ними одного ряда. Всего расставим
несоприкасающихся кораблей 1´3, а тогда и на поле 2n´2n мы сможем привести точно такую же расстановку кораблей, добавив ещё по одному свободному ряду клеток снизу и справа. 1 случай: 2n-1=4k-1, где k – любое натуральное число, т.е. n=2k - чётное число. Тогда выделяем k горизонтальных полос ширины 3 (см. рис. для случая 2n-1=7), между которыми будет по одному свободному горизонтальному ряду. В каждой такой полосе ставим вертикально ровно 2k кораблей с пропусками между ними одного ряда. Всего расставим 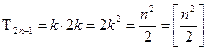 кораблей, что соответствует доказанной выше оценке. 2 случай: 2n-1=4k+1, где k – любое натуральное число, т.е. n=2k+1 - нечётное число. Разобьём наше поле на каёмки ширины 2, вложенные друг в друга (см. рис. для случая 2n-1=9), причём длина внешней стороны каждой каёмки сравнима с 1 по модулю 4, значит, в каждой каёмке с помощью метода «пропеллера» можно по краю, начиная с угла, последовательно выставлять корабли, которые будут занимать клетки циклами по 4 штуки (3 клетки для корабля и 1 пустая клетка), а последняя клетка будет угловой и одновременно начальной клеткой для перпендикулярного ряда кораблей. При этом последняя «каёмка» окажется одиночной клеткой. В результате на корабли уйдут все узлы нашей доски, кроме 4 узлов в центре – вершин центральной клетки-«каёмки», что при подсчёте по 8 узлов на каждый корабль даст нам
кораблей, что соответствует доказанной выше оценке. 2 случай: 2n-1=4k+1, где k – любое натуральное число, т.е. n=2k+1 - нечётное число. Разобьём наше поле на каёмки ширины 2, вложенные друг в друга (см. рис. для случая 2n-1=9), причём длина внешней стороны каждой каёмки сравнима с 1 по модулю 4, значит, в каждой каёмке с помощью метода «пропеллера» можно по краю, начиная с угла, последовательно выставлять корабли, которые будут занимать клетки циклами по 4 штуки (3 клетки для корабля и 1 пустая клетка), а последняя клетка будет угловой и одновременно начальной клеткой для перпендикулярного ряда кораблей. При этом последняя «каёмка» окажется одиночной клеткой. В результате на корабли уйдут все узлы нашей доски, кроме 4 узлов в центре – вершин центральной клетки-«каёмки», что при подсчёте по 8 узлов на каждый корабль даст нам 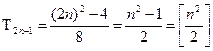 кораблей, что соответствует доказанной выше оценке.
кораблей, что соответствует доказанной выше оценке.
Класс
1. Найдите все квадратные трехчлены ax2+bx+c, корнями которых будут действительные числа a и c.
Ответ: 1). ax2-a2x, где a – любое ненулевое действительное число; 2). x2-(c+1)x+c, где с – любое действительное число; -x2+(c-1)x+c, где c - любое действительное число. Отметим также, что при a=±1 в первом случае будут получаться те же многочлены, что и при с=0 в двух других случаях. Решение:По теореме Виета произведение корней 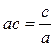 , а сумма корней
, а сумма корней 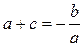 . Рассмотрим 2 случая: с=0 и с¹0. При с=0 из первого уравнения получим, что a – любое ненулевое действительное число; из второго получим, что b= -a2. При с¹0 получим, что a2=1, b= -a2-ac= -1-ac.
. Рассмотрим 2 случая: с=0 и с¹0. При с=0 из первого уравнения получим, что a – любое ненулевое действительное число; из второго получим, что b= -a2. При с¹0 получим, что a2=1, b= -a2-ac= -1-ac.
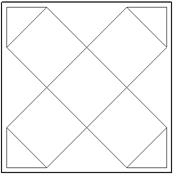 2. Можно ли из квадрата со стороной 3 вырезать многоугольник площади 6, которым можно полностью без наложений и пустот обернуть единичный куб? (классическая фольклорная задача)
2. Можно ли из квадрата со стороной 3 вырезать многоугольник площади 6, которым можно полностью без наложений и пустот обернуть единичный куб? (классическая фольклорная задача)
Ответ: Да, см. рисунок, причём эту фигуру можно вырезать даже из квадрата с меньшей, чем 3, стороной ( 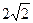 ).
).
3. В треугольнике АВС с ÐВ=30° на средней линии, параллельной стороне АС, взята произвольным образом точка К. Докажите, что КВ<АС.
Доказательство 1: Рассмотрим описанную окружность треугольника АВС с центром О (рис.1), тогда центральный угол ÐАОС=2ÐАВС=60°, значит, DАОС – равносторонний. Отметим точку К’ пересечения луча ВК и отрезка АС, тогда в силу свойств средней линии К’В=2×КВ, но К’В не превосходит диаметра окружности, который равен удвоенной стороне треугольника АОС, т.е. 2×АС, значит, 2×КВ£2×AC, откуда КВ£АС (в частности, возможно и равенство, если К=О и совпадает с одним из концов средней линии).
Доказательство 2: Пусть A’C’ – требуемая средняя линия треугольника АВС (рис.2). Отобразим точку К относительно сторон АВ и СВ, получив точки К1 и К2 соответственно. Тогда ÐК1ВК2=2ÐA’ВC’=60°, ВК1=ВК=ВК2, т.е. DК1ВК2 – равносторонний, значит, КВ=К1К2. Но длина ломаной К1A’C’K2 , во-первых, будет не меньше К1К2, во-вторых, длина этой ломаной равна удвоенной длине отрезка A’C’, т.к. в силу симметрии K1A’=A’K, K2C’=C’K, т.е. длина этой ломаной равна АС=2×A’C’. Значит, КВ=К1К2£2×A’C’=AC.
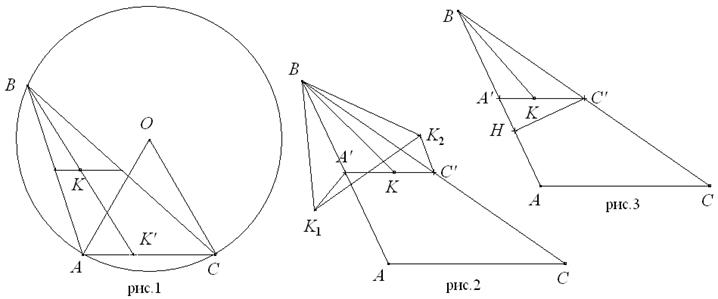 Доказательство 3: Пусть A’C’ – требуемая средняя линия треугольника АВС (рис.3). Т.к. сумма углов A’KB и C’KB равна 180°, то по принципу Дирихле один из них не меньше 90°. С точностью до симметрии можно считать, что Ð C’KB³90°, тогда в D C’KB наибольшей стороной будет C’B. Рассмотрим проекцию Н точки C’ на прямую АВ, тогда, во-первых, в силу свойства наклонной A’C’³НС’, а во-вторых, BC’=2×HC’, т.к. в прямоугольном треугольнике с углом 30° гипотенуза в два раза больше катета, лежащего напротив угла 30°. Кроме того, в силу свойств средней линии АС=2×A’C’. Значит, КВ£BC’=2×HC’£2×A’C’=AC (в частности, возможно и равенство, если К=C’ и A’=Н.)
Доказательство 3: Пусть A’C’ – требуемая средняя линия треугольника АВС (рис.3). Т.к. сумма углов A’KB и C’KB равна 180°, то по принципу Дирихле один из них не меньше 90°. С точностью до симметрии можно считать, что Ð C’KB³90°, тогда в D C’KB наибольшей стороной будет C’B. Рассмотрим проекцию Н точки C’ на прямую АВ, тогда, во-первых, в силу свойства наклонной A’C’³НС’, а во-вторых, BC’=2×HC’, т.к. в прямоугольном треугольнике с углом 30° гипотенуза в два раза больше катета, лежащего напротив угла 30°. Кроме того, в силу свойств средней линии АС=2×A’C’. Значит, КВ£BC’=2×HC’£2×A’C’=AC (в частности, возможно и равенство, если К=C’ и A’=Н.)
Комментарий: Если в работе не было учтено, что на самом деле КВ£АС, то решение оценивалось из 6 баллов.
