Сколько существует различных представлений числа 63000 в виде суммы нескольких (не менее двух) подряд идущих (по возрастанию) целых чисел?
Ответ: 47. Решение: Решим задачу в общем виде для любого натурального n. Возможны два случая, когда в сумме будет нечётное и чётное количество слагаемых, которое обозначим через k, причём для каждого k будет своё представление числа n в виде нужной нам суммы целых чисел. 1). В случае нечётного количества слагаемых сумма всех чисел равна произведению этого количества на среднее число р, которое будет при этом натуральным числом, т.е. n=kp, тогда k может являться любым натуральным нечётным делителем числа n, за исключением 1. Т.е. всего d(n)-1 вариант, где d(n) - количество нечётных натуральных делителей числа n. 2). В случае чётного количества слагаемых (k=2m, где m – натуральное число) сумма всех чисел равна произведению этого количества на среднее число, равное среднему арифметическому двух чисел в середине ряда, т.е. полуцелому числу p/2, где р – нечётное натуральное число. Получаем равенство n=k×p/2=2m×p/2=mp, тогда р может являться любым натуральным нечётным делителем числа n, а по числу р находим число m, затем k=2m. Т.е. всего d(n) вариантов. Таким образом, количество нужных нам представлений равно 2d(n)-1, где d(n) - количество нечётных натуральных делителей числа n. А число d(n) найдём из разложения n на простые множители аналогично формуле 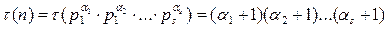 количества всех натуральных делителей числа n, когда мы берём каноническое разложение n на простые множители. Но при нахождении d(n) мы должны учитывать только нечётные простые множители. Т.к. 63000=23×32×53×7, то d(63000)=3×4×2=24 и тогда нужных нам представлений будет 2×24-1=47.
количества всех натуральных делителей числа n, когда мы берём каноническое разложение n на простые множители. Но при нахождении d(n) мы должны учитывать только нечётные простые множители. Т.к. 63000=23×32×53×7, то d(63000)=3×4×2=24 и тогда нужных нам представлений будет 2×24-1=47.
5. Докажите, что система из 3-х уравнений с 9-ю неизвестными 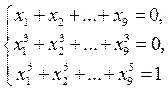 имеет решения в действительных числах.
имеет решения в действительных числах.
Доказательство: Рассмотрим сначала систему уравнений 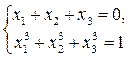 и будем искать частное решение этой системы в следующем виде: x1=x2=a, x3=b. Для переменных a и b мы получаем систему уравнений
и будем искать частное решение этой системы в следующем виде: x1=x2=a, x3=b. Для переменных a и b мы получаем систему уравнений 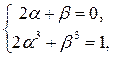 из которой находим b= -2a и -6a3=1. Рассмотрим теперь нашу исходную систему уравнений. Пусть u = (t1, t2, t3) =(a, a, b) - решение предыдущей системы из двух уравнений с тремя неизвестными. Будем искать решение этой новой системы в следующем виде: (x1, x2, x3) = au, (x4, x5, x6)=au, (x7, x8, x9) = bu. Первое уравнение выполняется автоматически, а следующие два уравнения выполняются тогда и только тогда, когда 2a3+b3=0 и 2a5+b5=1, т.е.
из которой находим b= -2a и -6a3=1. Рассмотрим теперь нашу исходную систему уравнений. Пусть u = (t1, t2, t3) =(a, a, b) - решение предыдущей системы из двух уравнений с тремя неизвестными. Будем искать решение этой новой системы в следующем виде: (x1, x2, x3) = au, (x4, x5, x6)=au, (x7, x8, x9) = bu. Первое уравнение выполняется автоматически, а следующие два уравнения выполняются тогда и только тогда, когда 2a3+b3=0 и 2a5+b5=1, т.е. 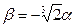 и
и 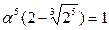 , откуда и найдём a. Таким образом, мы нашли частное решение исходной системы, значит, она имеет решения в действительных числах.
, откуда и найдём a. Таким образом, мы нашли частное решение исходной системы, значит, она имеет решения в действительных числах.
11 класс
1. Какая из сумм больше и на сколько: S(sin) = sin 1° + sin 2° + sin 3° + … + sin 90° или S(cos) = cos 1° + cos 2° + cos 3° + … + cos 90°?
Ответ: сумма синусов больше суммы косинусов на 1. Доказательство: S(sin)-S(cos)= sin 90°- cos 90°=1, т.к. все остальные слагаемые взаимно уничтожатся в силу равенства sina=cos(90°-a).
2. Василиса Премудрая решила проверить уровень образования Ивана-царевича и задала ему следующую задачу: «На столе лежат числами вверх 9 карточек с числами 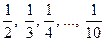 и сундук с приданым, с 10!=1×2×3×…×10 жемчужинами. Можно взять любую карточку и забрать из сундука часть жемчужин, равную написанному на этой карточке числу. Затем можно взять любую оставшуюся на столе карточку и забрать соответствующую часть оставшегося жемчуга из сундука. И сделать так все 9 раз. Как надо действовать, чтобы забрать из сундука максимально возможное количество жемчужин?» Как же надо действовать?
и сундук с приданым, с 10!=1×2×3×…×10 жемчужинами. Можно взять любую карточку и забрать из сундука часть жемчужин, равную написанному на этой карточке числу. Затем можно взять любую оставшуюся на столе карточку и забрать соответствующую часть оставшегося жемчуга из сундука. И сделать так все 9 раз. Как надо действовать, чтобы забрать из сундука максимально возможное количество жемчужин?» Как же надо действовать?
Комментарий: см. решение задачи 8.2.
3. Какое наибольшее количество точек пересечения может быть у графиков трёх функций y=ax2+bx+c, y=bx2+cx+a и y=cx2+ax+b, где a, b и с - попарно различные целые числа?
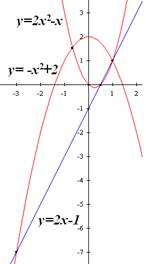 Ответ: 4, например, при a=0, b=2, c= -1, т.к. каждое из трёх получающихся квадратных уравнений 2x-1= -x2+2, 2x2-x=2x-1 и -x2+2=2x2-x имеет по два корня: один общий корень x=1 и три различных – соответственно (–3), 1/2 и (-2/3). Решение: Значения данных функций при х=1 равны a+b+c. Значит, все графики пересекаются в точке с абсциссой 1, и общее число точек пересечения у них не превосходит 4, т.к. каждые два графика пересекаются максимум в двух точках, абсциссы которых являются корнями квадратного уравнения, получающегося приравниванием соответствующих квадратных трехчленов.
Ответ: 4, например, при a=0, b=2, c= -1, т.к. каждое из трёх получающихся квадратных уравнений 2x-1= -x2+2, 2x2-x=2x-1 и -x2+2=2x2-x имеет по два корня: один общий корень x=1 и три различных – соответственно (–3), 1/2 и (-2/3). Решение: Значения данных функций при х=1 равны a+b+c. Значит, все графики пересекаются в точке с абсциссой 1, и общее число точек пересечения у них не превосходит 4, т.к. каждые два графика пересекаются максимум в двух точках, абсциссы которых являются корнями квадратного уравнения, получающегося приравниванием соответствующих квадратных трехчленов.
4.На шахматную доску по очереди выставляются ладьи так, что вторая ладья бьёт ровно 1 выставленную ладью, третья – 2 выставленные ладьи, четвёртая – 0 ладей, пятая – 1, шестая – 2, и т.д. (каждые три следующие выставляемые по очереди ладьи бьют соответственно 0, 1 и 2 выставленные ладьи). Какое наибольшее количество ладей можно поставить на доску по этим правилам?
Ответ: 15 ладей. Пример см. на рисунке, где число показывает порядковый номер выставляемой ладьи. Доказательство оценки (с помощью теории графов): Рассмотрим двудольный граф, в котором вершины – горизонтали и вертикали, а рёбра – ладьи, стоящие на пересечении горизонтали и вертикали. Тогда постановка первых трёх ладей означает, что в графе появилась компонента связности в виде «ёжика» с одной вершиной степени 3 и 3 висячими вершина, т.к. третья по очереди ладья может оказаться только между двумя первыми ладьями. После этого постановка ладьи, бьющей 0 других ладей, создаёт новую компоненту связности из двух вершин, соединённых ребром. Постановка ладьи, бьющей 1 ладью, подсоединяет к какой-нибудь компоненте связности ещё одну висячую вершину. Постановка ладьи, бьющей 2 ладьи либо соединяет две висячие вершины, либо добавляет ещё одну висячую вершину к вершине степени 2. Т.о., в графе после трёх первых ходов есть 12 изолированных вершин, на каждом цикле из трёх следующих ходов количество изолированных вершин уменьшается либо на 2+1=3, либо на 2+1+1=4, значит, мы сможем сделать ещё не более 12:3=4 полных циклов по постановке троек новых ладей и после этого нельзя больше поставить новых ладей. Следовательно, на доску можно выставить не более 5×3=15 ладей. 2-й способ доказательства оценки (без графа): Каждая ладья, номер которой даёт остаток 1 при делении на 3, бьёт ровно 4 новые стенки из 32=4×8 стенок на доске (сторон граничных клеток). Каждая ладья, номер которой даёт остаток 2 при делении на 3, бьёт ровно 2 новые стенки, т.к. две стенки ряда (строки-столбца), в котором эта ладья стоит вместе с побитой ею ладьёй, уже были ранее побиты той ладьёй. Каждая ладья, номер которой делится на 3, бьёт либо 0, либо 2 новые стенки в зависимости от расположения двух ладей, которые она бьёт. Значит, каждая тройка подряд выставленных ладей бьёт не менее 6 новых стенок, тогда можно выставить не более [32:6]=5 троек ладей (всего 15 ладей), после чего останется не более 32-5×6=2 непобитых стенки, которых уже не хватит для появления на доске 16-й ладьи, т.к. ей надо 4 новые стенки.
