Вывод формулы касательных напряжений при кручении круглого вала

Рассмотрим вал круглого поперечного сечения (рис. 7.4) при действии крутящего момента М_z. Образующая DC повернется на угол γ, а соответствующий радиус свободного конца r = OС поперечного сечения повернется на угол φ_l.

Абсолютный угол закручивания это угол поворота поперечного сечения вала относительно своего начального положения. Размерность абсолютного угла закручивания dim φ = рад. Здесь размерность сокращенно обозначена через dim.

Угол поворота произвольного сечения равен φ(z).

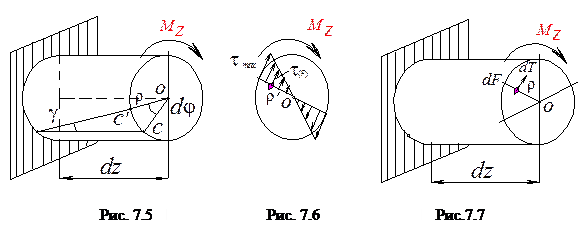
Вырежем из вала элемент малой длины dz радиусом ρ и рассмотрим его деформацию (рис. 7.5). При этом

- с одной стороны длина дуги с˘с΄ = ρdφ;

- c другой - с˘с΄ = γ,dz.

Приравнивая длины с˘с΄, получим такое соотношение: ρdφ = γ,dz. С учетом закона Гука (а) получим такую зависимость:

τ_(ρ) = ρθG, (7.2)

где отношение абсолютного угла закручивания вала к его длине 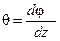- называется относительным углом закручивания. Размерность относительного угла закручивания dim θ = рад/м.

Формула (7.2) показывает, что касательные напряжения τ, действующие в поперечном сечении вала, изменяются по линейному закону (рис 7.6). Максимальные касательные напряжения τ_max действуют в точках у поверхности вала.

Рассмотрим теперь статическую сторону задачи (рис. 7.7). Сумма моментов внутренних сил должна равняться крутящему моменту М_z. Равнодействующая внутренних сил на элементарной площадке dF, отстоящей на расстоянии ρ от центра тяжести поперечного сечения вала

dT = τ_(ρ)dF

Момент этой элементарной силы dT будет равен: dМ_z = dT·ρ

Крутящий момент M_z равен сумме элементарных моментов по всей площади поперечного сечения вала:

М_z = .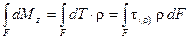

Подставим значения касательных напряжений (7.2) получим: М_z = 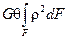. Известно, что 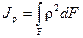- это полярный момент инерции. Отсюда относительный угол закручивания вала

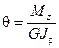(7.3)

GJ_ρ - называют жесткостью вала при кручении, т.е. это произведение модуля сдвига на полярный момент инерции. Крутильная жесткость GJ_ρ характеризует податливость вала при деформации кручения.

Чем больше жесткость GJ_ρ, тем больше вал сопротивляется деформации кручения. Понятно, что жесткость стального вала больше жесткости вала деревянного с равными диаметрами поперечных сечений при действии на них равных крутящих моментов М_z.

Подставляя (7.3) в формулу (7.2), получаем:

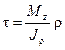(7.4)

Формула (7.4) называется формулой касательных напряжений при кручении вала круглого поперечного сечения.

Для вала сплошного поперечного сечения полярный момент инерции:

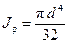(7.5)

В случае кольцевого сечения

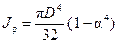, (7.6)

где α = d/D - отношение внутреннего диаметра кольцевого сечения к его наружному диаметру.

Таким образом, формула (7.4) применима для определения касательных напряжений в любой точке валов сплошного и кольцевого поперечных сечений.