Физико-математическая модель движения пузырька в вязкой жидкости с учетом присоединенной массы и силы Бассе
Интерес к данной проблеме связан также с экспериментальными и теоретическими трудностями моделирования движения двухфазной системы ввиду сложности регистрирования быстропротекающих процессов и малых значений динамических параметров, требующих использование чувствительных элементов, и корректного построения моделей с учетом нестационарных слагаемых в уравнении движения, соответственно. В данном разделе мы приведем физико-математическую модель движения пузырька в вязкой жидкости с учетом присоединенной массы и силы Бассе и аналитическое решение для скорости всплытия пузыря для двух случаев:
1. в случае присутствия в жидкости поверхностно–активных веществ (ПАВ) [30]
2. случай без ПАВ, когда необходимо использовать поправку Адамара–Рыбчинского в силе сопротивления
Физико-математическая модель движения пузырька в случае присутствия в жидкости поверхностно–активных веществ (ПАВ)
В отличие от известных работ, посвященных данной проблеме, обзор которых приведен во введении, мы исследуем режим движения пузырька при малых числах Рейнольдса (Re<1).
Математическая модель строится при следующих допущениях:
1. Число Рейнольдса Re<1
2. В жидкости имеются поверхносно–активные вещества (ПАВ), которые препятствуют движению жидкости на поверхности пузыря. Поэтому обтекание пузыря происходит также, как и обтекание твердого шарика.
Введем обозначения:
r – радиус пузыря;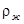 
- плотность жидкости; 
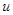- скорость пузыря; t – время; 
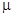- коэффициент динамической вязкости; g – ускорение силы тяжести.
На пузырь действуют силы:
1. инерции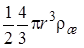 
(масса газа в пузыре мала по сравнению с присоединенной массой жидкости).
2. вязкого сопротивления -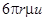 
.
3. ускорение силы тяжести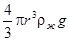 
- сила Архимеда.
4. сила Бассэ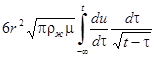 
[30].
Приравнивая эти силы, получаем уравнения движения пузыря (далее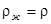 
)
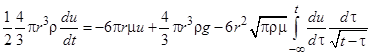. (1)
Поделим это уравнение на присоединенную массу жидкости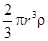 
. Получаем
.
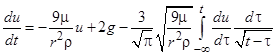Введем характерное время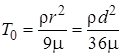 
и безразмерное время 
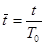. Получим
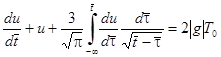, где g<0.
В дальнейшем будем предполагать, что при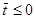 
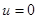[30]. Фактически это означает, что при 
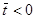пузырек неподвижно закреплен. При этом предположении уравнения движения принимают вид:
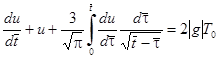. (2)
Так как 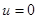при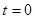 
, второе слагаемое в левой части можно представить в виде 
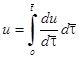и записать уравнение в форме
.
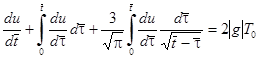Для ускорения пузыря введем обозначение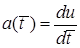 
и получим уравнение
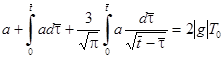. (3)
Последнее уравнение решено операционным методом И.М. Васениным [29]. Полагаем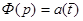 
. При переходе к изображениям воспользуемся теоремой об интегрировании оригинала, согласно которой 
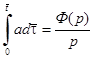и теоремой умножения Бореля
.
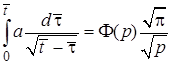(См. [30]).
В результате перехода к изображениям из (3) получим
.
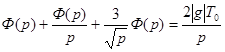Отсюда выражаем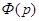 
.
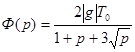С целью нахождения оригинала представим эту формулу в виде
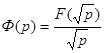, где 
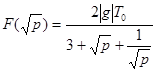. (4)
Согласно [30] оригинал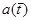 
равен
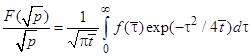, (5)
где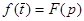 
.
В нашем случае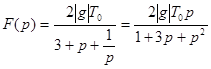 
и оригинал можно вычислить по второй теореме разложения, согласно которой 
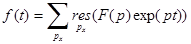, где вычеты берутся по особым точкам функции 
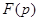[30].
Полагая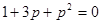 
находим особые точк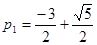и 
и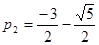 
. Каждая из этих точек представляет собой полюс первого порядка, а функция 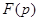является дробно-рациональной функцией вида 
.
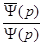Для таких функций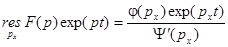 
[30].
Используя эту формулу, находим
,
.
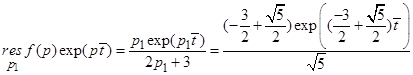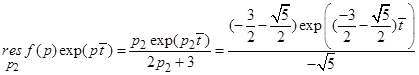Подставляя сумму вычетов в формулу (5) получим
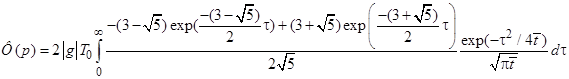(6)
Преобразуем каждый из двух интегралов, входящих в (6)
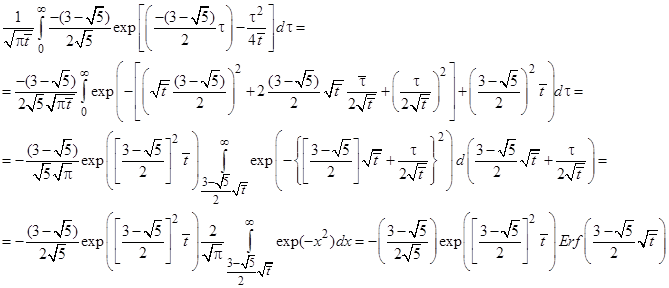Аналогично найдем
.
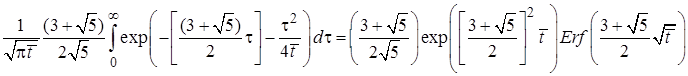Таким образом,
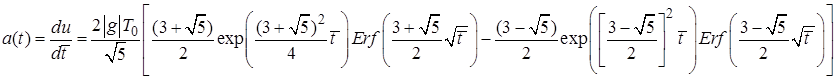(7)
Интегрируя по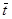 
с начальными условиями 
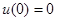получим
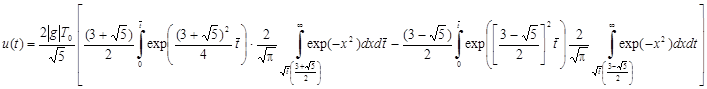(8)
Интегралы вычисляем по частям
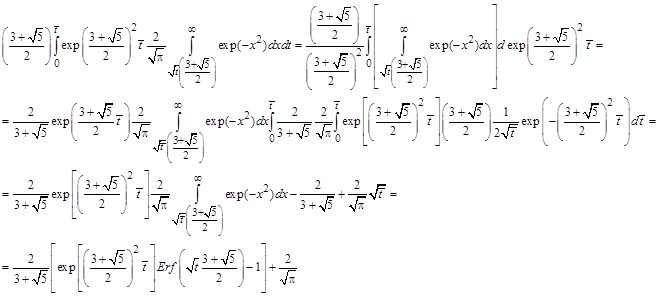Аналогично
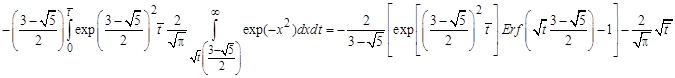
Подставляя интеграл в (8) после приведения подобных найдем
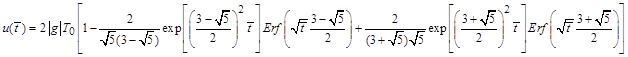
Проверка:
При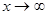 
, 
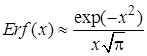и поэтому при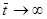 
, 
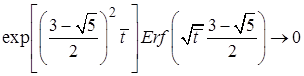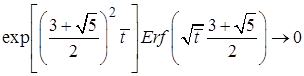, соответственно,
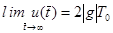. Последний результат есть решение уравнения (8) при 
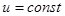, что соответствует выходу на стационарную скорость подъема пузырька.