Оценка влияния эффекта присоединенной массы на движение дисперсной фазы в поле сил тяжести
Присоединённая масса имеет существенное значение при изучении неустановившихся движений тел, полностью погруженных в жидкость, при изучении удара о воду, входа тел в жидкость, качки судов и т.д.
Процессы движения частиц дисперсной фазы (твердых частиц, капель, пузырьков) в поле силы тяжести играют важную роль в природе, в различных технологических процессах. В качестве примеров можно привести закономерности образования атмосферных осадков, седиментации1, барботажа2, распространения облака жидко–капельных аэрозолей и т.д.
Сила, действующая на сферу радиуса R, движущуюся с переменной скоростью в вязкой жидкости (или газе) при Re<1 определяется формулой Буссинеска [1]
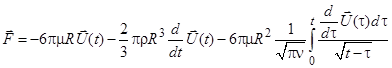 , (1)
, (1)
где 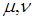 – коэффициенты динамической и кинематической вязкости,
– коэффициенты динамической и кинематической вязкости, 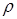 – плотность жидкости. Первое слагаемое силы (1), – сила Стокса, то есть, сила сопротивления; второе слагаемое приводит к понятию присоединенной массы и содержит первую производную от скорости, то есть ускорение. Третье слагаемое – т.н. «наследственная» сила Басе, связанная с предысторией движения. Без учета третьего слагаемого уравнение движения частицы запишется в виде
– плотность жидкости. Первое слагаемое силы (1), – сила Стокса, то есть, сила сопротивления; второе слагаемое приводит к понятию присоединенной массы и содержит первую производную от скорости, то есть ускорение. Третье слагаемое – т.н. «наследственная» сила Басе, связанная с предысторией движения. Без учета третьего слагаемого уравнение движения частицы запишется в виде
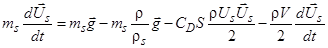 . (2)
. (2)
Здесь индекс s относится к параметрам частиц, V – объем частицы, СD – коэффициент сопротивления сферической частицы. В правой части (2) первый член – сила тяжести, второй – сила Архимеда, третий – сила сопротивления, четвертый – сила, связанная с присоединенной массой. Поскольку в четвертый член входит производная от скорости по времени, можно утверждать, что сила, связанная с присоединенной массой, проявляется в нестационарных процессах и равна нулю в стационарных. В случае Стоксовского режима обтекания частицы (СD=24/Re) сила сопротивления совпадет с силой Стокса в (1). Уравнение (2) перепишем в виде
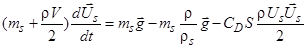 . (3)
. (3)
Сравнивая (3) с классическим уравнением движения
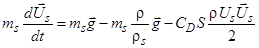 ,
,
видим, что коэффициент перед 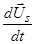 в (3) можно рассматривать как некоторую эффективную массу, которая складывается из массы самой частицы и присоединенной массы, которая равна половине массы жидкости, вытесненной частицей. Ясно, что вклад в движение присоединенной массы будет более значительным при движении пузырька, чем капли или твердой частицы.
в (3) можно рассматривать как некоторую эффективную массу, которая складывается из массы самой частицы и присоединенной массы, которая равна половине массы жидкости, вытесненной частицей. Ясно, что вклад в движение присоединенной массы будет более значительным при движении пузырька, чем капли или твердой частицы.
Разделив (3) на массу частицы 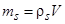 , получим
, получим
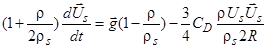 . (4)
. (4)
Введем функцию сопротивления 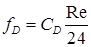 , где
, где 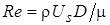 , D=2R – диаметр частицы. Выражая отсюда СD, получим
, D=2R – диаметр частицы. Выражая отсюда СD, получим
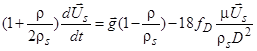 . (5)
. (5)
Обозначим 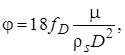 тогда (5) представится в более простом виде
тогда (5) представится в более простом виде
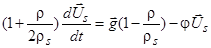 . (6)
. (6)
Будем рассматривать только гравитационное осаждение частицы (всплытие пузырька), т.е. проекцию векторного уравнения (6) на вертикаль. Обозначив
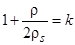 и опуская знаки векторов, получим
и опуская знаки векторов, получим
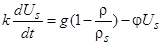 . (7)
. (7)
В случае Стоксовского режима обтекания (Re<1) уравнение (7) имеет аналитическое решение. Следуя [2], получим
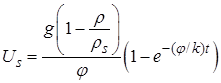 . (8)
. (8)
В общем случае (7) приходится интегрировать численно [2].
В НИИ ПММ ТГУ планируется проведение экспериментального исследование влияния нестационарных эффектов на движение дисперсной фазы (твердых частиц, пузырьков). Предполагаемая схема экспериментальной установки для изучения движения твердых шариков приведена на рис. 1. Для выбора параметров (размеров, вязкости среды и т.п.) установки необходимо предварительно провести серию расчетов движения шариков и пузырьков воздуха в соответствующих средах с использованием либо численного решения (7), либо аналитического решения (8 ).
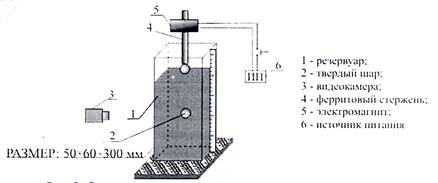
Рис.1. Схема экспериментальной установки.
Формула (8) дает т.н. «предельную скорость» гравитационного осаждения капли или твердой частицы, либо в случае пузырька «предельную скорость» всплытия пузырька. Коэффициент в показателе степени экспоненты 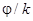 определяет время выхода на стационар этой скорости, а, следовательно, и расстояние по вертикали, которое пройдет за это время шарик либо пузырек.
определяет время выхода на стационар этой скорости, а, следовательно, и расстояние по вертикали, которое пройдет за это время шарик либо пузырек.
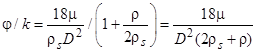 .
.
Для случая пузырька величина члена 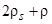 много меньше величины этого члена для случая стального шарика. Отсюда следует, что, чтобы времена выхода на стационар (и соответствующие пройденные расстояния) для обоих случаев были одного порядка, необходимо, чтобы вязкость среды для случая всплытия пузырька была во столько же раз меньше вязкости среды при осаждении стального шарика.
много меньше величины этого члена для случая стального шарика. Отсюда следует, что, чтобы времена выхода на стационар (и соответствующие пройденные расстояния) для обоих случаев были одного порядка, необходимо, чтобы вязкость среды для случая всплытия пузырька была во столько же раз меньше вязкости среды при осаждении стального шарика.
Проведенные оценочные расчеты показали, что использование режима обтекания Стокса (Re<1), при котором справедливо аналитическое решения (8), дает неприемлемо малые для реализации эксперимента времена выхода на стационар (доли секунды), а, главное, малые расстояния (доли миллиметра), через которые устанавливается стационарная скорость.
В связи с этим уравнение (7) интегрировалось численно. На рис. 2-3 приведены некоторые результаты параметрических численных расчетов.
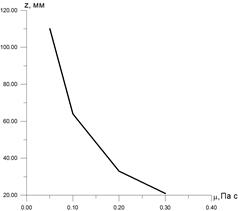 Рис. 3. Зависимость расстояния выхода скорости на стационар от вязкости стального шарика диаметром D=4 мм . Рис. 3. Зависимость расстояния выхода скорости на стационар от вязкости стального шарика диаметром D=4 мм . | 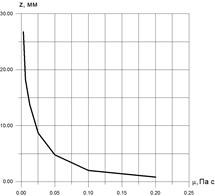 Рис. 4. Зависимость расстояния всплытия пузырька воздуха диаметром D=4 мм до выхода скорости на стационар от вязкости. Рис. 4. Зависимость расстояния всплытия пузырька воздуха диаметром D=4 мм до выхода скорости на стационар от вязкости. |
Из анализа этих рисунков следует, что в случае стального шарика для получения приемлемых размеров рабочей области (60–110 мм) необходимо использовать среду с вязкостью 0.05–0.1 Па с. Такой вязкости можно добиться для водно–глицеринового раствора, изменяя процентное соотношение смеси. В случае пузырька воздуха получаем размер по вертикали 27 мм при вязкости 0.003 Па с. Отсюда следует рекомендация: использовать в качестве рабочей жидкости в этом случае воду, у которой коэффициент динамической вязкости при 20о С 0.001 Па с.
На рис. 4-5 приведено распределение сил сопротивления и сил, связанных с присоединенной массой для случаев падения стального шарика в водно–глицериновом растворе (рис. 4) и всплытия пузырька воздуха (рис. 5) одинаковых размеров.
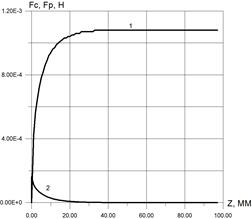 Рис. 4. Сила сопротивления –кривая 1 и сила, связанная с присоединенной массой – 2. Стальной шарик D=4 мм, Рис. 4. Сила сопротивления –кривая 1 и сила, связанная с присоединенной массой – 2. Стальной шарик D=4 мм, 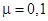 Па с. Па с. | 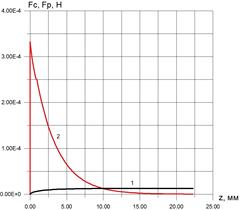 Рис. 5. Сила сопротивления –кривая 1 и сила, связанная с присоединенной массой–2. Пузырек воздуха D=4 мм, Рис. 5. Сила сопротивления –кривая 1 и сила, связанная с присоединенной массой–2. Пузырек воздуха D=4 мм, 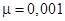 Па с. Па с. |
Из анализа этих рисунков следует, что эффект влияния силы, связанной с присоединенной массой, проявляется больше при движении пузырька.
Здесь следует заметить, что все приведенные оценки достаточно приближенны, поскольку мы пренебрегли членом в уравнении движения, отвечающим за силу Басее. Это, конечно, повлияло на величину ускорения частицы 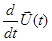 и в результате эффект присоединенной массы искажен.
и в результате эффект присоединенной массы искажен.
В следующих разделах работы приведено продолжение исследований с учетом силы Басе, что значительно сложнее.
