Обнаружение методом непосредственного сравнения

Все критерии качества приводят, по существу, к одному правилу принятия решения. Оно состоит в сравнении отношения правдоподобия Λ с его пороговым значением Λ_п, величина которого определяется выбранным критерием.

Прибор, который использует такое правило, должен иметь сравнивающее (пороговое) устройство, на вход которого поступает величина Λ. Настройка устройства осуществляется в соответствии с выбранным значением Λ_п. На выходе устройства получают решение «Да» (при Λ> Λ_п) или «Нет» (при Λ< Λ_п). однако мы пока еще не знаем, как должна обрабатываться реализация Y, чтобы на вход порогового устройства поступила величина Λ. Эта задача может быть решена, если априорно известны хотя бы некоторые данные о полезном сигнале s(t), вероятностные характеристики помехи n(t) и характер взаимосвязи между полезным сигналом и помехой.

При энергетическом расчете пассивных ОЭП характеристики объекта обнаружения как излучателя обычно известны и задаются в виде математической модели, описывающей изменение интенсивности и спектрального состава излучения во времени и пространстве. Характеристики канала связи (т.е. среды, в которой распространяется излучение от объекта к прибору) также известны. Следовательно, при заданных параметрах системы первичной обработки информации и сканирующего устройства всегда можно рассчитать форму сигнала, который необходимо обнаружить.

Фоновая помеха также задается в виде математической модели, которая описывает фон в виде стационарного случайного яркостного поля и определяет средний уровень яркости (математическое ожидание) и корреляционную функцию или соответствующий ей энергетический спектр.

Закон распределения фоновой помехи и шума ПИ обычно считают нормальным, хотя в отношении некоторых реальных фонов (облачность с разрывами, участок небосвода, включающий линию горизонта и др.) это не вполне соответствует действительности. Необходимо отметить, что при прохождении стационарной и нормально распределенной помехи через линейную систему с постоянными параметрами стационарность процесса и закон распределения помехи не изменяются.

Теперь можно устанавливать связь между реализацией y(t) и отношением правдоподобия Λ. Вначале рассмотрим случай обнаружения при использовании метода однократного отсчета. Суть этого метода состоит в том, что в некоторый момент времени t=t_i берется один – единственный отсчет y(t_i)= y_i реализации y(t), который и поступает на вход порогового устройства. По этому отсчету необходимо принять решение, присутствует объект обнаружения в поле зрения прибора в момент t_i или нет.

Рис.1

На рис.1 пунктиром изображен полезный сигнал на входе порогового устройства. Мгновенное значение сигнала S(t_i)= a_i . поскольку сигнал и помеха аддитивны, то

.

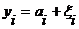В отсутствие полезного сигнала a_i = 0 и y_i = ξ_i . следовательно,

,

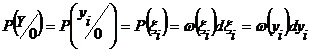где функция 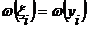представляет собой одномерную плотность вероятности помехи.

Вероятность Р(Y/S) равна вероятности получения случайного значения y_i в реализации, содержащей полезный сигнал и помеху. В силу аддитивности полезного сигнала и помехи эта вероятность совпадает с вероятностью получения случайной величины (y_i –a_i) в реализации, содержащей только помеху. Поэтому

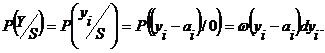
Далее получаем:

.

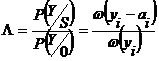Поскольку, помеху можно считать стационарным нормальным случайным процессом с нулевым средним, то y_i и (y_i - a_i) являются центрированными случайными величинами, имеющими также нормальное распределение. Выражение для плотности вероятности нормально распределенной случайной величины Х известно и имеет вид:

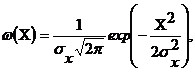
где 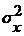- дисперсия случайной величины Х.

В нашем случае, подставляя 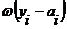и , и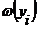меем:

,

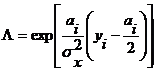где 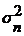- дисперсия помехи.

Из полученного следует, что при известных 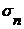и a_i, отношение правдоподобия и отсчет реализации связаны между собой однозначно. Каждому отсчету y_i , взятому из реализации в любой момент времени t_i, соответствует вполне определенное значение Λ, относящееся также к этому моменту времени. Поэтому при обнаружении методом однократного отсчета оказывается достаточным лишь произвести отсчет и передать его в пороговое устройство. Настройка должна производиться не по выбранному значению Λ_п, а по соответствующему ему значению y_п . Найти его можно, положив Λ= Λ_п и y_i= y_п :

.

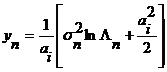При 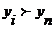выдается решение «Да», при 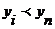- решение «Нет».

Есть два момента, вносящие неопределенность в решение задачи. Во-первых, с какой частотой следует производить отсчеты? Ведь при слишком большом интервале времени между соседними отсчетами полезный сигнал (в силу неизвестности момента его появления) может быть пропущен. Во-вторых (и это также связано с неопределенностью фазы сигнала), как определить значение a_i в момент отсчета? Ведь непосредственное измерение мгновенного значения полезного сигнала по полученному мгновенному значению y_i реализации невозможно из-за наличия помехи.

Ответ на первый вопрос: отсчеты следует производить непрерывно. В этом случае пропуск сигнала исключается. Реализация y(t) непрерывно поступает в пороговое устройство. В те отрезки времени, когда значения реализации превышают порог y_п , выдается решение «Да», в остальное время – «Нет». Таким образом, от метода однократного отсчета мы переходим к методу непосредственного и непрерывного сравнения мгновенных значений полученной реализации с заранее установленным значением порога y_п .

Оптимальная фильтрация

Идеальный приемник обеспечивает максимальную вероятность правильного обнаружения сигнала на фоне помех, его принято называть оптимальным.

Критерием качества приема сигнала может служить отношение правдоподобия. Для случая, когда на вход прибора поступает аддитивная смесь 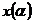полезного сигнала 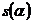и нормальной помехи 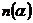, отношение правдоподобия сводится к виду:

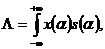(1)

где 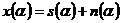; - параметр, по которому оценивается качество приема (время, пространственная координата).

Видно, что максимальное правдоподобие между переданным 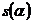и принятым 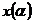сигналами достигается при обеспечении максимума их функции взаимной корреляции, т.е. идеальный приемник должен быть приемником корреляционного типа. Реализация такого приемника связана с большими трудностями. На практике используют другие методы приема сигналов при наличии помех. Наиболее распространенный метод – оптимальная фильтрация.

Если сигнал 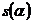заранее известен и его нужно только обнаружить, можно просто определить передаточную функцию оптимального фильтра. Выражение для сигнала на выходе системы с импульсной характеристикой :

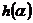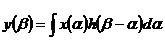(2)

и отношение правдоподобия для оптимальной приемной системы.

Для оптимального приема, т.е. для достижения максимальной идентичности этих двух выражений, необходимо обеспечить идентичность функци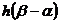й и 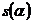. Поскольку аргумент входит в 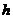и 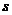с разными знаками, нужна идентичность не просто функци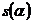й и 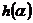, но и идентичность одной из них зеркальному изображению другой, т.е.

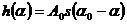. (3)

Величина 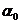учитывает возможный сдвиг начал отсчета функци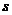й и 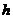и влияет только на фазу выходного сигнала. Для пространственных фильтров, в отличие от временных, часто этот сдвиг можно принять равным нулю, т.е. принять, что выходной и входной сигналы формируются в одной системе координат ( ).

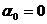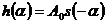, (4)

т.е. импульсная характеристика оптимальной системы обнаружения с точностью до постоянного множителя является зеркальным изображением полезного входного сигнала .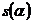

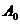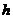Величина является постоянным, не зависящим от , коэффициентом, который учитывает нормировку функций и 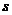, а также различие в их размерностях. Например, 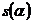характеризует пространственное распределение яркости L на входе объектива, а 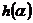- распределение освещенности Е в изображении точечного источника, коэффициент должен учитывать переход от L к Е.

Условие оптимальности фильтра обнаружения можно найти и несколько другим путем. Если представить выходной сигнал как сумму полезного сигнала и шума, т.е. 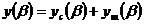, причем

, ,

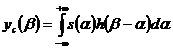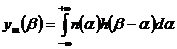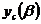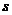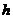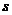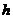то можно заметить, что сигнал является функцией взаимной корреляции и , которая будет максимальна при идентичности и , при .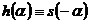

Наедем передаточную функцию оптимального фильтра. Для этого преобразуем по Фурье выражение (3)

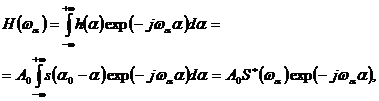(5)

где 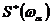- функция комплексно-сопряженная спектру входного сигнала 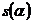; 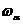- частота; - параметр, по которому ведется анализ (угол, время и т.д.).

При условии равенства модулей 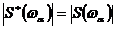имеем

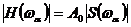, (6)

т.е. амплитудно-частотная характеристика оптимального фильтра при сделанных выше допущениях с точностью до постоянного множителя совпадает с амплитудным спектром входного сигнала.

Такой оптимальный фильтр называют согласованным, поскольку его частотная характеристика целиком определяется спектром сигнала, т.е. должна быть согласована с ним.

Определим выражение для величины сигнала на выходе оптимального фильтра. Применяя обратное преобразование Фурье к спектру сигнала на выходе фильтра, получаем

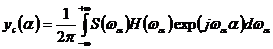(7)

и подставляя сюда (5), получаем

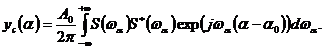
С учетом того, что 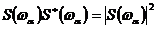, а также пренебрегая фазовым сдвигом выходного сигнала, т.е. принимая 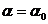, получаем

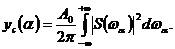(8)

В соответствии с равенством Парсеваля интеграл

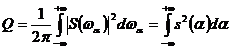(9)

есть полная энергия сигнала, т.е. пиковое значение выходного сигнала равно

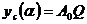. (10)

Когда на выходе системы имеет место гауссовский шум (помеха) со спектральной плотностью на входе 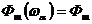, то и на выходе оптимального фильтра он останется гауссовским. Спектр мощности помех на выходе фильтра равен

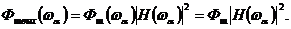(11)

Дисперсия шума на выходе равна

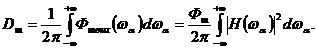(12)

Тогда соотношение сигнал/помеха на выходе оптимального фильтра можно представить в следующем виде

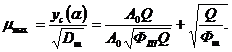(13)

Максимально достижимое отношение сигнал/помеха зависит только от энергии входного сигнала 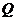и спектральной плотности мощности белого шума 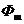на выходе фильтра.

Выражение получено для случая 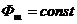, т.е. для шума с равномерной спектральной плотностью в рабочей полосе частот.

Хотя выражения получены для идеализированных оптимальных систем, они весьма полезны и в практике расчета реальных приборов, так как позволяют рассчитать предельно достижимые значения отношений сигнал/помеха, а также установить критерий оптимальности реальных приборов по степени их приближения к оптимальной схеме.

Все выводы действительны и для многомерных функций.

Реализация согласованных фильтров, особенно оптических, затруднена. Поэтому обычным способом оптимальной фильтрации является согласование полосы пропускания фильтра с полосой частот, занимаемой полезным сигналом. Фильтр с оптимальной полосой пропускания 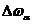, при которой используется большая часть энергии сигнала, называется квазиоптимальным. Известна зависимость между шириной спектра сигнала в виде одиночного импульса 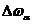и шириной импульса :

.

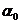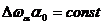При входном сигнале в виде пачки импульсов частотная характеристика согласованного фильтра заметно усложняется. Обычно в этом случае ограничиваются первой полуволной спектра одиночного импульса, из которого составлена пачка, т.е. полосой 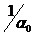. Требуемое число узкополосных фильтров в этом случае равно скважности импульсов.

При переходе от одиночного импульсного сигнала к сигналу в виде пачки импульсов той же формы выигрыш в отношении сигнал/помеха составляет столько раз, сколько одиночных импульсов содержится в пачке.

Таким образом, оптимальным фильтром называют такую линейную систему обнаружения сигнала с полностью известными параметрами, которая осуществляет обнаружение наилучшим образом, т.е. обеспечивает максимум отношения сигнала к шуму на выходе при заданных вероятностях обнаружения и ложной тревоги.

Математическое выражение для коэффициента передачи оптимального фильтра может быть настолько сложным, что высказать даже ориентировочные предположения о схеме фильтра крайне трудно.

Характеристикой качества любого линейного фильтра может служить величина:

,

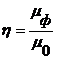показывает во сколько раз отношение сигнал/шум 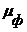на выходе этого фильтра меньше отношения сигнал/шум 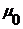на выходе оптимального фильтра.

Тема 16. Электронно-оптические преобразователи.Структура ОЭС с электронно-оптическим преобразователем, принцип работы ЭОП, основные характеристики и параметры ЭОП, формирование информационных сигналов. Приборы ночного видения.