Шумы фотоприемного устройства и точки их приложения

Минимальный поток излучения, который может быть обнаружен фотоприемником, ограничивается случайными флуктуациями, называемыми шумами. Шумы, действующие в фотоприемном тракте, возникают под действием случайных внешних и внутренних процессов, воздействующих на фотоприемное устройство. В силу случайного характера шумовых процессов предсказать величину шумов в заданный момент времени невозможно, поэтому для их оценки используют статистические методы, на основе которых величину флуктуаций значений амплитуды шумовых сигналов оценивают дисперсией u² , то есть средним значением квадрата отклонения случайной величины u от ее среднего значения за временной интервал t: .

Обычно приемники излучения характеризуют среднеквадратичным значением флуктуаций напряжения на нагрузке, либо тока на его выходе в заданной полосе частот, а интенсивность шумов действующих в приемно-передающем тракте оценивают величиной их спектральной плотности, которая характеризуется частью средней мощности S_T(w) случайных флуктуаций приходящейся на частотный диапазон от w до (w+dw).

Различают внешние и внутренние шумы устранимые и неустранимые. По физической природе внешние шумы представляют собой флуктуации потока излучения приходящего на фотодетектор. Эти флуктуации вызваны рядом причин, к которым относятся: модуляция неравномерного фона анализаторами изображения, статистический характер потока излучения (фотонные шумы), случайный характер радиационного и конвективного энергетического теплообмена между фотоприемником и окружающей средой (радиационные шумы). Внутренние шумы - это шумы, возникающие в самом фотоприемном устройстве и в силу того, что они зависят не только от свойств фотодетекторов, но и от схемы их включения и условий работы их подразделяют на собственные шумы фотодетекторов и шумы схемы.

К основным видам собственных шумов относят шум дробового эффекта, тепловой шум, генерационно-рекомбинационный шум, избыточный шум.

Дробовый шум фототока. Известно, что процесс преобразования потока фотонов в фотодетекторе носит дискретный характер, поэтому результатом преобразования является поток дискретных носителей заряда - электронов создающий ток во внешней цепи. Каждый из созданных электронов во внешней цепи вызывает импульс тока, обусловленный зарядом электрона и скоростью его движения , где d -расстояние между электродами преобразователя.

Допустим, что на интервале времени 0-T процесс преобразования описывается функцией u(t), преобразование Фурье которой имеет вид . Мгновенное значение мощности процесса u(t) равно u²(t). Полагая, что функция действует u(t) на ограниченном интервале времени (t₂-t₁) = T, найдем среднее значение мощности этого процесса в виде . Обозначив через S(w), найдем значение средней мощности в виде , где S(w) определяет спектральную плотность процесса в диапазоне частот от w до ( w+dw). Так как S(w)dw=S(f)df, то

(1)

и спектральная плотность мощности фототока, создаваемая одним импульсом тока, равна , так как при малых временах t_a=T жизни электрона wt_a<<1.

Допустим, что на интервале T процесс фотодетектирования определяется функцией u(t) и формируется случайной последовательностью импульсов тока, спектральная плотность мощности которого равна . С учетом полученной ранее формулы спектральную плотность мощности фототока можно представить формулой S(f)=2pS(w), а полученное ранее выражение (1) в виде . Среднее число зарядов на интервале T определяется средней скоростью электронной эмиссии и длительностью интервала T, и равно . Следовательно, спектральная плотность мощности фототока будет равна , а отражающее ее среднеквадратичное значение амплитуды интенсивность дробовых шумов примет вид .

Входящее в эту формулу значение отражает среднее значение суммарного тока фотодетектора вызванного потоком излучения и термотоком, а задается эквивалентной полосой пропускания частот фотоприемника , где k(f) - коэффициент передачи фотоприемного тракта, а K₀ его максимальное значение на частоте f=0.

Тепловой шум. Тепловой шум обусловлен хаотическим тепловым движением носителей заряда в металлах и полупроводниках, иногда его называют шумом Джонсона. Шум не зависит от приложенного к элементу напряжения, а интенсивность шума оценивается по формуле Найквиста среднеквадратичным значением напряжения по формуле , где k –постоянная Больцмана, T- абсолютная температура проводника (K⁰), R_Н – сопротивление проводника.

Генерационно-рекомбинационный шум. В процессе преобразования потока излучения в электрический сигнал в виде потока носителей заряда в полупроводниках возникают флуктуации скоростей генерации и рекомбинации свободных носителей заряда, что влечет за собой флуктуации концентрации свободных носителей и, как следствие флуктуации проводимости. По мере роста частоты спектральная плотность шума падает, а с ростом напряжения питания интенсивность шума нарастает.

Избыточный шум. Избыточный шум объединяет несколько видов шумов с интенсивностью обратно пропорциональной частоте (º1/f) и возникающих только при протекании тока через приемник. Эти шумы зависят от типа фотоприемника, основная интенсивность лежит в области низких частот (сотни Гц).

Дробовой и тепловой шумы являются широкополосными шумами, их интенсивность слабо зависит от частоты и спектральную плотность шумов можно считать равномерной по частотному спектру. Такие шумы, обычно, принято называть белыми шумами.

Среди внешних шумов существенную роль играет радиационный шум. Этот шум возникает вследствие флуктуаций числа фотонов фона и источника излучения. На выходе фотоприемника эта составляющая шумов оценивается по формуле и имеет свойства белого шума.

В общем случае все источники шумов, возникающие в фотоприемном устройстве, считаются статистически независимыми и, по этой причине, суммарное значение среднеквадратического значения напряжения шума на выходе фотоприемника равно .

Точки приложения шумов

Действие шумов на фотоприемное устройство складывается из действия внешних и внутренних шумов, существенно различающихся по своей природе. По физической природе внешние шумы образуются вследствие флуктуаций потока излучения приходящего на фотоприемное устройство. Составляющими этих шумов являются модуляция неравномерного фона анализаторами изображения, статистический характер потока излучения, случайный характер радиационного и конвективного теплообмена между фотоприемником и окружающей средой , которые при токовой интегральной чувствительности фотодетектора , зависящая от спектрального состава излучения, создают на выходе фотоприемного устройства шум со спектральной плотностью мощности равной .

Рис.2. Точки приложения шумов в ФПУ

Показанная на рис.2 схема отражает основные точки приложения внутренних шумов действующих в фотоприемном устройстве.

Методы описания шума

Процесс регистрации сигнала при наличии шумов требует предварительного знания отличительных признаков сигнала и шума. Использование этих признаков позволяет решить задачу обнаружения сигнала и шума.

Шум представляет собой случайную функцию, которая может приносить тот или иной вид – какой заранее неизвестно.

Конкретный вид называется реализацией случайной функции.

Аргументом случайной функции может быть не только время, но и пространственные координаты.

Статистические свойства шума в общем случае описываются многомерными законами распределения.

Имеем случайную функцию U(χ) и ее две конкретные реализации U₁(χ) и U₂(χ), где χ – обобщенная координата.

Рис. 1.Реализации случайной функции

Если зафиксировать значение аргумента χ, то случайная функция при этом аргументе будет представлять собой случайную величину, которую называют сечением случайной функции. Эта величина U может принимать любые значения.

Предполагая, что вероятность попадания случайной величины U внутнри малого интервала dU пропорциональна интервалу, можно охарактеризовать ее этой вероятностью:

,

или значением коэффициента пропорциональности – функцией

,

которую называют плотностью распределения вероятностей случайной величины U, или одномерным законом распределения вероятностей случайной функции.

Условие нормировки для непрерывной случайной величины U

,

вероятность пребывания ее в этом промежутке равна единице.

Законы распределения большей частью неизвестны, но при дополнительных условиях они хорошо аппроксимируются нормальным или гауссовским законами распределения.

Наиболее доступными и достаточными для описания вероятностных характеристик случайных функций являются их числовые параметры – математическое ожидание, дисперсия и корреляционная функция.

Математическое ожидание случайной функции U(χ) представляет собой некоторую среднюю функцию, вокруг которой различным образом располагаются конкретные реализации случайной функции.

При каждом значении аргумента средняя функция равна среднему значению (математическому ожиданию) соответствующего сечения случайной функции.

Среднее значение сечения случайной функции Ū равно сумме произведений всех возможных значений случайной величины на вероятность этих значений:

.

При экспериментальных исследованиях используется способ усреднения по аргументу χ

,

где U(χ) – одна из реализаций в интервале ±х.

Среднее значение для каждой реализации будет своё.

Для случайных функций, называемых эргодическими среднее по аргументу равно среднему по множеству наблюдений , вероятность равна единице.

Дисперсия случайной функции U(χ) представляет собой некоторую неслучайную функцию, значение которой для каждого χ равно дисперсии сечения случайной функции.

- дисперсия случайной функции.

Дисперсию случайной функции можно найти, вычисляя для различных χ.

- среднеквадратическое отклонение случайной величины.

Для стационарной функции дисперсия, вычисленная по множеству реализаций, постоянна .

Дисперсия случайной функции может вычисляться как среднее по аргументу χ:

.

Математическое ожидание и дисперсия не дают полного представления о случайной функции.

Рассмотрим два соседних сечения случайной функции U₁ = U(χ₁) и U₂ = U(χ₂). При близких значениях χ₁ и χ₂ величины U₁ и U₂ связаны тесной зависимостью. При увеличении же интервала между сечениями χ₁ и χ₂ зависимость между U₁ и U₂ должна ослабевать.

Степень зависимости характеризуется некоторой функцией двух аргументов χ₁ и χ₂ – корреляционной функцией, которая определяется как математическое ожидание произведения двух центрированных случайных величин U₁ – Ū₁ и U₂ – Ū₂

.

Для стационарного случайного процесса корреляционная функция не зависит от того, где на оси χ располагаются два сечения U(χ₁) и U(χ₂), а зависит только от разности

Для эргодического случайного процесса функция корреляции может быть вычислена как среднее по аргументу.

Случайная функция называется эргодической, если ее среднее значение, дисперсия и корреляционная функция, вычисленные по нескольким реализациям, совпадают со средними значениями, вычисленными для одной реализации при достаточно большом значении временного или пространственного интервала усреднения.

Общий суммарный шум

Прежде всего, необходимо рассмотреть условия работы прибора и определить виды шумов, которые необходимо учитывать при анализе и расчете.

Одним из важных обстоятельств является распределение спектральной плотности шума по частотам, так как в различных областях спектра электрических сигналов определяющими являются шумы различной природы. Например, для фоторезисторов на самых низких частотах (150-200 Гц) преобладает токовый шум со спектром , на промежуточных частотах основным является генерационно – рекомбинационный шум, а на сравнительно высоких частотах спектральная плотность шума определяется шумом Джонсона (тепловым).

Виды шумов приемников излучения:

1. Тепловой шум возникает вследствие хаотического теплового движения свободных электронов, в результате чего число электронов, движущихся вдоль проводника в одном направлении, не равно числу электронов, движущихся в противоположном направлении (в любой момент времени).

2. Генерационно-рекомбинационный шум обусловлен случайным характером генерации электронов за счет теплового возбуждения кристаллической решетки полупроводника, а также случайным характером рекомбинации этих электронов, т.е. флуктуацией числа и времени жизни носителей.

3. Токовой шум обусловлен случайными изменениями сопротивления полупроводника вследствие различных контактных и поверхностных явлений.

4. Радиационный шум возникает вследствие флуктуаций числа фотонов, эмитируемых источниками излучения и падающих за определенный промежуток времени на приемник; источниками излучения могут быть теплоизлучающие цели, окружающие их фоны и предметы, находящиеся в непосредственной близости от приемника.

5. Температурный шум определяется случайными колебаниями температуры приемника относительно некоторого среднего значения.

6. Дробовой шум возникает вследствие флуктуации во времени потока дискретных частиц, образующих электрический ток.

7. Шум мерцания обусловлен случайными изменениями эмиссии фотокатода.

Средние квадратические значения напряжения шумов рассчитывают по следующим формулам:

; ;

;

; ;

; ,

где - постоянная Больцмана, равная ; - температура приемника, К; - темновое сопротивление приемника, Ом; - рабочий интервал частот, Гц; - напряжение источника питания приемника, В; - сопротивление нагрузки, Ом; - время жизни носителей, с; - концентрация носителей, ; - объем чувствительного материала приемника, ; 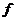- частота модуляции лучистого потока, Гц; - среднее значение тока, А; А – постоянный коэффициент; и - коэффициент излучения и площадь излучения цели (объекта); - площадь чувствительной площадки приемника, ; - заряд электрона, ; - постоянная, характеризующая природу фотокатода.

Тема 14. Энергетический расчет ОЭС. Основные энергетические характеристики излучения: поток излучения, яркость и сила света, энергетическая светимость и освещенность. Оценка освещенности входного зрачка ОЭП активного действия, излучателя с тепловым и лазерным источником. Оценка освещенности входного зрачка создаваемая диффузно - рассеивающим объектом. Расчет дальности действия ОЭС.