Моделирование. Информационные модели.
Моделирование. Информационные модели.
Системы. Общие понятия
Понятие системы является одним из важнейших во многих отраслях науки и техники. Единого общепринятого определения системы не существует, но в самом широком смысле под системой понимают множество, элементы которого закономерно связаны между собой. Элементами множества могут при этом являться те или иные предметы, явления, процессы, знания и многое другое. Соответственно можно говорить о системе уравнений, об оптической системе, о системе передачи данных и т.п.
Таким образом, если событие X в элементе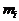 
множества M определенным образом приводит вероятностным образом к событиям в других элементах 
, 
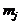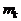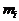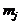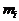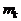, и т.д., то можно утверждать, что между элементами и , и и т.д. существует определенная связь. Вот такие множества, в которых наблюдаются определенные взаимосвязи и носят название систем. Понятие системы противопоставляется понятию хаоса. Хаотически можно назвать такое множество элементов 
, 
, 
, ..., 
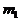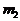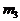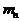, в котором при некотором событии X в элементе 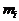могут произойти всевозможные события в остальных элементах.
Существует разновидность систем, у которых событие X в каком-либо элементе однозначно определяет события в других элементах. В таких системах связи между элементами и событиями в них строго и однозначно определены, детерминированы и подобные системы называют детерминированными. Примером таких систем может служить ЭВМ, телевизор и т.п.
В системах иного вида связи между элементами и событиями в них носят вероятностный характер и подобные системы называют вероятностными или стохастическими.
Следует отметить, что строго говоря детерминированных систем вообще не существует, так как даже самая простая система не дает абсолютной гарантии взаимосвязи событий. Поэтому разделение систем на детерминированные и стохастические условно, и строго говоря, все системы стохастические, а детерминированными мы называем те стохастические системы, у которых вероятность ожидаемого события практически равна единице.
Важнейшим свойством системы, являющимся убедительным проявлением закона диалектики о переходе количества в качество, является неаддитивность свойств совокупности элементов, образующих систему, свойство ее нелинейности. Действительно, свойства автомобиля как системы, способной к самостоятельному движению, никак не могут быть получены путем суммирования отдельно взятых свойств ее элементов: колес, топлива, педалей и т.д.
Этот принцип появления в системе свойств, не выводимых из наблюдаемых свойств элементов и связей между ними называют принципом эмерджентности (англ. emergent - неожиданно появляющийся). Этот принцип особенно заметно проявляется в сложных больших системах.
Обязательными компонентами любой системы всегда являются элементы и связи между этими элементами, что в совокупности определяет структуру системы. Структура - это определенная взаимосвязь, взаиморасположение составных частей, характеризующее строение системы.
В общем, любой элемент системы может быть расчленен на более мелкие составляющие (вплоть до молекул). Однако, на практике условились называть элементом системы такую ее часть, которая выполняет определенную специфическую функцию. Следовательно, процесс деления системы на элементы и само понятие элемента условно и весьма относительно.
Элементы любых реальных систем являются некими физическими объектами, которые можно характеризовать их составом, габаритами и т.д. Однако с точки зрения их поведения в системе в большинстве случаев можно отвлечься от их физических свойств и характеризовать их только возможностью образовывать те или иные виды связей: вещественных, энергетических и информационных - с другими элементами и с внешней по отношению к системе средой.
Необходимо отметить, что все три вида связей существуют всегда неотделимо друг от друга, но в зависимости от того, какой вид связи является определяющим, данную связь можно отнести к одному из перечисленных видов.
Следовательно, важнейшей характеристикой элемента в системе является его способность к установлению связей, т.е. к порождению (генерации) или восприятию (поглощению) связей.
Таким образом, при исследовании, анализе и моделировании систем пользуются идеализированными моделями элементов и систем.
Идеализированный элемент представляет некий абстрактный элемент, у которого отсутствуют любые физические свойства кроме способности к реализации связей с другими элементами.
Совокупность идеализированных элементов, объединенных необходимыми связями, образует идеализированную модель системы.
Как указывалось выше, любой элемент можно рассматривать как совокупность более мелких элементов, то есть как систему.
Таким образом, любая система имеет, как правило, иерархическую структуру, то есть многоуровневую структуру. При решении практических задач достаточным оказывается выделение ограниченного числа ступеней иерархии. При этом системы низшего уровня называют подсистемами систем высокого уровня, которые в свою очередь являются подсистемами систем еще более высокого уровня и т.д., вплоть до так называемой суперсистемы, находящейся на верхней ступени иерархической структуры.
Простой называют такую систему, работу которой можно исследовать как нечто целое без разбиения ее на подсистемы.
Большими и сложными называют системы с разветвленной структурой и значительным количеством взаимосвязанных и взаимодействующих элементов.
По характеру перехода из одного состояния в другое системы делят на статические и динамические. Динамическими называют такие системы, переход которых в новое состояние не может совершиться мгновенно, а происходит в результате некоторого процесса, растянутого во времени. Строго говоря, все реальные системы являются динамическими, однако, если временем перехода можно пренебречь, то говорят о статических системах.
Работа любой системы происходит в некоторой окружающей ее внешней среде, не входящей в систему, но определенным образом взаимодействующую с ней. В принципе внешняя среда всегда оказывает влияние на любые системы. Однако в зависимости от степени и практической значимости этого влияния системы подразделяются на открытые и закрытые.
Процессы в открытых системах определяются влиянием внешней среды и сами оказывают на нее воздействие. Следовательно, их функционирование определяется как внутренней, так и внешней информацией, поступающей на входы системы.
Закрытые или замкнутые системы - это системы, в процессе функционирования которых используется только та информация, которая вырабатывается внутри самой системы, так что все взаимодействия между элементами системы определяются процессами, протекающими внутри самой системы.
При изучении явлений и процессов в любых системах можно, очевидно, применять два подхода. Один из них - локальный - заключается в изучении структуры и функциональных особенностей автономных отдельно взятых элементов системы. Другой - системный подход - представляет исследование способов организации элементов системы в единое целое и взаимного воздействия системы, ее подсистем и элементов друг на друга.
Состояние любой реальной системы в каждый данный момент времени можно описать с помощью некоторого множества характеризующих систему величин - параметров. Количество параметров даже для относительно простой системы может быть очень большим, поэтому практически для описания систем, используют лишь наиболее существенные, характерные для нее параметры, соответствующие конкретным целям изучения.
Так, при исследовании здоровья человека с точки зрения освобождения его от работы принимают во внимание температуру и кровяное давление, и при проверки подготовки абитуриента интересуются совсем иными параметрами: грамотностью, умением решать задачи.
Для описания состояния и движения системы можно применять различные способы, но в технике особенно широкое применение находит математическое описание, которое для наглядности часто интерпретируют графиками, отображающими протекание тех или иных процессов. Наиболее удобным из них является метод описания состояния систем и их движения в пространстве состояний или фазовом пространстве.
Пространством состояний системы называется пространство, каждой точке которого однозначно соответствует определенное состояние рассматриваемой динамической системы, а каждому процессу изменения состояний системы соответствует определенная траектория перемещения изображающей точки в пространстве.
В этом методе используется фазовое пространство (n-мерное Евклидово пространство), по осям которого откладываются значения всех n обобщенных координат рассматриваемой динамической системы. При этом взаимно однозначное соответствие между состояниями системы и точками фазового пространства достигается выбором числа измерений n-мерного пространства, равного числу обобщенных координат рассматриваемой системы.
Параметры некоторой системы можно обозначить символами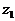 
, 
, 
,..., 
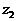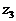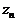, которые можно рассматривать как компоненты вектора Z n-мерного пространства
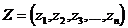. (5.1)
Параметры 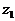, , 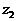,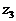..., 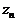называют фазовыми координатами системы, а состояние (фазу) системы изобразим точкой Z в фазовом пространстве.
В реальных условиях работы системы ее параметры (фазовые координаты), как правило, могут меняться лишь в некоторых ограниченных пределах. Область фазового пространства, за пределы которой не может выходить изображающая точка, называют областью допустимых состояний системы. При исследовании и проектировании систем всегда исходят из того, что система остается в пределах ее допустимых значений. Если изображающая точка выйдет за пределы этой области, то это грозит разрушением системы.
Фактически в нормальных условиях эксплуатации параметры системы изменяются в значительно более узких пределах. И совокупность изображающих их точек образует область рабочих состояний. Геометрически область рабочих состояний всегда должна находиться внутри области допустимых значений.
Переход системы из одного состояния в другое будет характеризоваться фазовыми траекториями.
А под движением системы понимают некую последовательность изменения ее состояний.
Табл. 1.1
| k | |||||||
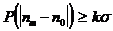 | 0,32 | 0,046 | 0,27·10-3 | 6,3·10-5 | 5,7·10-7 | 2,0·10-9 | 2,5·10-12 |
Таблица 1.1 позволяет определить необходимую кратность превышения минимально различимым контрастом среднеквадратичного значения шума флуктуации числа падающих фотонов при заданной вероятности ложного его измерения. Например, для получения изображения с заданным минимальным контрастом и вероятностью ложного его измерения не более 1% необходимо, чтобы значение заданного минимального контраста не менее чем в 3 раза превышало среднеквадратическое значение флуктуации числа падающих фотонов.
Следовательно, для уменьшения до допустимого значения вероятности ложного измерения информационного параметра элементов разложения ИВС необходимо еще больше увеличивать среднее число падающих на них фотонов, тем самым увеличивая отношение сигнал/шум.
В случае распределения Пуассона при среднем значении числа падающих фотонов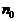 
среднеквадратичное значение шума равно 
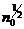, а отношение сигнал/шум -
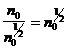. (1.21)
Поэтому для увеличения отношения сигнал/шум ( 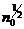) в k раз среднее число падающих фотонов необходимо увеличить в 
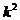раз, таким образом, минимальное число фотонов ( 
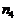), которое необходимо для получения изображения, состоящего из N элементов разложения, с контрастом с можно найти из выражения:
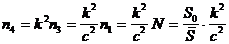, (1.22)
а соответственно число фотонов, приходящихся на один элемент разложения (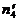 
) будет определяться равенством:
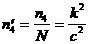. (1.23)
Для экспериментального подтверждения полученного теоретического соотношения (1.22) были выполнены экспериментальные исследования, которые заключались в фоторегистрации изображения специального тест-объекта, предложенного в работе [3], при различных условиях съемки.
Тест-объект представляет собой белое поле, на котором размещались черные круги, причем вдоль строк круги имели по сравнению с фоном одинаковый контраст, но различные диаметры (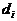 
): диаметр каждого последующего в два раза меньше предыдущего, а по столбцам были размещены круги одного диаметра, но контраст ( 
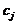) каждого последующего был в два раза меньше предыдущего. В этом случае произведение 
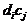остается постоянным вдоль линий, параллельных диагонали тест-объекта.
На рис.1.8 представлены зарегистрированные изображения тест-объекта, полученные при постоянной освещенности, но различных временах экспозиции, причем каждое последующее изображение получено при экспозиции в 4 раза большей, чем предыдущее.
Рис. 1.8
Из соотношения (1.22) следует, что при постоянных условиях съемки
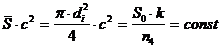. (1.24)
А так как число падающих на тест-объект фотонов ( 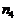) соответствует величине экспозиции (B), то можно считать, что произведение 
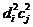обратно пропорционально величине экспозиции:
.
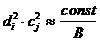Следовательно, для того, чтобы граница различимых дисков на зарегистрированном изображении тест-объекта сдвинулась на один диск вправо (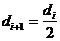 
; 
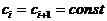) или чтобы граница различимых дисков сдвинулась на один диск вниз ( 
; 
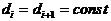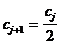) необходимо увеличить экспозицию в 4 раза.
Анализируя полученные фотоизображения тест-объекта, можно сделать вывод, что разрешение элементов изображения при заданной экспозиции зависит как от их размера ( 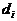), так и от контраста ( 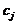), и хорошо согласуется с полученным теоретическим соотношением (1.22).
Действительно, при увеличении экспозиции в 4 раза граница различимых дисков смещается на один шаг вправо, в сторону дисков с диаметром в 2 раза меньше, и на один шаг вниз, в сторону дисков с контрастом в 2 раза меньшим, как и следует из соотношения (1.22).
Для практического использования полученных соотношений (1.22, 1.23) целесообразно привести их к общепринятому виду, то есть к виду с использованием энергетических и светотехнических характеристик. Известно, что падение за время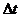 
на некоторую площадку площадью 
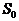числа фотонов n с частотой n соответствует притоку энергии Q [5]:
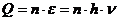, (1.25)
где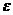 
- энергия одного фотона;
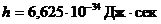- постоянная Планка.
В случае немонохроматического излучения в диапазоне частот от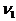 
до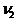 
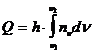, (1.26)
где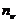 
- распределение числа фотонов по частоте n.
В этом случае энергетический и светотехнический поток излучения (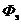 
и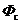 
соответственно) определяют по формулам
; 
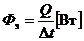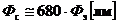, (1.27)
а освещенность энергетическая и светотехническая (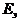 
и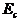 
) по формулам
; 
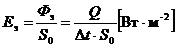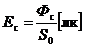. (1.28)
Освещенность ИВС легко может быть измерена и тем самым на основании (1.25, 1.27 и 1.28) определено соответствующее число фотонов, падающих на ИВС. Действительно, для монохроматического излучения
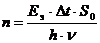(1.29)
и тогда соотношения (1.22 и 1.23) могут быть представлены в следующем виде:
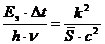. (1.30)
Полученные соотношения (1.30) позволяют получить жесткую функциональную зависимость между легко измеряемыми или конструктивно задаваемыми (как в устройствах считывания) размером элемента разложения (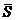 
), параметрами получения символа визуального сообщения ( 
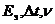) и предельно возможным при заданной допустимой погрешности (k) минимальным контрастом (c), практическое измерение которого трудно выполнимо.
Выразив из (1.30) c - предельно возможный минимальный контраст и подставив его в (1.10), с учетом того, что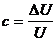 
и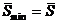 
, получим выражение для максимального предельного количества информации (H), которое может содержаться в символе ИВС единичной площади
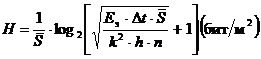(1.31)
или с учетом того, что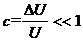 
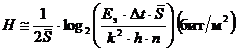. (1.32)
А максимальное предельное среднее количество информации, приходящееся на один элемент разложения, определяется соотношением
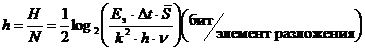. (1.33)
Именно выражения 1.33 и 1.34 могут служить численной мерой качества изображения, потому что предельная энтропия (H) и предельное среднее количество информации, приходящейся на один элемент разложения (h) изображения характеризуют изображения с основополагающей информационной точки зрения, которая во многом определяет их потребительские свойства. Достоинством предложенного метода определения качества изображения является и то, что практическое использование соотношений 1.33 и 1.34 не вызывает трудностей, так как все входящие в них величины могут быть либо легко измерены, либо заданы конструктивно. В качестве примера определим предлагаемым способом качество изображения, которое может быть получено в процессе считывания фотоизображения размером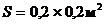 
при освещении его равномерным световым потоком 
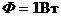, генерируемым гелий-неоновым лазером с длиной волны 
( 
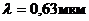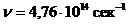). Считывание производится квадратной аппертурой с линейным размером d (мкм) ( 
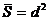) с быстродействием 105 элементов/сек ( 
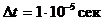) и вероятность ложного измерения различимых уровней контраста не превышающей 0,01% (k=4). В этом случае исходя из выше приведенных соотношений легко найти:
- число различимых уровней контраста (m):
;
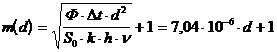- среднее количество информации, приходящейся на один элемент разложения h(d):
;
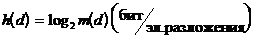- предельное количество информации, содержащейся на всем изображении I(d):
;
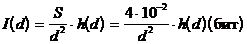- предельная энтропия изображения H(d) при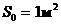 
:
.
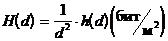В табл.1.2 приведены значения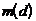 
, 
, 
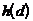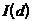и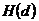 
при различных значениях d.
Табл.1.2
| d(10-6м) | |||||
| ΔS(10-12м) | |||||
| m | |||||
| h(бит/эл.разл.) | 3,0 | 5,2 | 6,2 | 6,7 | 7,5 |
| I(бит) | 1,2·1011 | 8,3·109 | 2,5·109 | 1,2·109 | 4,8·108 |
| H(бит/м2) | 3,0·1012 | 2,1·1011 | 6,2·1010 | 3,0·1010 | 1,2·1010 |
| H(бит/мм2) | 3,0·106 | 2,1·105 | 6,2·104 | 3,0·104 | 1,2·104 |
Важно так же отметить, что в случае регистрации изображений с помощью реальных регистрирующих устройств в регистрирующее устройство попадает лишь часть (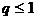 
) фотонов, отраженных символом визуального сообщения, но и эти попадающие в регистрирующее устройство фотоны регистрируются не все, так как квантовый выход регистрирующих устройств ( 
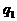), как правило, меньше 1.
Поэтому в этом случае для регистрации изображения символа визуального сообщения с заданным качеством необходимо корректировать полученные соотношения, еще больше увеличивая общее число фотонов, падающих на символ визуального сообщения (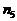 
):
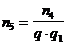. (1.34)
Все выкладки, приведенные выше, касались прежде всего излучения в видимой области спектра (0,4 - 0,7 мкм), однако, так как исходными предпосылками при выводе соотношений является исключительно квантовая теория, то очевидно, что все вышесказанное справедливо и к системам, работающим во всем диапазоне электромагнитного излучения.
Следует также учитывать, что полученные соотношения справедливы только при условии, что линейные размеры элемента разложения значительно превышают длину волны светового излучения, падающего на ИВС, так как они не учитывают волновые эффекты света.
Такой способ определения качества изображения, с нашей точки зрения, является более корректным по сравнению с использованием для этих целей полос заданного контраста, потому что именно с помощью элементов разложения (а не полос) можно построить любое изображение, и современные автоматические методы обработки изображений предполагают разбиение изображения на совокупность элементов, форма которых близка к кругу или квадрату.
Предложенный подход к определению качества изображения хорошо согласуется с методологией современных физических представлений, которые запрещают обсуждать явления сами по себе, независимо от способа их наблюдения. При этом различные явления относятся к объективной реальности (не зависящей от сознания субъекта), а их наблюдение позволяет получить физическую реальность, то есть ту часть объективной реальности, которая может быть познана опытным путем и сознанием субъекта, причем величина этой части зависит от способа наблюдения.
Поэтому очевидно, что качество изображения (его информативность) как физическая реальность, отражающая некую часть объективной реальности, будет определяться условиями наблюдения - степенью освещенности изучаемого объекта.
Моделирование. Информационные модели.
Системы. Общие понятия
Понятие системы является одним из важнейших во многих отраслях науки и техники. Единого общепринятого определения системы не существует, но в самом широком смысле под системой понимают множество, элементы которого закономерно связаны между собой. Элементами множества могут при этом являться те или иные предметы, явления, процессы, знания и многое другое. Соответственно можно говорить о системе уравнений, об оптической системе, о системе передачи данных и т.п.
Таким образом, если событие X в элементе 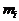множества M определенным образом приводит вероятностным образом к событиям в других элементах 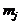, , 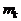и т.д., то можно утверждать, что между элементам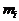и 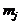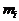и , и 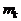и т.д. существует определенная связь. Вот такие множества, в которых наблюдаются определенные взаимосвязи и носят название систем. Понятие системы противопоставляется понятию хаоса. Хаотически можно назвать такое множество элементов 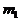, , 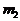, 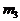..., 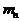, в котором при некотором событии X в элементе 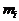могут произойти всевозможные события в остальных элементах.
Существует разновидность систем, у которых событие X в каком-либо элементе однозначно определяет события в других элементах. В таких системах связи между элементами и событиями в них строго и однозначно определены, детерминированы и подобные системы называют детерминированными. Примером таких систем может служить ЭВМ, телевизор и т.п.
В системах иного вида связи между элементами и событиями в них носят вероятностный характер и подобные системы называют вероятностными или стохастическими.
Следует отметить, что строго говоря детерминированных систем вообще не существует, так как даже самая простая система не дает абсолютной гарантии взаимосвязи событий. Поэтому разделение систем на детерминированные и стохастические условно, и строго говоря, все системы стохастические, а детерминированными мы называем те стохастические системы, у которых вероятность ожидаемого события практически равна единице.
Важнейшим свойством системы, являющимся убедительным проявлением закона диалектики о переходе количества в качество, является неаддитивность свойств совокупности элементов, образующих систему, свойство ее нелинейности. Действительно, свойства автомобиля как системы, способной к самостоятельному движению, никак не могут быть получены путем суммирования отдельно взятых свойств ее элементов: колес, топлива, педалей и т.д.
Этот принцип появления в системе свойств, не выводимых из наблюдаемых свойств элементов и связей между ними называют принципом эмерджентности (англ. emergent - неожиданно появляющийся). Этот принцип особенно заметно проявляется в сложных больших системах.
Обязательными компонентами любой системы всегда являются элементы и связи между этими элементами, что в совокупности определяет структуру системы. Структура - это определенная взаимосвязь, взаиморасположение составных частей, характеризующее строение системы.
В общем, любой элемент системы может быть расчленен на более мелкие составляющие (вплоть до молекул). Однако, на практике условились называть элементом системы такую ее часть, которая выполняет определенную специфическую функцию. Следовательно, процесс деления системы на элементы и само понятие элемента условно и весьма относительно.
Элементы любых реальных систем являются некими физическими объектами, которые можно характеризовать их составом, габаритами и т.д. Однако с точки зрения их поведения в системе в большинстве случаев можно отвлечься от их физических свойств и характеризовать их только возможностью образовывать те или иные виды связей: вещественных, энергетических и информационных - с другими элементами и с внешней по отношению к системе средой.
Необходимо отметить, что все три вида связей существуют всегда неотделимо друг от друга, но в зависимости от того, какой вид связи является определяющим, данную связь можно отнести к одному из перечисленных видов.
Следовательно, важнейшей характеристикой элемента в системе является его способность к установлению связей, т.е. к порождению (генерации) или восприятию (поглощению) связей.
Таким образом, при исследовании, анализе и моделировании систем пользуются идеализированными моделями элементов и систем.
Идеализированный элемент представляет некий абстрактный элемент, у которого отсутствуют любые физические свойства кроме способности к реализации связей с другими элементами.
Совокупность идеализированных элементов, объединенных необходимыми связями, образует идеализированную модель системы.
Как указывалось выше, любой элемент можно рассматривать как совокупность более мелких элементов, то есть как систему.
Таким образом, любая система имеет, как правило, иерархическую структуру, то есть многоуровневую структуру. При решении практических задач достаточным оказывается выделение ограниченного числа ступеней иерархии. При этом системы низшего уровня называют подсистемами систем высокого уровня, которые в свою очередь являются подсистемами систем еще более высокого уровня и т.д., вплоть до так называемой суперсистемы, находящейся на верхней ступени иерархической структуры.
Простой называют такую систему, работу которой можно исследовать как нечто целое без разбиения ее на подсистемы.
Большими и сложными называют системы с разветвленной структурой и значительным количеством взаимосвязанных и взаимодействующих элементов.
По характеру перехода из одного состояния в другое системы делят на статические и динамические. Динамическими называют такие системы, переход которых в новое состояние не может совершиться мгновенно, а происходит в результате некоторого процесса, растянутого во времени. Строго говоря, все реальные системы являются динамическими, однако, если временем перехода можно пренебречь, то говорят о статических системах.
Работа любой системы происходит в некоторой окружающей ее внешней среде, не входящей в систему, но определенным образом взаимодействующую с ней. В принципе внешняя среда всегда оказывает влияние на любые системы. Однако в зависимости от степени и практической значимости этого влияния системы подразделяются на открытые и закрытые.
Процессы в открытых системах определяются влиянием внешней среды и сами оказывают на нее воздействие. Следовательно, их функционирование определяется как внутренней, так и внешней информацией, поступающей на входы системы.
Закрытые или замкнутые системы - это системы, в процессе функционирования которых используется только та информация, которая вырабатывается внутри самой системы, так что все взаимодействия между элементами системы определяются процессами, протекающими внутри самой системы.
При изучении явлений и процессов в любых системах можно, очевидно, применять два подхода. Один из них - локальный - заключается в изучении структуры и функциональных особенностей автономных отдельно взятых элементов системы. Другой - системный подход - представляет исследование способов организации элементов системы в единое целое и взаимного воздействия системы, ее подсистем и элементов друг на друга.
Состояние любой реальной системы в каждый данный момент времени можно описать с помощью некоторого множества характеризующих систему величин - параметров. Количество параметров даже для относительно простой системы может быть очень большим, поэтому практически для описания систем, используют лишь наиболее существенные, характерные для нее параметры, соответствующие конкретным целям изучения.
Так, при исследовании здоровья человека с точки зрения освобождения его от работы принимают во внимание температуру и кровяное давление, и при проверки подготовки абитуриента интересуются совсем иными параметрами: грамотностью, умением решать задачи.
Для описания состояния и движения системы можно применять различные способы, но в технике особенно широкое применение находит математическое описание, которое для наглядности часто интерпретируют графиками, отображающими протекание тех или иных процессов. Наиболее удобным из них является метод описания состояния систем и их движения в пространстве состояний или фазовом пространстве.
Пространством состояний системы называется пространство, каждой точке которого однозначно соответствует определенное состояние рассматриваемой динамической системы, а каждому процессу изменения состояний системы соответствует определенная траектория перемещения изображающей точки в пространстве.
В этом методе используется фазовое пространство (n-мерное Евклидово пространство), по осям которого откладываются значения всех n обобщенных координат рассматриваемой динамической системы. При этом взаимно однозначное соответствие между состояниями системы и точками фазового пространства достигается выбором числа измерений n-мерного пространства, равного числу обобщенных координат рассматриваемой системы.
Параметры некоторой системы можно обозначить символами 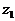, , 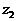,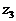..., , 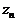которые можно рассматривать как компоненты вектора Z n-мерного пространства
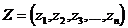. (5.1)
Параметры 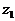, , 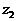,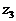..., 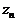называют фазовыми координатами системы, а состояние (фазу) системы изобразим точкой Z в фазовом пространстве.
В реальных условиях работы системы ее параметры (фазовые координаты), как правило, могут меняться лишь в некоторых ограниченных пределах. Область фазового пространства, за пределы которой не может выходить изображающая точка, называют областью допустимых состояний системы. При исследовании и проектировании систем всегда исходят из того, что система остается в пределах ее допустимых значений. Если изображающая точка выйдет за пределы этой области, то это грозит разрушением системы.
Фактически в нормальных условиях эксплуатации параметры системы изменяются в значительно более узких пределах. И совокупность изображающих их точек образует область рабочих состояний. Геометрически область рабочих состояний всегда должна находиться внутри области допустимых значений.
Переход системы из одного состояния в другое будет характеризова