Применение операционного исчисления к решению линейных дифференциальных уравнений и их систем
Операционный метод позволяет просто решать линейные дифференциальные уравнения с постоянными коэффициентами, в правых частях которых стоят оригиналы. Оператор Лапласа применяется к обеим частям такого уравнения, после чего получается линейное алгебраическое уравнение относительно изображения неизвестной функции.
Пусть требуется найти частное решение линейного дифференциального уравнения, например, второго порядка с постоянными коэффициентами:
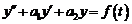 ,
,
удовлетворяющее начальным условиям
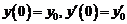 .
.
(Для уравнений более высоких порядков решение аналогично.)
Будем считать, что искомая функция 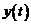 вместе с ее производными и функция
вместе с ее производными и функция  являются оригиналами. Пусть
являются оригиналами. Пусть 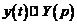 . Используя теорему о дифференцировании оригинала, находим изображения производных, входящих в уравнение:
. Используя теорему о дифференцировании оригинала, находим изображения производных, входящих в уравнение:
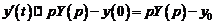 и
и
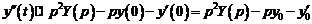 .
.
Далее, пусть для правой части уравнения 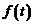 изображением будет
изображением будет 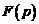 . Тогда, применяя преобразование Лапласа к обеим частям уравнения и пользуясь свойством линейности изображения, получим операторное (или изображающее) уравнение:
. Тогда, применяя преобразование Лапласа к обеим частям уравнения и пользуясь свойством линейности изображения, получим операторное (или изображающее) уравнение:
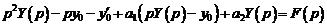 .
.
Это уравнение является линейным уравнением относительно неизвестной функции 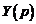 . Из него находим
. Из него находим
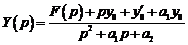 .
.
Наконец по изображению 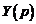 восстанавливаем оригинал
восстанавливаем оригинал 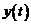 , который в силу теоремы единственности оригинала и является частным решением заданного уравнения.
, который в силу теоремы единственности оригинала и является частным решением заданного уравнения.
Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами.
Примеры.
1. Используя операционное исчисление, найти частное решение дифференциального уравнения 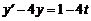 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 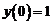 .
.
Решение. Пусть 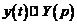 , тогда
, тогда 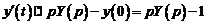 , кроме того
, кроме того 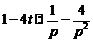 . Таким образом, применяя преобразование Лапласа к обеим частям уравнения, приходим к операторному уравнению
. Таким образом, применяя преобразование Лапласа к обеим частям уравнения, приходим к операторному уравнению
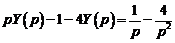 .
.
Выразим из полученного уравнения функцию 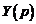 :
:
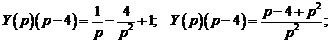
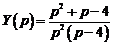 .
.
Представим эту рациональную дробь как сумму простейших дробей:
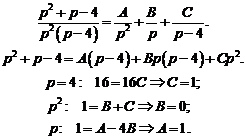
Итак, 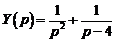 . Следовательно, решением заданного дифференциального уравнения будет функция, которая является оригиналом для полученного изображения:
. Следовательно, решением заданного дифференциального уравнения будет функция, которая является оригиналом для полученного изображения:
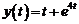 .
.
2. Найти частное решение дифференциального уравнения 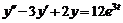 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 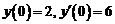 .
.
Решение. Пусть 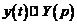 . Тогда
. Тогда
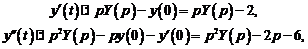
и 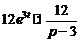 .
.
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
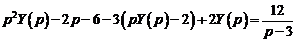 ,
,
или
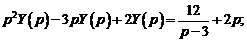
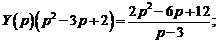
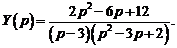
Методом неопределенных коэффициентов найдем разложение этой дроби в сумму простейших дробей.
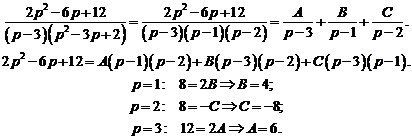 Таким образом,
Таким образом, 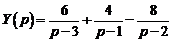 . Следовательно, частное решение данного дифференциального уравнения будет
. Следовательно, частное решение данного дифференциального уравнения будет
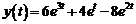 .
.
 3. Решить задачу Коши
3. Решить задачу Коши 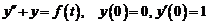 , где функция
, где функция  задана графически на рисунке.
задана графически на рисунке.
Решение. Пусть 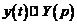 . Тогда
. Тогда 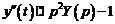 . Найдем изображение функции
. Найдем изображение функции  , воспользовавшись теоремой запаздывания. Зададим
, воспользовавшись теоремой запаздывания. Зададим  аналитически, используя единичную функцию Хевисайда:
аналитически, используя единичную функцию Хевисайда:
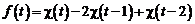 .
.
Тогда
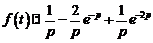 .
.
Операторное уравнение принимает вид
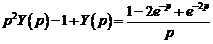 .
.
Находим из него неизвестное изображение 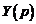 :
:
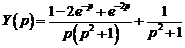 .
.
Разложим дробь 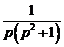 в сумму простейших дробей.
в сумму простейших дробей.
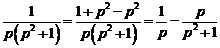 .
.
(При разложении можно использовать метод неопределенных коэффициентов.) Следовательно,
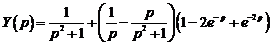 .
.
Еще раз используя теорему запаздывания, найдем искомое решение дифференциального уравнения:
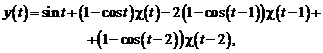
или
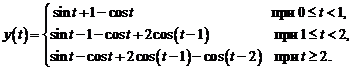
4.Операционным методом решить систему линейных дифференциальных уравнений
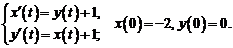
Решение. Пусть 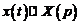 ,
, 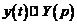 . Тогда
. Тогда 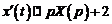 ,
, 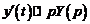 и
и 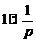 . Система операторных уравнений принимает вид
. Система операторных уравнений принимает вид
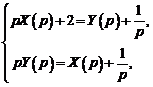 или
или 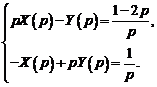
Получили систему линейных алгебраических уравнений относительно изображений 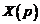 и
и 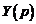 . Для ее решения используем метод Крамера.
. Для ее решения используем метод Крамера.
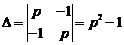 ,
,
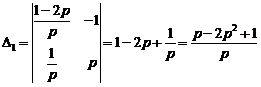 ,
,
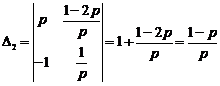 .
.
Итак,
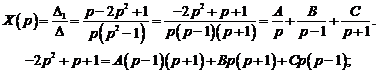
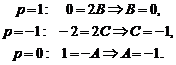
Тогда 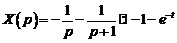 .
.
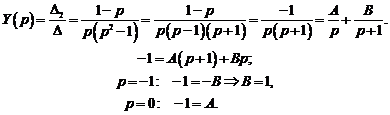
Следовательно, 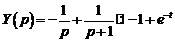 .
.
Таким образом, решением системы дифференциальных уравнений, удовлетворяющим заданным начальным условиям являются функции 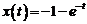 ,
, 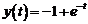 .
.
5.Операционным методом решить систему линейных дифференциальных уравнений
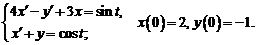
Решение. Перейдем к изображениям искомых функций:
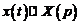 ,
, 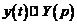 ,
,
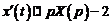 ,
, 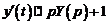 .
.
Кроме того,
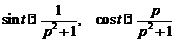 .
.
Тогда система операторных уравнений будет иметь вид
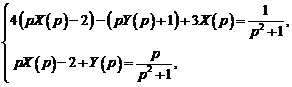
или
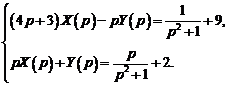
Решим полученную систему методом Крамера.
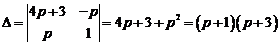 ,
,
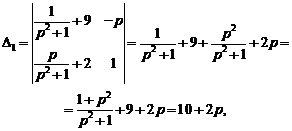
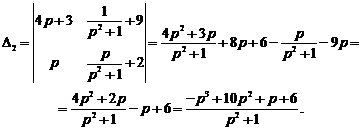
Выпишем изображения искомых функций:
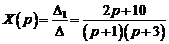 ,
,
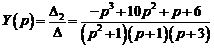 .
.
Используя метод неопределенных коэффициентов, восстановим оригиналы.
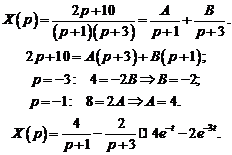
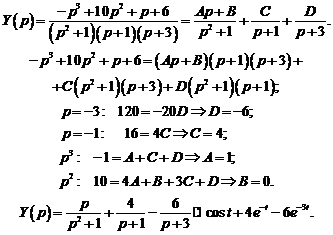
Таким образом, решением системы уравнений являются функции 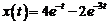 ,
, 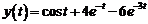 .
.
Задачи для практических занятий и самостоятельной работы по теме Операционное исчисление»
1.Найдите изображения следующих функций:
1) 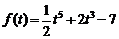 .Ответ:
.Ответ: 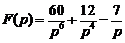 .
.
2) 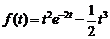 .Ответ:
.Ответ: 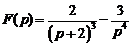 .
.
3) 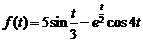 .
.
Ответ: 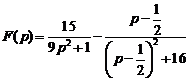 .
.
4) 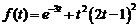 .Ответ:
.Ответ: 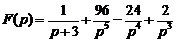 .
.
5) 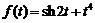 . Ответ:
. Ответ: 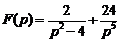 .
.
6) 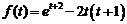 .Ответ:
.Ответ: 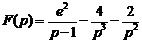 .
.
7) 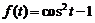 . Ответ:
. Ответ: 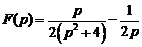 .
.
8) 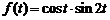 .Ответ:
.Ответ: 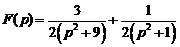 .
.
9) 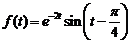 .
.
Ответ: 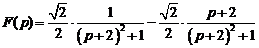 .
.
10) 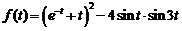 .
.
Ответ: 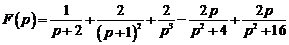 .
.
11) 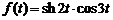 .
.
Ответ: 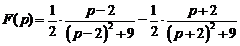 .
.
12) 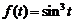 .Ответ:
.Ответ: 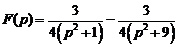 .
.
13) 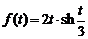 .Ответ:
.Ответ: 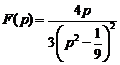 .
.
14) 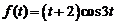 . Ответ:
. Ответ: 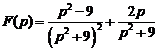 .
.
15) 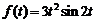 .Ответ:
.Ответ: 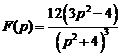 .
.
16) 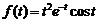 .Ответ:
.Ответ: 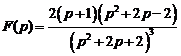 .
.
2.Найдите оригиналы по заданным изображениям:
1) 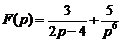 . Ответ:
. Ответ: 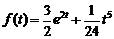 .
.
2) 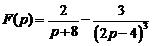 . Ответ:
. Ответ: 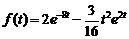 .
.
3) 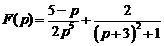 .
.
Ответ: 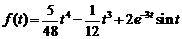 .
.
4) 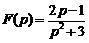 . Ответ:
. Ответ: 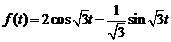 .
.
5) 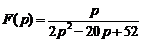 . Ответ:
. Ответ: 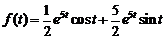 .
.
6) 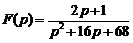 .
.
Ответ: 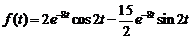 .
.
7) 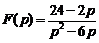 . Ответ:
. Ответ: 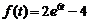 .
.
8) 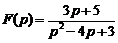 . Ответ:
. Ответ: 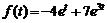 .
.
9) 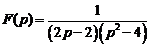 . Ответ:
. Ответ: 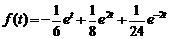 .
.
10) 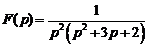 . Ответ:
. Ответ: 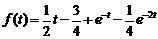 .
.
11) 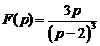 . Ответ:
. Ответ: 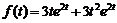 .
.
12) 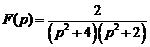 .
.
Ответ: 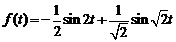 .
.
13) 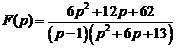 .
.
Ответ: 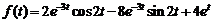 .
.
14) 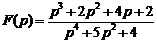 . Ответ:
. Ответ: 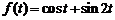 .
.
15) 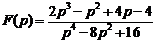 .
.
Ответ: 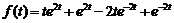 .
.
16) 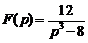 . Ответ:
. Ответ: 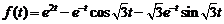 .
.
3.Найдите свертку функций и ее изображение:
1) 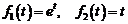 .
.
Ответ: 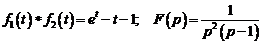 .
.
2) 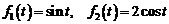 .
.
Ответ: 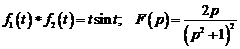 .
.
3) 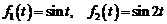 .
.
Ответ: 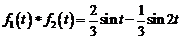 ;
;
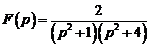 .
.
4) 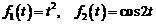 .
.
Ответ: 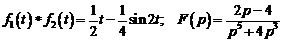 .
.
5) 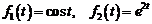 .
.
Ответ: 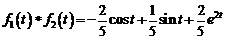 ;
;
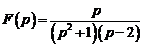 .
.
4.Найдите оригиналы для следующих изображений, используя теорему свертывания:
1) 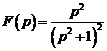 . Ответ:
. Ответ:  .
.
2) 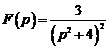 . Ответ:
. Ответ: 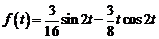 .
.
3) 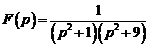 . Ответ:
. Ответ: 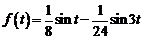 .
.
4) 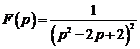 . Ответ:
. Ответ: 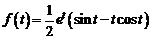 .
.
5.Используя теорему запаздывания, найдите изображения следующих функций:
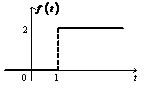 1)
1)
 Ответ:
Ответ: 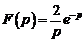 .
.
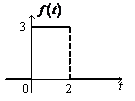 2)
2)
 Ответ:
Ответ: 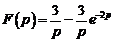 .
.
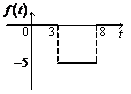
3)
Ответ: 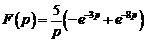 .
.
4) 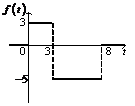
 Ответ:
Ответ: 
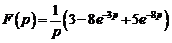 .
.
5) 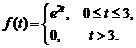 Ответ:
Ответ: 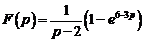 .
.
6) 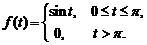
Ответ: 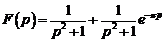 .
.
6.Используя теорему запаздывания, найдите оригиналы для следующих изображений:
1) 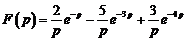 . Ответ:
. Ответ: 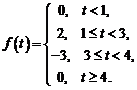
2) 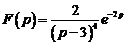 . Ответ:
. Ответ: 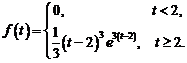
3) 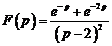 .
.
Ответ: 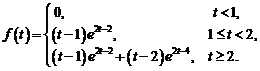
4) 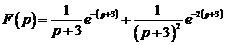 .
.
Ответ: 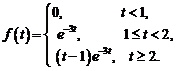
7.Решите дифференциальные уравнения операционным методом:
1) 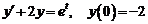 . Ответ:
. Ответ: 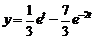 .
.
2) 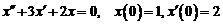 . Ответ:
. Ответ: 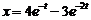 .
.
3) 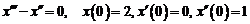 . Ответ:
. Ответ: 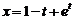 .
.
4) 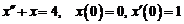 . Ответ:
. Ответ: 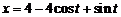 .
.
5) 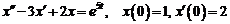 .
.
Ответ: 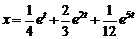 .
.
6) 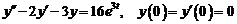 .
.
Ответ: 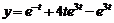 .
.
7) 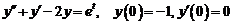 .
.
Ответ: 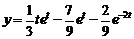 .
.
8) 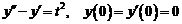 .
.
Ответ: 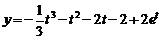 .
.
9) 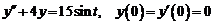 .
.
Ответ: 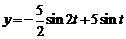 .
.
10) 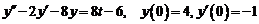 .
.
Ответ: 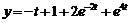 .
.
11) 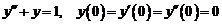 .
.
Ответ: 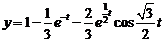 .
.
12) 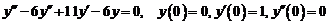 .
.
Ответ: 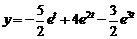 .
.
13) 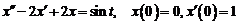 .
.
Ответ: 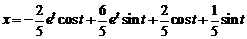 .
.
14) 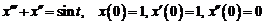 .
.
Ответ: 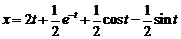 .
.
15) 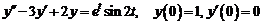 .
.
Ответ: 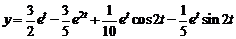 .
.
16) 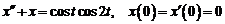 .
.
Ответ: 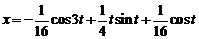 .
.
17) 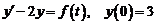 , где
, где 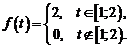
Ответ: 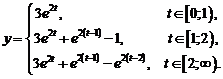
18) 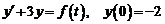 , где
, где 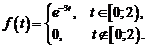
Ответ: 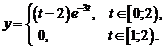
8.Решите системы дифференциальных уравнений операционным методом:
1) 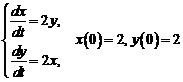 . Ответ:
. Ответ: 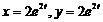 .
.
2) 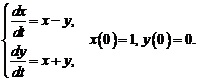 Ответ:
Ответ: 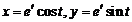 .
.
3) 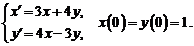
Ответ: 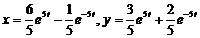 .
.
4) 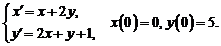
Ответ: 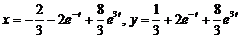 .
.
5) 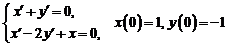 .
.
Ответ: 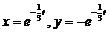 .
.
6) 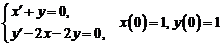 .
.
Ответ: 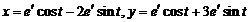 .
.
7) 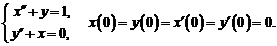
Ответ:  .
.
8) 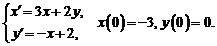
Ответ: 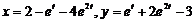 .
.
9) 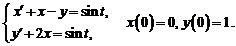
Ответ: 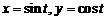 .
.
10) 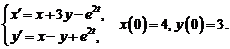
Ответ: 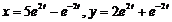 .
.
11) 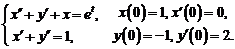
Ответ: 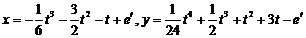 .
.
