В задачах транспорта и связи
Компьютерные методы
Обработки информации
и
Распознавание образов
В задачах транспорта и связи
Часть 1: Пакет MATLAB
Буслаев А.П., Кузьмин Д.М., Яшина М.В.
МТУСИ
Содержание
1. Начальные сведения о математическом пакете MATLAB
2. Основные конструкции MATLAB.
3. Основные команды для цифровой обработки изображений.
4. Программирование в MATLAB
5. Визуализация результатов вычислений.
6. Статистические функции обработки изображений.
7. Управление параметрами изображений.
8. Фильтрация изображений.
9. Выделение контуров.
10. Пример обработки изображения для решения практических задач анализа качества дорожного покрытия.
11. Литература
Введение
С развитием цифровых фото- и видеокамер заметно расширилась база изображений, и стали актуальными задачи их автоматической обработки. Приложения интеллектуальных систем, основанные на анализе изображений, т.н. «техническое зрение», - самые разнообразные, от создания роботов в производстве до гуманитарных помощников в жизне-деятельности.
В последнее время обеспечение безопасности человека приобретает первостепенное значение в связи с наметившимися тенденциями к изменению климата, возрастанием энерго-насыщенности человеческой жизни, обострением конкуренции сообществ за ресурсы, усложнением межличностных отношений.
Таким образом, обеспечение равных справедливых условий конкуренции за жизненное пространство – одно из важнейших направлений совершенствования интеллектуальных устройств, основанных на анализе звука, изображений и других «отпечатков» человеческой жизни.
В первой части планируемой серии рассматриваются возможности стандартного пакета MATLAB. Пакет естественно-научных вычислений – MATLAB – это интерактивная система, в которой основным элементом данных является массив, матрица, как обобщение понятия числа. Возможности пакета MATLAB включают в себя математические операции, создание алгоритмов, анализ данных и визуализацию, разработку приложений с доступом в форме графического интерфейса.
Изначально пакет создавался для практического применения методов линейной алгебры и теории матриц в различных областях машиностроения и науки. Однако, в процессе развития приобрел качества самостоятельного продукта, ориентированного в частности, и на обработку сигналов, звука и изображений.
Приведенные упражнения должны способствовать более полному усвоению материала.
Редактор командной строки
Различные стрелки и управляющие клавиши на клавиатуре позволяют вызывать, редактировать и многократно использовать команды, набранные ранее. Например, предположим, что допущена ошибка при вводе выражения 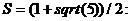
>> 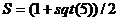 % т.е. в сочетании sqrt пропущена буква r
% т.е. в сочетании sqrt пропущена буква r
MATLAB ответит вам предупреждением
Undefined function or variable `sqt`.
Вместо того чтобы заново набирать всю строку, можно нажать клавишу . На экране изобразится ошибочно введенная команда. Далее используется клавиша для перемещения курсора и вставки пропущенной буквы “r”. Повторное использование клавиши вызовет предыдущую строку. Ниже приведен список клавиш, позволяющих редактировать команды в командном окне I, рис. 1.
Список доступных клавиш редактирования в командной строке зависит также от настроек компьютера.
| | Ctrl-p | Вызов предыдущей строки |
| ¯ | Ctrl-n | Вызов последующей строки |
| Ctrl-b | Движение назад на один символ | |
| ® | Ctrl-f | Движение вперед на один символ |
| Ctrl-® | Ctrl-r | Движение вправо на одно слово |
| Ctrl- | Ctrl-l | Движение влево на одно слово |
| Home | Ctrl-a | Переход на начало строки |
| End | Ctrl-e | Переход на конец строки |
| Esc | Ctrl-u | Очистка строки |
| Del | Ctrl-d | Удаление символа за курсором |
| Backspace | Ctrl-h | Удаление символа перед курсором |
| Ctrl-k | Удаление до конца строки |
Упражнение 1.1.Присвоить переменной X арифметическое выражение 2/5 + 1,1 * 2 и проверить результат.
Упражнение 1.2. Записать значение 1/0 переменной Y.
Упражнение 1.3.Присвоить Z алгебраическое выражение A * (A +2) и проверить результат.
Упражнение 1.4.Вычислить arcsin(2).
Упражнение1.5. Вычислить 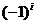 .
.
Сообщения MATLAB о некорректных действиях пользователя:
Warning: Divide by zero.
??? Undefined function or variable 'A'.
Error: The expression to the left of the equals sign is not a valid target for an assignment.
Основные конструкции MATLAB
Пример 2.1.
1. 201 – целое число, тип unit8 или int8
2. -122 – целое число, тип int8
3. -8.256 – действительное число, тип single
4. 47584930274847.9994 - действительное число, тип double:
>> x=47584930274847.9994
x = % представления числа типа
4.7585e+013 % double в MATLAB
5. АВС1 – char, символьный тип
Упражнение 2.1.
а). Почему число -122 не относится к типу unit8?
б). Если a=2 и b=16, к какому типу следует отнести результат операции деления c=a/b, чтобы он был по возможности более точным?
в). Если a, b и c принадлежат unit8, a=45, b=17, c=a/b, чему равно c?
Массивы.
Массивы (array) представляют собой структуры, используемые в языках программирования для работы с наборами (упорядоченными последовательностями) чисел одного типа. Естественно, что компьютер может работать только с конечными наборами чисел. Таким образом, массив – это функция на упорядоченной последовательности чисел  , таких что
, таких что  ,
,  , количество чисел в
, количество чисел в  . Число kназывается размерностью массива или числом индексов массива.
. Число kназывается размерностью массива или числом индексов массива.
Например, Х={f(1),f(2),f(3),f(4),f(5)}={5,10,34,56,70} – одномерный массив целых чисел, где А1={1,2,3,4,5};
 |  |  |  |
f(1,1), f(1,2), f(1,3), f(1,4) 3.5, - 6, 90,1.9
Y= f(2,1), f(2,2), f(2,3), f(2,4) = 5.1 1.1, 40, 48 -
f(3,1), f(3,2), f(3,3), f(3,4) -60, 3.4,-1.6, 9
двумерный массив действительных чисел, где А1={1,2,3}, А2={1,2,3,4}.
Двумерный массив, таким образом, является структурой программирования, соответсвующей математическому понятию матрица. Визуально матрица представляется в виде таблицы чисел

А = ,где m – число строк, n – число столбцов, прозвольный элемент  имеет два индекса: i - номер строки, j – номер столбца. Размером матрицы А называется пара m ´ n.
имеет два индекса: i - номер строки, j – номер столбца. Размером матрицы А называется пара m ´ n.
Каждый язык программирования имеет ограничения на k-число наборов в массиве. В С++ величина k не превосходит 12. Для MATLAB наиболее часто используются случаи k=1 и 2.
Одномерные массивы (конечная последовательность чисел) инициализируются в MATLAB в квадратных скобках, разделители – пробелы или запятые. Индексация массивов начинается с единицы.
Пример 2.2.
а) >> v=[3V5V6V7V2] % Ввод целочисленного вектора
v = % Значение переменной v
3 5 6 7 2
б)>> v(2) % Запрос значения координат
% вектора v с номером 2
ans =
в)>> v2=v(2);v2 % Запрос значения координат
% вектора v с номером 2
v2 =
г)>> v(1:3) % Запрос значений координат
% вектора v начиная с номера
% 1 до номера 3
ans =
3 5 6
Замечание. В примере 2.2.б в запросе не указано точное имя переменной вывода, поэтому в ответе используется имя “ans”.
В примере 2.2.в мы указали имя выводимой переменной “v2” и в ответе компьютера оно появилось.
Для доступа к блоку элементов массива используется символ «:».
Для ввода матриц (прямоугольной таблицы) в качестве разделителя строк используется символ «;».
Пример 2.3.
а) Ввод матрицы А размер 3 х 3.
>> A = [1V2V3;V2V3V4;V5V4V3] % Ввод элементов
% матрицы А 3х3
A = % Проверка
1 2 3
2 3 4
5 4 3
б) Ввод ранжированного вектора x= {1, 3, 5, 7, 9}
>> x = 1:2:9 % Указываются начальное значение,
% разделитель ‘:’, шаг, разделитель,
% конечное значение
Операторы
Операторы MATLAB разделены на три основные категории:
- арифметические операторы;
- операторы сравнения;
- логические операторы.
Операции с числами
В MATLAB существуют следующие арифметические операторы:
| + | сложение |
| - | вычитание |
| * | умножение |
| ^ | возведение в степень |
Операции с матрицами
| + | сложение |
| - | вычитание |
| * | умножение |
| / | правостороннее деление |
| \ | левостороннее деление |
| ^ | возведение в степень |
| ' | транспонирование |
Следующие операторы могут быть применены к матрицам (двумерным массивам):
а) A+B - сложение матриц одинакового размера,
б) A-B - вычитание матриц одинакового размера,
в) A*B - обозначает произведение матриц A и B по правилам линейной алгебры (число столбцов А равно числу строк В):
если  , то
, то 
г) A .* B - обозначает операцию над матрицами одинакового размера, результатом которой является матрица такого же размера, что A и B, каждый элемент которой получается как произведение соответствующих элементов исходных матриц; если  , то
, то 
д) В/А - возвращает матрицу, равную  . Результат
. Результат  является решением матричного уравнения
является решением матричного уравнения  . Использование оператора в виде В. /А создает матрицу С с элементами
. Использование оператора в виде В. /А создает матрицу С с элементами 
е) A\B - возвращает матрицу, равную  . Результат
. Результат  является решением матричного уравнения
является решением матричного уравнения  . Использование оператора в виде В.\А создает матрицу С с элементами
. Использование оператора в виде В.\А создает матрицу С с элементами 
ж) A’ - транспонирование матрицы (aij ® (j,i)).
Замечание.Левостороннее и правостороннее операции деления матриц связаны соотношением 
Пример 2.4. Применим операции деления к числам 4 и 2 как
матрицам размера 1*1. Результатом действия оператора 4/2 будет число 2, а 4\2 дает соответственно 0.5.
Логические операторы
Логических операторов всего три: «И» - “&”, «ИЛИ» - “|”, «НЕ» - “~”. Результатом логического оператора также является матрица, состоящая из «0» и «1», причем в исходных операндах 0 обозначает «ложь», а любое не нулевое число – «истина».
Пример 2.6.Пример использования оператора “|”:
>>u = [0 0 1 1 0 1];
>>v = [0 1 1 0 0 1];
>>u | v % Поэлементная
% дизъюнкция векторов
% u и v
ans =
0 1 1 1 0 1
Символьные вычисления
Большой интерес для применения методов дифференциального и интегрального исчисления представляют так называемые символьные вычисления. Для их реализации используется пакет расширения Symbolic Math.
Символьные переменные – это специальный тип переменных, которые можно испльзовать как входные параметры символьных команд. К символьным командам относятся математические преобразования над функциональными представлениями y = f(x), такиекак упрощение алгебраических выражений, раскрытие скобок в многочленах, операции интегрирования и дифференцирования функций, и т.д.
Основные команды пакета Symbolic Math:
1. x = sym ('x') - создаёт символьную переменную с именем х.
2. x = sym(a)- преобразует десятичную дробь a в обыкновенную (p/q).
>> x =sym( 2.5);
x =
5/2 % Результат
3. Лексикографическое упорядочивание буквенных символов (сортировка) – т.е. перестановка их в порядке, определенном соответствующим алфавитом, в примере - латинским.
>> syms a b c d e x
>> sort ([a c e b d])
ans =
[a,b,c,d,e] % Результат
4. int(s) - возвращает первообразную функции s.
5. diff(s) – дифференцирует функцию s.
6. R = jacobian(f,v), где f- функция; v - вектор аргументов f. Возвращает якобиан.
Пример 2.7.
Перед использованием функций пакета символьных вычислений необходимо определить тип переменной x, как символический.
a) Вычислить интеграл 
>> syms x
>> int(x^2-1) % вычисление первообразной
ans =
1/3*x^3-x
b) Найти производную  .
.
Производную можно найти, используя оператор
>> diff(x^2-1,x) % нахождение производной
ans =
2*x
с) Даны функции зависимости координат {x, y, z} от параметров r, l, f.
 x = r× cos(l)×cos(f);
x = r× cos(l)×cos(f);
y = r× cos(l)×sin(f);
z = r× sin(l);
Найти якобиан замены координат.
>> syms r l f % объявление переменных r, l, f как
% символьных
>> x = r*cos(l)*cos(f);
>> y = r*cos(l)*sin(f);
>> z = r*sin(l);
>> J = jacobian([x; y; z], [r l f])% вычисление
% якобиана
J = % результат
[cos(l)*cos(f), -r*sin(l)*cos(f), r*cos(l)*sin(f)]
[cos(l)*sin(f), -r*sin(l)*sin(f), r*cos(l)*cos(f)]
[sin(l), r*cos(l), 0]
Упражнение 2.1. Найти  ,
,  .
.
Упражнение 2.2. Найти  .
.
Упражнение 2.3. Вычислить  ; если
; если  .
.
Упражнение 2.4. Найти  .
.
Бинарные изображения
Черно-белое изображение в MATLAB представляется матрицей в бинарном виде. Элементы матрицы бинарных (двоичных) изображений являются бинарными и могут принимать только 2 значения - 0 и 1, обозначающих соответственно черный и белый цвета (тип logical). Таким образом, двоичное изображение задается матрицей из нулей и единиц.
Пример 3.1.Задано бинарное изображение на рис.4. Найти его матрицу.
На следующем рисунке приведено бинарное изображение размером 12*12 и его матрица (черная рамка в один пиксел).

0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 1 1 0
0 0 0 0 0 0 0 0 1 1 1 0
0 0 0 0 0 0 0 1 1 1 1 0
0 0 0 0 0 0 1 1 1 1 1 0
0 0 0 0 0 1 1 1 1 1 1 0
0 0 0 0 1 1 1 1 1 1 1 0
0 0 0 1 1 1 1 1 1 1 1 0
0 0 1 1 1 1 1 1 1 1 1 0
0 0 0 0 0 0 0 0 0 0 0 0
Рис.4. Бинарный образ изображения
3.2.2. Полутоновые изображения (изображения с градацией серого)(grayscale)
Если монохромное изображение учитывает переходы от черного к белому через оттенки серого, то формат представления числа от граничных значений 0 и 1 расширяется до отрезка [min_color, max_color]. Такое изображение называется полутоновым.
В этом случае матрица состоит из целых чисел типа uint8(см. п. 2), т.е. минимальное значение 0, максимальное – 255 (всего  вариантов). Возможны также типы uint16 и double из интервала [0,1].
вариантов). Возможны также типы uint16 и double из интервала [0,1].
Пример 3.2.На рис.5 показан прямоугольник, содержащий темный треугольник, в полутоновом формате и его матрица. Можно видеть, что пикселы, соответствующие темному треугольнику, имеют меньшие значения интенсивности, чем верхний светлый угол.
 |
255 249 255 255 246 255 255 255 242 255 240 128
255 252 252 252 255 251 255 238 255 234 128 128
250 255 255 253 255 253 242 255 235 128 128 128
255 254 255 255 240 255 243 248 128 128 128 128
255 244 250 249 255 240 255 128 128 128 128 128
255 239 253 255 241 255 121 127 128 128 128 128
242 255 252 246 255 128 128 128 128 128 128 128
255 244 255 238 129 128 128 128 128 128 128 128
242 255 240 128 128 128 128 128 128 128 128 128
255 234 128 128 128 128 128 128 128 128 128 128
235 128 128 128 128 128 128 128 128 128 128 128
128 128 128 128 128 128 128 128 128 128 128 128
Рис.5. Полутоновый образ изображения
3.2.3. Цветные изображения RGB(true color RGB)
Каждому пикселу графического изображения соответствует трехмерный вектор. Таким образом, изображению соответствуют три матрицы, которые в дальнейшем будем называть цветовыми картами, причем матрица, соответствующая первому индексу – матрица интенсивности красной компоненты, второму – зеленой, третья – синей.
Пример 3.3. Цветное изображение и три его матрицы. На рис.6 квадрат закрашен в серый (верхний треугольник), красный (против часовой стрелки), розовый и белый цвета, имя графического образа – «treyg_3».

Рис.6. Принтерный образ цветного изображения
Карта интенсивности красной компоненты RGB рис.6.
>>treyg_3(:,:,1) =
| 0 0 0 0 0 0 0 0 0 0 0 0 0 |
| 0 0 128 128 128 128 128 128 128 128 128 255 0 |
| 0 255 0 128 128 128 128 128 128 128 255 255 0 |
| 0 255 255 0 128 128 128 128 128 128 255 255 0 |
| 0 255 255 0 128 128 128 128 128 255 255 255 0 |
| 0 255 255 255 0 128 128 128 255 255 255 255 0 |
| 0 255 255 255 255 0 128 255 255 255 255 255 0 |
| 0 255 255 255 255 255 0 255 255 255 255 255 0 |
| 0 255 255 255 255 255 255 0 255 255 255 255 0 |
| 0 255 255 255 255 255 255 255 0 255 255 255 0 |
| 0 255 255 255 255 255 255 255 255 0 255 255 0 |
| 0 255 255 255 255 255 255 255 255 255 0 255 0 |
| 0 255 255 255 255 255 255 255 255 255 0 255 0 |
| 0 255 255 255 255 255 255 255 255 255 255 0 0 |
Карта интенсивности зеленой компоненты RGB
>>treyg_3(:,:,2) =
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 128 128 128 128 128 128 128 128 128 0 0
0 0 0 128 128 128 128 128 128 128 0 255 0
0 0 0 0 128 128 128 128 128 128 0 255 0
0 0 0 0 128 128 128 128 128 0 255 255 0
0 0 0 0 0 128 128 128 0 255 255 255 0
0 0 0 0 0 0 128 0 255 255 255 255 0
0 0 0 0 0 0 0 255 255 255 255 255 0
0 0 0 0 0 0 0 0 255 255 255 255 0
0 0 0 0 0 0 0 0 0 255 255 255 0
0 0 0 0 0 0 0 0 0 0 255 255 0
0 0 0 0 0 0 0 0 0 0 0 255 0
0 0 0 0 0 0 0 0 0 0 0 255 0
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
Карта интенсивности синей компоненты RGB
>>treyg_3(:,:,3) =
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 128 128 128 128 128 128 128 128 128 0
0 0 0 128 128 128 128 128 128 128 0 255 0
0 0 0 0 128 128 128 128 128 128 0 255 0
0 0 0 0 128 128 128 128 128 0 255 255 0
0 0 0 0 0 128 128 128 0 255 255 255 0
0 0 0 0 0 0 128 0 255 255 255 255 0
0 0 0 0 0 0 0 255 255 255 255 255 0
0 0 0 0 0 0 255 0 255 255 255 255 0
0 0 0 0 0 255 255 255 0 255 255 255 0
0 0 0 0 255 255 255 255 255 0 255 255 0
0 0 0 0 255 255 255 255 255 255 0 255 0
0 0 0 255 255 255 255 255 255 255 0 255 0
0 0 255 255 255 255 255 255 255 255 255 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0
3.2.4. Индексированные (сжатые) изображения(indexed colormap)
MATLAB имеет собственный формат представления цветных изображений, который используется в командах обработки изображений, будем называть его в дальнейшем индексированным. Этот способ предстваления изображения сжимает RGB информацию, при этом качество изображения теряется, но скорость обработки информации о цвете возрастает.
Конструкция индексированного файла состоит в следующем. Стандартное цветное изображение сопоставляет каждому (i,j) пикселу тройку значений (R(i,j), G(i,j), B(i,j)). Так как значения всех координат - целые числа из интервала  то различных комбинаций – конечное число – не более 2563. Величины интенсивностей R(i,j), G(i,j), B(i,j) нормируются и отображаются на отрезок [0,1].
то различных комбинаций – конечное число – не более 2563. Величины интенсивностей R(i,j), G(i,j), B(i,j) нормируются и отображаются на отрезок [0,1].
MATLAB создает наборы RGB-троек в виде матрицы Colormap_ k*3, которая имеет 3 столбца и m строки. По умолчанию m=64. Тогда номер 0<k<m-1 для каждого пиксела дает тройку цветов. Таким образом, индексированный формат – это матрица K(i,j), где для (i,j) пиксела указано значение k - номер строки в матрице Colormap.
Объект colormap задает цветовую аппроксимацию изображения и строится следующим образом. Каждая RGB координата из отрезка [0,255] пропорционально отображается в [0,1]. Определяется минимальное и максимальное значение каждой координаты, каждый отрезок изменения координат разбивается на 4 части. Рассматриваются все тройки с такими координатами. Количество всех вариантов 43 =64, поэтому m=64. Затем все тройки выписываются в лексико-графическом порядке в предположении, что B –младший разряд, а R – старший.
При конвертировании изображения типа true color в индексированный формат с матрицей colormap цвет (R(i,j), G(i,j), B(i,j)) каждого пиксела заменяется на наиболее близкую в норме l2 тройку из списка colormap.
Пример 3.4.Пример индексированного формата цветного изображения приведен на рис.7 .
Рассмотрим простейший графический файл из 9-ти пикселов, цвет которых по периметру белый и цвет пиксела в центре – черный.

Рис.7. 9 пикселов
Тогда RGB структура изображения имеет вид:
| A(:,:,1) = 255 255 255 255 0 255 255 255 255 | A(:,:,2) = 255 255 255 255 0 255 255 255 255 | A(:,:,3) = 255 255 255 255 0 255 255 255 255 |
Индексированный формат – это матрица map и матрица индексов.
>> map=colormap
map =
N R G B
1 0 0 .5625
2 0 0 .6250
3 0 0 0.6875
4 0 0 0.7500
5 0 0 0.8125
6 0 0 0.8750
7 0 0 0.9375
8 0 0 1.0000
9 0 0.0625 1.0000
10 0 0.1250 1.0000
11 0 0.1875 1.0000
12 0 0.2500 1.0000
13 0 0.3125 1.0000
14 0 0.3750 1.0000
15 0 0.4375 1.0000
16 0 0.5000 1.0000
17 0 0.5625 1.0000
18 0 0.6250 1.0000
19 0 0.6875 1.0000
20 0 0.7500 1.0000
21 0 0.8125 1.0000
22 0 0.8750 1.0000
23 0 0.9375 1.0000
24 0 1.0000 1.0000
25 0.0625 1.0000 0.9375
26 0.1250 1.0000 0.8750
27 0.1875 1.0000 0.8125
28 0.2500 1.0000 0.7500
29 0.3125 1.0000 0.6875
30 0.3750 1.0000 0.6250
31 0.4375 1.0000 0.5625
32 0.5000 1.0000 0.5000
33 0.5625 1.0000 0.4375
34 0.6250 1.0000 0.3750
35 0.6875 1.0000 0.3125
36 0.7500 1.0000 0.2500
37 0.8125 1.0000 0.1875
38 0.8750 1.0000 0.1250
39 0.9375 1.0000 0.0625
40 1.0000 1.0000 0
41 1.0000 0.9375 0
42 1.0000 0.8750 0
43 1.0000 0.8125 0
44 1.0000 0.7500 0
45 1.0000 0.6875 0
46 1.0000 0.6250 0
47 1.0000 0.5625 0
48 1.0000 0.5000 0
49 1.0000 0.4375 0
50 1.0000 0.3750 0
51 1.0000 0.3125 0
52 1.0000 0.2500 0
53 1.0000 0.1875 0
54 1.0000 0.1250 0
55 1.0000 0.0625 0
56 1.0000 0 0
57 0.9375 0 0
58 0.8750 0 0
59 0.8125 0 0
60 0.7500 0 0
61 0.6875 0 0
62 0.6250 0 0
63 0.5625 0 0
64 0.5000 0 0
>> B=rgb2ind(A,map) % представление изображения на % Рис.4 в индексированном
% формате.
B =
31 31 31
31 63 31
31 31 31
Пример 3.5.Рассмотрим цветное изображение (рис.8) и результат его преобразования в индексированный формат со значениями m=64 и m=8.

Рис.8. Цветное изображение в формате RGB
Выполним последовательность команд
>> I=imread(‘RGB.jpg’);
>> [II,map] = rgb2ind(I,64);
>> imshow(II,map)
>> [II,map] = rgb2ind(I,8);
>> imshow(II,map)
 |  |
| Рис.9. Индексированный формат при m=64 | Рис.10. Индексированный формат при m=8 |
В случае m=8 объект colormap имеет вид:
>> map
map =
0.2196 0.2784 0.2039
0.6471 0.7216 0.6863
0.4196 0.4784 0.3765
0.1529 0.4392 0.6510
0.4275 0.4902 0.4863
0.8824 0.9059 0.8745
0.3451 0.4039 0.2667
0.5059 0.5765 0.5373
На рис.9 и 10 можно наблюдать снижение качества изобра-жения при убывании m.
Загрузка графического файла
Для загрузки графического файла используется функция imread:
>> I=imread('d:\МВ\book_2007\1\0\фото\light.jpg');
Параметром функции является полное имя графического файла, указанное в апострофах. Информация считывается и присваивается переменной I.
Вывод изображения на экран
Отобразить на экран прочитанное изображение можно с помощью команды:
>> imshow(I)
Появится графическое окно с именем Figure1 и в нем отразится изображение (Рис.7)

Рис.7. Вывод изображения на экран
Поворот изображения
Обработка матрицы изображения осуществляется по строкам или столбцам, что накладывает некоторые ограничения при анализе симметричности объекта. Поэтому в некоторых приложениях важно иметь возможность поворота объекта в плоскости как целого. Для этой цели используется функция imrotate.
Команда imrotate(Im, a, s) выполняет поворот изображения на угол a, s - метод интерполяции. Можно использовать три метода: «’nearest’»-интерполяция по цвету ближайших пикселов, «’bilinear’»-билинейная интерполяция, «’bicubic’»-бикубическая интерполяция. Если параметр s не указан, по умолчанию используется 'nearest'.
Пример 3.3.
>>Imrotate = imrotate(Im,45, 'bicubic');
% Поворот изображения Im на 45
% градусов с бикубической
% интерполяцией
>>imshow(Imrotate)

Рис.9. Исходное изображение Im

Рис.10. Результат поворота на 45 градусов
Упражнение 3.1.Глубиной фрагмента изображения называется физическое расстояние до объекта, прообраза. Как оценить глубину изображения?
Упражнение 3.2.Предположим, что точность аппроксимации изображения - один пиксель. Какова относительная ошибка аппроксимации объектов на изображении в зависимости от глубины?
Упражнение 3.3.Почему при определенных скоростных режимах крутящегося колеса телеги наблюдается как бы схема направления вращения?
Упражнение 3.4.Как меняется форма наблюдаемого объекта на изображении в зависимости от скорости перемещения объекта?
Программирование в MATLAB
Внешние текстовые файлы
Изображение является внешним графическим файлом по отношению к пакету MATLAB, т.е. файлом, полученным независимым от MATLAB способом, например, с помощью фотокамеры. Естественно, что такие графические файлы доступны для обработки и другими программными приложениями. Получив матрицы цветов изображения с помощью MATLAB, бывает полезно сохранить эти числовые данные в виде текстового файла, который может использоваться другими приложениями. С другой стороны может возникнуть потребность прочитать текстовую информацию, полученную в других приложениях. Такие файлы называются внешними текстовыми файлами (по отношению к среде MATLAB).
MATLAB имеет функции работы с внешними файлами, аналогичные стандартным алгоритмическим языкам, таким как Pasсal и C++, например, assignfile(f), closefile(f).
Пример 4.1. Записать строку «12345.» в текстовый файл data.txt.
>> fid = fopen('C:\temp\data.txt','w');
% открытие файла на запись данных
>> fprintf(fid,'12345.\n');
% запись строки символов в файл
>> fclose(fid); % закрытие файла
>> open('C:\temp\data.txt');
% открытие файл в текстовом редакторе
Работа с m-файлами
MATLAB позволяет создавать собственные функции – группы команд, которые можно использовать также как стандартные. Это процедуры, которые хранятся в файлах с расширением m - *.m. Необходимо создать группу команд, выделить входные и выходные параметры, дать им имена. Функции, задаваемые в m-файлах имеют следующую структуру: заголовок функции, h1 – строка - текст справки, тело функции, комментарии.
function имя(х1, х2,…..хn) % комментарий
y1=command 1(х1,х2,….хn)
……….
yk=command 1(х1,х2,….хn)
end
Здесь х1, х2,…,хn – входные параметры; y1,…, yn– выходные, имя – идентификатор новой функции. Файл записывается в текстовом редакторе и сохраняется под именем, совпадающим с идентификатором функции, с расширением *.m. Затем функцию можно вызвать в командной строке после системного приглашения.
Замечание. Для того, чтобы пользоваться функцией, заданной m-файлом, из рабочей области MATLAB, нужно разместить его в рабочей директории (см. п.1 рис.1.-выбор директории).
Пример 4.4. Задано цветное изображение объекта на почти однородном фоне. Требуется перевести изображение в бинарный формат так, чтобы белый цвет соответствовал фону, а черный - объекту.
Создадим m-файл, который решает задачу для любого изображения. Применим следующий алгоритм. Переведем цветное изображение в полутоновый формат. Вычислим среднее значение интенсивности. Применим бинаризацию с порогом, равным этому среднему значению.
Входным параметром является имя графического файла изображения - szFileName.
Код m-файла bindiff.m:
function bindiff (szFileName)
warning off all
img = imread(szFileName);
% чтение изображения
grayImage = rgb2gray( img );
% перевод GRB
% изображения в полутоновое
lines= size(grayImage, 1);
% определение числа строк
cols=size(grayImage, 2);
% определение числа столбцов
iTotalPixels = lines*cols;
BorderCount = 30;
BorderPrior = 100;
avgcolor=uint32(0);
koef = uint32(0);
for i=1:lines%Цикл по числу строк
for j=1:cols%Цикл по числу столбцов
if ( i<BorderCount | j<BorderCount | lines-i<BorderCount | cols-j<BorderCount)
koef = BorderPrior;
else
koef = 0;
end
avgcolor=avgcolor+(koef+1)*uint32(grayImage(i,j));
iTotalPixels=iTotalPixels + koef;
end; %конец цикла по столбцам
end; %конец цикла по строкам
% вычисление среднего цвета
% изображения
avgColor=double(avgcolor)/double(iTotalPixels);
diffparam=avgColor/3;
%Вычисление порога %бинаризации
res=logical( grayImage );
%Инициализация бинарного
%изображения, в которое будет
%записан результат
for i = 1:lines %Цикл по числу строк
for j=1:cols %Цикл по числу столбцов
if(abs(double(grayImage(i,j))- double(avgColor)) < double(diffparam))
res(i,j)=1; % белый
else
res(i,j)=0; % черный
end %конец цикла по столбцам
end %конец цикла по строкам
imshow(res);% вывод преобразованного
% изображения на экран
End % конец функции
Обращение
>> bindiff(‘filename.jpg’);
 |  |
| Рис.3. Исходное изображение | Рис.4. Результат работы программы bindiff |
Пример m-файла. Умножение изображений
Пусть на заданном изображении необходимо проанализировать выделенную область, например, квадрат. Создадим вспомогательный графический бинарный файл необходимого размера, на котором нужная область имеет белый цвет, а игнорируемое дополнение – черный. Тогда матрица такого файла - характеристическая функция области. Умножив попиксельно эти два изображения, получим новое, в котором игнорируемые пикселы будут черного цвета.
Реализовать это действие можно с помощью следующего m-файла:
function IJ=umnozhenie(way1,way2)
warning off all
I1=imread( way1 );
J1=imread( way2 );
IJ=immultiply(I1,J1);
imshow(I1),figure,imshow(J1),figure,imshow(IJ);
end
Пример 4.5. Применить вышеприведенный m-файл к следующим изображениям:
 |  |
| Im1.bmp | Im2.bmp |
>> umnozhenie(‘Im1.bmp’, ‘Im2.bmp’)

Рис. 5. Результат применения функции umnozhenie
к Im1.bmp и Im2.bmp
Замечание.Для выполнения операций над матрицами двух изображений применяются также следующие процедуры:
Imabsdiff - вычисление модуля разности интенсивностей двух изображений;
imadd - сложить два изображения ;
imcomplement – найти дополнительное (негативное) изображение;
imdivide - разделить одно изображение на другое;
imlincomb - вычислить линейную комбинацию изображений; imsubtract - вычесть одно изображение из другого.
Команда Plot
Требуется построить график функции y=f(x) для х 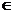 [a,b]. Эту задачу решает команда plot, которая может быть использована в одном из следующих видов:
[a,b]. Эту задачу решает команда plot, которая может быть использована в одном из следующих видов:
1) plot(y) % построение графика значений вектора y;
2) plot(x, y) % построение графика y(x), где x и
% y – векторы одного размера;
3) plot(x, y, s) % то же самое, параметр s задает стиль
% графического вывода;
4) plot(x1, y1, s1, x2, y2, s2, ...)
% построение нескольких графиков
% в одном окне.
Пусть параметр х принадлежит отрезку [a,b]. Зададим равномерное разбиение отрезка на n частей с шагом h. Тогда использование функции plot может быть построено следующим образом.
Пример 5.1. Пусть 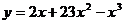 ,
, 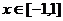 . Положим n=20. Тогда
. Положим n=20. Тогда 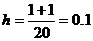
Построение графика в MATLAB будет выполнено с помощью следующих команд:
>>i=1:20; % Ввод индексов точек разбиения
>>h=0.1;
>>x=-1+i+h % Вычисление вектора х – точек
% разбиения отрезка [-1,1]
>>y=2*x+23*x.^2-x.^3 % Вычисление вектора у –
% значения в точках х
>>plot(y) % График функции y(i)
>>plot(x,y) % График функции y(x)
Результат показан на рис. 1.
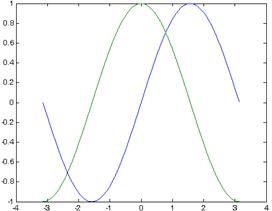
Пример 5.2. Требуется построить графики двух функций — sin(x) и cos(x) на отрезке [-p,p ] . Результат показан на рис 2.
Используем вариант команды plot(x, y), при котором значения выводимых функций содержатся в матрице y, а значения аргумента х хранятся в векторе x. При этом значения одной функции должны находиться в первом столбце, а второй функции – во втором.
>> x=-pi:pi/500:pi; % Вектор-строка аргументов
>> y1=sin(x); %Вектор-строка значений
% функции sin(x);
>> y2=cos(x); % Вектор-строка значений
% функции cos(x);
>> plot(x,[y1',y2']) % Вывод графика двух
% функций.
% Обратить внимание на
% необходимый символ “ ’ ”
 | |||
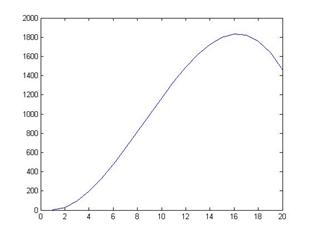 | |||
Рис. 1. График Рис. 2. График
функции y(i) из функций sin(x), cos(x)
примера 5.1 из примера 5.2
5.2. Настройка параметров графического вывода команды plot
Если требуется изменить тип линий или их цвет, в списке аргументов plot добавляется параметр s: plot(x, y, s). Это строковая переменная, которая позволяет задать способ отображения линии, способ отображения точек, цвет линий и точек. Список значений переменной s, которая может быть составлена комбинацией до трех параметров, приведен в следующей таблице.
| Тип линии | Тип метки | Цвет | ||||||||||||||||||||||||||||||||||
|
|
|
Если цвет линии не указан, он выбирается по умолчанию из шести первых цветов, с желтого до синего, повторяясь циклически.
Команда plot(x1, y1, s1, x2, y2, s2, ...) позволяет объединить в одной координатной системе (одном окне) несколько графиков функций y1(x1), y2(x2), ..., определив для каждой из них свой способ отображения.
Пример 5.3. Построить графиков тр
