Перевод чисел из одной системы счисления в любую другую онлайн

Калькулятор переводит числа из одной системы счисления в любую другую.
Он может переводить числа из двоичной в десятичную или из десятичной в шестнадцатеричную, показывая подробный ход решения.
Вы с легкостью можете перевести число из троичной в пятеричную или даже из семеричной в семнадцатеричную.
Калькулятор умеет переводить числа из любой системы счисления в любую другую.

Примечание 3. Решение задач

http://distan-school.ru/ege/?tap=3HYPERLINK "http://distan-school.ru/ege/?tap=3&var=12"&HYPERLINK "http://distan-school.ru/ege/?tap=3&var=12"var=12

№ 1

Сколько значащих нулей в двоичной записи шестнадцатеричного числа 1D2E3₁₆?

Решение

• Так как 2-ная и 16-ричная системы счисления являются взаимосвязанными (число 16 является степенью числа 2), то можно построить таблицу соответствия 16-ричных цифр и двоичных.

• При построении таблицы нужно учитывать, что на одну шестнадцатиричную цифру приходится 4 двоичные (16 = 2⁴)

16-ричная цифра	двоичный код		16-ричная цифра	двоичный код
			A
			B
			C
			D
			E
			F

• Переведем число в 2-ную систему счисления:

1D2E3₁₆ = 0001 1101 0010 1110 0011₂

• Вывод: количество значащих нулей = 7

Ответ: 7

№ 2

Логическая функция F задаётся выражением F = x ∧ (z) ∨ (x) ∧ y ∧ z.

. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c?

Перем. 1	Перем. 2	Перем. 3	Функция
???	???	???	F

В ответе напишите буквы х, у, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и таблица истинности:

перем.1	перем.2	Функция
???	???	F

Тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.

Ответ запишите МАЛЕНЬКИМИ ЛАТИНСКИМИ буквами.

Решение

• Построим логическое выражение по таблице истинности, обозначив переменные новыми незанятыми буквами, например, a, b, c:

Перем. 1	Перем. 2	Перем. 3	Функция
a	b	c	F
				a*b*c (т.к. a=0, c=0 берем их отрицание)
				a*b*c (т.к. a=0 берем его отрицание)
				a*b*c

• Сложим полученные выражения и сократим формулу:

F = a*b*c + a*b*c + a*b*c = a*b+ a*b*c

• Сравним полученную формулу с исходным выражением:

F = x ∧ (z) ∨ (x) ∧ y ∧ z

F = a*b+ a*b*c

• Вывод: z - это а, x - это b, а оставшаяся переменная y - это c.

Ответ: zxy

№ 3

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).

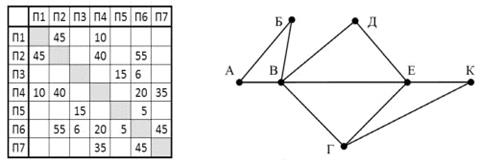
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Г.

В ответе запишите целое число – так, как оно указано в таблице.

• Есть только одна вершина с пятью дорогами - это В, в таблице - это П6.

• Есть только одна вершина с четырьмя дорогами - это Е, в таблице - П4.

• Есть только одна вершина с тремя дорогами - это Г, в таблице - П2.

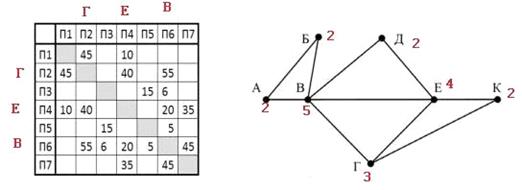
• Вывод: длина пути ВГ равна 55.

Ответ: 55

№ 4

В фрагменте базы данных представлены сведения о родственных отношениях. На основании приведённых данных определите, ID племянника Ерёма А. И.

Племянником считается сын брата или сестры.

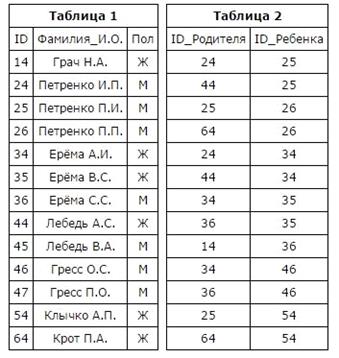
Решение

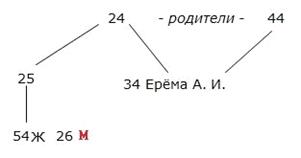
Ответ: 26

№ 5

Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется неравномерный (по длине) код: А-10, Б-11, В-001, Г-011. Через канал связи передается сообщение: АБГВГБ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в шестнадцатеричный код.

В ответе используйте заглавные буквы, систему счисления указывать не нужно.

• АБГВГБ = 10 11 011 001 011 11₂ = 0101 1011 0010 1111₂ = 5B2F₁₆

Ответ: 5B2F

№ 6

На экране есть два окна, в каждом из которых записано по числу. Исполнитель СУММАТОР имеет только две команды, которым присвоены номера:

1. Запиши сумму чисел в первое окно
2. Запиши сумму чисел во второе окно

Напишите программу, содержащую не более 5 команд, которая из пары чисел 1 и 2 получает пару чисел 13 и 4.

В ответе укажите только номера команд

• Сначала получим число 4 в одном окне (т.к. оно самое маленькое), а потом получим число 13 в другом окне:

1,2 → 1,3 → 1,4 → 5,4 → 9,4 → 13,4

• Вывод: порядок команд 22111

Ответ: 22111

№ 7

Дан фрагмент электронной таблицы.

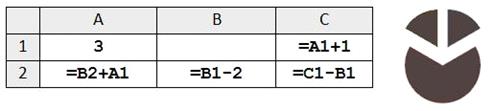
Какое целое число должно быть записано в ячейке B1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

• Проанализируем полученную диаграмму: две ячейки равны между собой, а третья ячейка намного больше.

• В таблице:

• A2 = x+3

• B2 = x-2

• C2 = 4-x

• Вывод: значение в ячейке A2 больше значения в ячейке В2, значит, В2 и С2 - это равные между собой ячейки

x-2 = 4-x

2х = 6

х = 3

Ответ: 3

№ 8

Определите, что будет напечатано в результате работы следующего фрагмента программы:

• Цикл while выполняется до тех пор, пока k<30 , т. е. как только k станет ≥ 30 цикл закончится и программа выведет результат.

• В цикле переменная k увеличивается на 3, а до цикла её значение было равно 0. Следовательно, количество повторений в цикле равно 30/3=10

• После 10 шага цикла переменная s станет равна:

s = (((((((((0+3)+6)+9)+12)+15)+18)+21)+24)+27)+30 = 165

Ответ: 165

№ 9

После преобразования растрового 256-цветного графического файла в черно-белый формат (2 цвета) его размер уменьшился на 7 Кбайт. Каков был размер исходного файла в Кбайтах?

В ответе запишите только целое число, единицу измерения писать не нужно

I = w*h*i

w*h - размеры изображения в пикселах

i - минимальный объем памяти в битах для кодирования 1 цвета (пиксела)

N = 2ⁱ

N - количество цветов в палитре

• Пусть N₁ - количество цветов в исходном файле, а N₂ - количетсов цветов в преобразованном файле

N₁=256 => i₁=8 бит

N₂=2 => i₂=1 бит

I₁ - I₂ = 7 Кб

w*h*i₁ - w*h*i₂ = 7 Кб

8wh-1wh=7*2¹³ бит

wh = 2¹³

I₁ = w*h*i₁ = 2¹³ * 8 бит = 8 Кб

Ответ: 8

№ 10

Все 5-буквенные слова, составленные из букв А, К, Р, У, записаны в алфавитном порядке. Вот начало списка:

• ААААА

• ААААК

• ААААР

• ААААУ

• АААКА

...

Запишите слово, которое стоит на 250-м месте от начала списка.

В ответе используйте заглавные русские буквы, без пробелов

Решение

• Пусть А=0, К=1, Р=2, У=3, тогда список примет вид:

• 00000

• 00001

• 00002

• 00003

• 00010

• ...

• Это цисла в 4-ной системе счисления. Слово, которое находится на 250-м месте равно числу (250-1) в 4-ной системе счисления:

• Переведем 249 в 4-ную систему счисления: 249 = 3321₄ (недостающие разряды дописываем незначащами нулями)

• 03321 = АУУРК

Ответ: АУУРК

№ 11

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = F(n–1) + 2^n–1 , если n > 1.

Чему равно значение функции F(12)?

Решение

• Построим дерево рекурсивных вызовов:

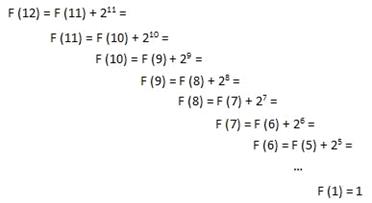
• Следовательно, F(12) = 2¹¹ + 2¹⁰ + 2⁹ + 2⁸ + 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 1 = 4095

Ответ: 4095

№ 12

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, – в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда – нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Два узла, находящиеся в одной сети, имеют IP-адреса 211.115.61.154 и 211.115.59.137. Укажите наибольшее возможное значение третьего слева байта маски сети.

Ответ запишите в виде десятичного числа.

Решение

• Переведём в двоичную систему третие слава байты обоих ip-адресов:

61 = 32+16+8+4+1 = 111101₂ = 001 11101₂

59 = 32+16+8+2+1 = 0011 1011₂

• Сравним полученные числа: до тех пор, пока биты в обоих ip-адресах совпадают, в маске сети могут стоять единицы:

маска

• Вывод: у данных ip-адресов есть 5 совпадений (смотрим слева), значит в маске сети третий байт может быть равен 11111000₂ = 248 (это наибольшее возмлжное значение)

Ответ: 248

№ 13

Два сторожевых отряда, расположенных на большом расстоянии друг от друга, условились передавать друг другу сообщения при помощи сигнальных ракет красного и зеленого цвета. Сколько различных сообщений можно передать таким способом, запустив только 3 ракеты?

В ответе запишите только целое число, единицу измерения писать не нужно

Решение

N = 2ⁱ

2 - так как только два цвета ракет

i = 3 , т.к. запусить можно только 3 ракеты

N - количество сообщений

N = 2³ = 8

Ответ: 8

№ 14

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27) преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.

В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (333) ИЛИ нашлось (777)
ЕСЛИ нашлось (777)
ТО заменить (777, 3)
ИНАЧЕ заменить (333, 7)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 156 идущих подряд цифр 7?

Решение

• Проработаем алгоритм для исходной строки:

7₍₁₅₆₎ → 3₍₅₂₎ Т.е. строка из одних семерок станет строкой из одних троек

• Проработаем алгоритм для новой строки:

3₍₅₂₎ → 7₍₃₎3₍₄₃₎ → 3₍₄₄₎ Т.е. строка из одних троек уменьшится на 8 троек, новых цифр не появится. 1 полных цикл равен -8 троек

44/8 = 5 "полных циклов" и 4 в остатке

• Проработаем алгоритм для остатка:

3333 → 73

Ответ: 73

№ 15

На рисунке показана схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город М?

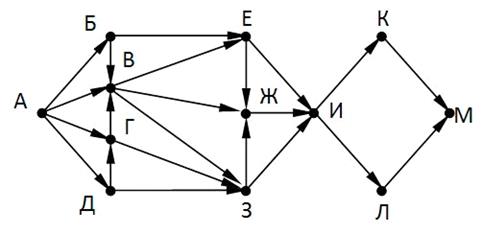
Решение

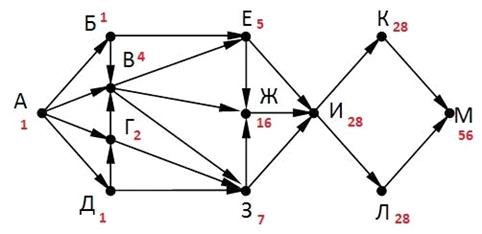
Ответ: 56

№ 16

Сколько единиц содержится в двоичной записи значения выражения: 4²⁰²⁰ + 2²⁰¹⁷ – 15?

Решение

• Переведем все числа в 2-ную систему счисления:

• Для удобства, представим число 4 как 2² , следовательно, 4²⁰²⁰ = (2²)²⁰²⁰ = 2⁴⁰⁴⁰

• Число 2 в 2-ной системе счисления = 10₂

• Перепишем выражение в 2-ной системе счисления:

10⁴⁰⁴⁰ + 10²⁰¹⁷ – 1111?

• Результат выражения 10⁴⁰⁴⁰ + 10²⁰¹⁷ будет выглядить следующим образом:

номер разряда:	4040	4039	...	2018	2017	2016	...	4	3	2	1	0	Т.е. результатом будет число в котором на месте 4040-го и 4039-го разряда стоят единицы.
результат:			...				...

• Вычтем из полученного числа 1111:

номер разряда:	4040	4039	...	2018	2017	2016	...	4	3	2	1	0	Т.е. результатом будет число в котором с 4-го по 2016-й разряд стоят единицы, а также 0-й разряд и 4040-й равен 1.
104040+102017			...				...
							...
результат:			...				...

• Вывод: 2016-4+1+2=2015

Ответ: 2015

№ 17

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

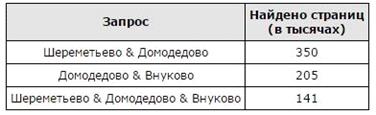
Какое количество страниц (в тысячах) будет найдено по запросу (Шереметьево & Домодедово) | (Внуково & Домодедово) ?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

решение

• Выделим цветом искомую область:

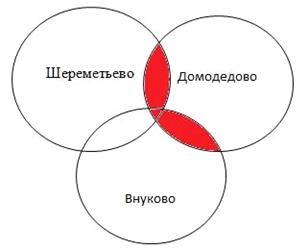
• Вывод: (Шереметьево & Домодедово) | (Внуково & Домодедово) = 350+205-141 = 414

Ответ: 414

№ 18

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110 2 &0101 2 = 0100 2 = 4.

Определите наименьшее натуральное число A, такое что выражение

(X & 56 ≠ 0) → ((X & 48 = 0) → (X & A ≠ 0))

тождественно истинно?

Решение

• Заменим все имплекации на простые логические операции (отрицание и дизъюнкция) по формуле A→B = A + B

(X & 56 ≠ 0) → ((X & 48 = 0) → (X & A ≠ 0))

(X & 56 = 0) + (X & 48 ≠ 0) + (X & A ≠ 0)

• Рассмотрим первое слагаемое (x&56= 0): для каких чисел х это слагаемое даёт ИСТИНУ:

а) Переведём число 56 в 2-ную систему счисления

56 = 111000₂

б) Проанализируем результат поразрядной конъюнкции с числом 111000₂ :

разряды=	+∞	...	5	4	3	2	1	0	Пронумеруем разряды в числе. Если в числе х на месте 0-го, 3-го, 4-го и 5-го разряда окажутся единицы, то после поразрядной конъюнкции на этих местах также будут стоять единицы, т.е.мы не получим "0" и выражение (x&56 = 0) будет ЛОЖНО.
25=		...
х=		...
результат=		...

Все остальные цифры в числе х могут быть любыми, так как после поразрядной конъюнкции на этих местах все равно будет "0".

в) Вывод: первое слагаемое учитывает все числа х, в которых нет на 0-м, 3-м, 4-м и 5-м местах единиц.

• Рассмотрим второе слагаемое (x&48 ≠ 0): только для тех чисел х, у которых на 0-м, 3-м и 4-м местах стоят единицы:

а) Переведём число 48 в 2-ную систему счисления

48 = 110000₂

б) Проанализируем результат поразрядной конъюнкции с числом 10001₂ :

разряды=	+∞	...				2	1		Пронумеруем разряды в числе. Если в числе х на месте 3-го разряда стоит единица, то после поразрядной конъюнкции на этом месте будут стоять ноль, т.е. мы не получим "1" и выражение (x&48 ≠ 0) будет ЛОЖНО.
48=		...
х=		...
результат=		...

Единицы на 0-м, 4-м и 5-м месте в числе х после поразрядной конъюнкции адут "1" и выражение (x&48 ≠ 0) будет ИСТИННО.

в) Вывод: второе слагаемое учитывает числа х, в которых на 0-м и 4-м местах стоят "1" и не учитывает числа х, в которых на 3-м месте стоит "1".

• Рассмотрим третье слагаемое (x&A≠0):

У нас остались неучтенными лишь те числа х, у которых на 3-м месте стоит "1", следовательно, их нужно учесть в числе А. Минимально возможное такое число это 1000₂ = 8

Ответ: 8

№ 19

Значения элементов двухмерного массива A[1..10,1..10] сначала равны 5. Затем выполняется следующий фрагмент программы:

Сколько элементов массива будут равны 10?

Решение

• Представим элементы массива в виде таблицы:

• Выполним первый шаг цикла: i=1, j=1 (так как i=j, поменяется только одна ячейка в массиве):

• Выполним вложенный цикл для j полностью, при i=1:

• Выполним вложенный цикл для j полностью, при i=2:

• Выполним вложенный цикл для j полностью, при i=3:

• Выполним вложенный цикл для j полностью, при i=4:

• Выполним вложенный цикл для j полностью, при i=5:

• Вывод: 8 ячеек равны 10

Ответ: 8

№ 20

Ниже записан алгоритм. Сколько существует таких чисел x, при вводе которых алгоритм печатает сначала 2, а потом 12?

• Алгоритм печатает сначала 2, а потом 15. Значит после выполнения алгоритма a=2, b=12

• Переменная а до цикла была равна 0, а в цикле увеличивалась на 1, следовательно, цикл был выполнен всего два раза.

• Цикл выполняется до тех пор, пока x>0 , а в самом цикле переменная x уменьшается в 100 раз (убирается последняя цифра в числе), следовательно, число х могло быть четырёхзначным.

• Переменная b в цикле меняется так: b:=b + (x mod 100)

b получается в результате сложения двухзначных чисел, полученных из числа х.

Так как b = 12, то можно разложить это число: 12+0, 11+1, 10+2, 9+3, 8+4, 7+5, 6+6

• Всего можно составить 12 чисел: 1200, 1101, 111, 1002, 210, 903, 309, 804, 408, 705, 507, 606

Ответ: 12

№ 21

При каком наибольшем значении входной переменной k программа выдаёт тот же ответ, что и при входном значении k = 60?

Решение

• Программа выполняет действия в цикле до тех пор, пока F(i) ≥ k и i>i, т.е. как только i≤0 или F(i) < k программа закончит выполнять цикл.

• Вычислим F(15):

F(15) = 2*225-30 (> 60)

• Найдем значение i, при котором программа выйдет из цикла и напечатает результат:

F(n)<k

2*n*n-30<60

2*n2<90

n2<45

n<6 (максимальное положительное число, при котором n2<45)

• Следовательно, при вводе числа 60, на экране будет напечатан результат: 6

• Найдем наибольшее входное значение k, при котором на экране также будет напечатан результат 6:

Для этого вычислим F(7):

F(7) = 68

Ответ: 68

№ 22

У исполнителя Удвоитель-Утроитель три команды, которым присвоены номера:

• прибавь 1

• умножь на 2

• умножь на 3

Первая из них увеличивает на 1 число на экране, вторая увеличивает это число в 2 раза, третья - в 3 раза. Сколько существует программ, которые число 1 преобразуют в число 13?

решение

• Все числа, большие 6 имеют только один способ получения числа 13 (с помощью команды "+1")

• Рассмотрим числа ≤ 6:

6: "*2"=12 (1 способ) или "+1"=7 (1 способ) Итого: 2

5: "*2"=10 (1 способ) или "+1"=6 (2 способа) Итого: 3

4: "*3"=12 (1 способ) или "*2"=8 (1 способ) или "+1"=5 (3 способа) Итого: 5

3: "*3"=9 (1 способ) или "*2"=6 (2 способа) или "+1"=4 (5 способов) Итого: 8

2: "*3"=6 (2 способа) или "*2"=4 (5 способов) или "+1"=3 (8 способов) Итого: 15

1: "*3"=3 (8 способов) или "*2"=2 (15 способов) или "+1"=2 (15 способов) Итого: 38

Ответ: 38

№ 23

Сколько существует различных наборов значений логических переменных x₁, x₂, ... x₇, y₁, y₂, ... y₇, которые удовлетворяют всем перечисленным ниже условиям?

(x₁ ∧ y₁) ≡ (x₂ ∨ y₂)
(x₂ ∧ y₂) ≡ (x₃ ∨ y₃)
...
(x₆ ∧ y₆) ≡ (x₇ ∨ y₇)

Решение

• Применив правило де-Моргана получим следующую систему уравнений:

(x₁ * y₁) ≡ (x₂ * y₂)
(x₂ * y₂) ≡ (x₃ * y₃)
...
(x₆ * y₆) ≡ (x₇ * y₇)

• Введем замены:

z₁=(x₁ * y₁)
...
z₇=(x₇ * y₇)

• Тогда вся система примет вид:

z₁=z₂
...
z₆=z₇

или можно переписать в виде 1 уравнения: (z₁≠z₂)*(z₂≠z₃)*(z₃≠z₄)*(z₄≠z₅)*(z₅≠z₆)*(z₆≠z₇)=1

• Существует только два набора z для данного уравнения: {0101010} или {1010101}

• Пусть z_i = 1, тогда x_i*y_i=1 (1 набор: х_i=1 и y_i=1)

• Пусть z_i = 0, тогда x_i*y_i=0 (3 набора: {00},{01},{10})

• Итого: для z={0101010} количество решений равно 3*1*3*1*3*1*3=81

• Итого: для z={1010101} количество решений равно 1*3*1*3*1*3*1=27

• Всего: 81+27=108 решений

Ответ: 108

№ 24

Даны натуральные числа N и M. Требуется найти такое минимально возможное натуральное число K ≥ N, чтобы сумма всех натуральных чисел от N до K была больше или равна M: N + (N+1) + (N+2) + ... + K ≥ M
Программист написал программу неправильно.

var n, m, sum, k: integer;
begin
read(n,m);
sum := 1;
k := n;
while sum <= m do begin
k := k+1;
sum := sum+k;
end;
writeln(k)
end.

Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе чисел 5 и 8.
2. Приведите пример таких чисел, при вводе которых программа выдаёт верный ответ.
3. Найдите все ошибки в этой программе (их может быть одна или несколько). Известно, что каждая ошибка затрагивает только одну строку и может быть исправлена без изменения других строк. Для каждой ошибки:
1) выпишите строку, в которой сделана ошибка;
2) укажите, как исправить ошибку, т.е. приведите правильный вариант строки.