Энергетические характеристики сигналов

Полная энергия сигнала f может быть записана через амплитуды вейвлет-преобразования в виде:

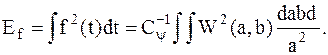
Плотность энергии сигнала 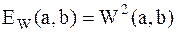- характеризует энергетические уровни исследуемого сигнала f(t) в пространстве (a, b)=(масштаб, время).

Локальный спектр энергии позволяет проанализировать временную динамику передачи энергии процесса по масштабам – обмен энергией между составляющими процесс компонентами разного масштаба в любой заданный момент времени. Зная плотность энергии 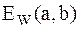, можно с помощью окна определить локальную плотность энергии в точке 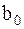(или ):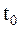

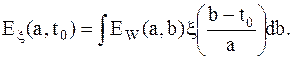
Оконная функция 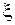«поддерживает» диапазон 0t и удовлетворяет равенству:

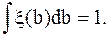
Если в качестве 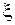выбрать функцию Дирака, то локальный спектр энергии примет вид:

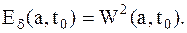
Глобальный спектр энергии. Полная энергия распределена по масштабам в соответствии с глобальным спектром энергии коэффициентов вейвлет-преобразования:

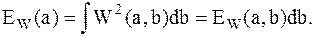
Его называют также скалограммой или дисперсией вейвлет-преобразования.

Мера локальной перемежаемости:

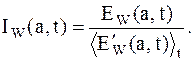
- мера локальных отклонений от среднего поля спектров на каждом масштабе: она позволяет определить степень неравномерности распределения энергии по масштабам (угловыми скобками здесь обозначено усреднение).

Мера контрастности:

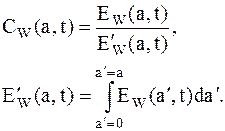
позволяет определять даже самые малые изменения в сигнале, когда необходимо, например, выявить структурированность слабого сигнала или слабые вибрации на фоне крупной структуры.

Вейвлет-анализ сигналов с помощью картин значений коэффициентов вейвлет-преобразований

Картина значений вейвлет-коэффициентов представляет значение коэффициентов вейвлетов в плоскости масштаб (номера коэффициентов) - время (или пространственная координата). Внизу картины значений вейвлет-коэффициентов расположены коэффициенты с малыми номерами, дающие детальную картину сигнала, а сверху - с большими номерами, дающие огрубленную картину сигнала. Результатом вейвлет-анализа заданного сигнала с помощью картин вейвлет-коэффициентов являются графики:

1) график функции заданного сигнала;

2) картины значений вейвлет-коэффициентов;

3) проекции картины значений вейвлет-коэффициентов при фиксированном значении коэффициента a;

4) скелетон (картина линий локальных экстремумов) картины значений коэффициентов вейвлетов.

Для построения картин значений коэффициентов вейвлет­преобразований сигналов используется вычислительный пакет WaveToolbox среды MATLAB, который запускается командой wavemenu. В результате появится окно со списком разделов вейвлет-преобразований (рисунок 3.1).

Для получения справки по какому-либо типу вейвлета при работе в командном режиме MATLAB достаточно исполнить команду waveinfo(‘type’), указав тип вейвлета. Для просмотра же вейвлетов достаточно исполнить команду wavemenu и в появившемся окне со списком разделов ВП нажать кнопку WaveletDisplay. Нажатие этой кнопки выводит окно просмотра вейвлетов, в котором имеется возможность просмотра: общей информации о вейвлетах, выбранного вейвлета (с именем « Name») и информации о нем.

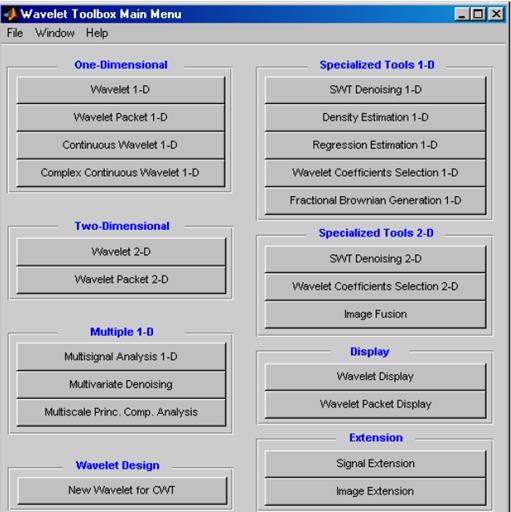
Рисунок 3.1 – Главное меню вычислительного цикла WaveToolbox в Matlab

При вейвлет-анализе заданного сигнала можно использовать набор встроенных вейвлетообразующих функций (на панели справа меню Continuouswavelet 1-D) или задать необходимый вейвлет с помощью инструмента вейвлет-менеджер - wavemngr. Для просмотра встроенных вейвлетов воспользуйтесь кнопкой WaveletDisplay в окне главного меню WaveletToolboxMainMenu.

Для анализа тестовых сигналов с помощью картин значений вейвлет-коэффициентов выберите кнопку главного меню Continuouswavelet 1-D. Появится окно, в котором производится вейвлет-анализ заданного сигнала с помощью непрерывных вейвлетов.

Задания тестовых сигналов производится следующим образом:

Нажмите

• file вменю Continuous wavelet 1-D;

• выберете Loadsignal;

• укажите путь к файлу, в котором задается тестовый сигнал.

Файл с заданным сигналом должен быть сохранен в mat-формате.

В Matlab вейвлет-коэффициенты W(a, b) обозначены С(a, b).

Пример 1. Проведем вейвлет-анализ с помощью картин вейвлет-коэффициентов для сигнала 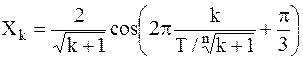, где параметры сигнала k=0, 1, …, 255 на основе вейвлета Хаара.

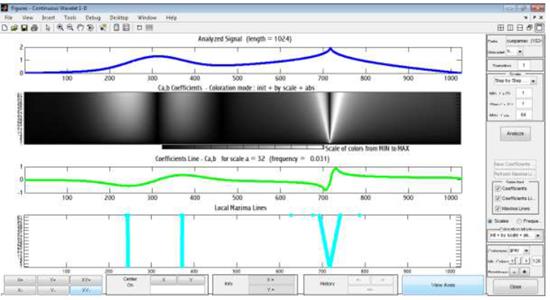
Рисунок 3.2 – Вейвлет-анализ на основе вейвлетообразующей функции Хаара тестового сигнала

Локальным особенностям (нарушениям гладкости) на картине вейвлет-коэффициентов отвечают вертикальные полосы, выходящие из точки, где находится особенность (рисунок 3.2). Пикам сигналов соответствует сгущение светлых областей вейвлет-картин значений коэффициентов, а впадинам сгущение темных полос. Чем резче выражена особенность сигнала, тем сильнее она выделяется на картине значений вейвлет- коэффициентов. Анализ тестовых сигналов с использованием комплексных непрерывных вейвлетов производится в окне главного меню: ComplexContinuouswavelet l-D (рисунок 3.1). Здесь используются два метода анализа заданного сигнала по модулю 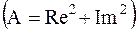и углу 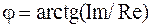, где Im и Re - соответственно мнимая и действительная часть анализируемой функции.

В приводимых ниже примерах прямое ВП реализуется функцией «cwt», которая может быть представлена в нескольких формах, например: COEF=cwt(S, SCALES, «wname» PLOTMODE, XLIM), где строка S-сигнал, строка SKALES - задание диапазона и шага изменения параметра, a строка«wname» - имя (тип) вейвлета, строка PLOTMODE - настройка цвета: «lvl» - окраска шаг за шагом, «glb» - окраска с учетом всех коэффициентов, «absvil» или «lvlabs» - окраска шаг за шагом с использованием абсолютных значений коэффициентов, строка XLIM - строка переменных настройки.

Пример 2. Гармоническое колебание

functiongarm

t=0:0.00001:0.0004; A1=1; F1=10000; a1=45;

s=A1*soc(2*pi*F1*t+a1);

figure (1); plot(t, s); axis([0 0.0004 -3 3]); grid on;

subplot(211), plot(t,s); title ('Сигнал S(t)')

subplot(212), c = cwt(s, 1:2:32, 'mexh', 'abs1vl', [0 10]);

title('Вейвлет-спектр'); xlabel('Временной сдвиг, b'); ylabel('Временной масштаб, a');

end

И хотя спектрограмма гармонического колебания, представленная на рисунок 3.3, особой выразительностью не отличается, на ней отчетливо видны переходы сигнала через нуль (темный тон) и экстремальные точки (светлый тон).

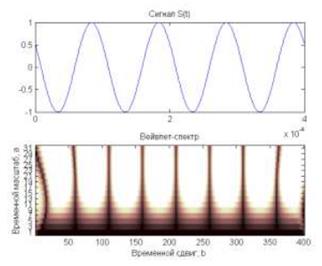
Рисунок 3.3 – Спектрограмма гармонического колебания