Зависимость между координитами точки местности и координатами ее изображения на паре снимков
Получим уравнения связи между координатами точки A местности и координатами ее изображений на паре снимков, исходя из предположения, что элементы ориентирования стереопары известны.
Для решения этой задачи используем в качестве исходной систему координат XYZ с началом в точке фотографирования S1 левого снимка (рис. 38). Вектор  определяет в этой системе положение точки фотографирования S2 правого снимка, а вектора
определяет в этой системе положение точки фотографирования S2 правого снимка, а вектора 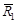 и
и  - положение точек А и ее изображения а1 на левом снимке соответственно. Точки а2 правого снимка и А местности определяют вектора
- положение точек А и ее изображения а1 на левом снимке соответственно. Точки а2 правого снимка и А местности определяют вектора 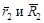 в системе координат S2XYZ. Ее начало находится в точке S2, а оси параллельны соответствующим осям системы координат S1XYZ. Векторы
в системе координат S2XYZ. Ее начало находится в точке S2, а оси параллельны соответствующим осям системы координат S1XYZ. Векторы 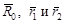 известны, поскольку принято, что элементы ориентирования снимков даны. Искомым является вектор
известны, поскольку принято, что элементы ориентирования снимков даны. Искомым является вектор 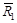 .
.
В силу коллинеарности векторов 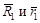 имеем:
имеем:
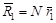 , , | (63) |
где N – скалярный множитель.
Векторы 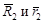 также коллинеарны, поэтому
также коллинеарны, поэтому
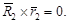
Согласно рис. 38 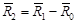 или, с учётом уравнения коллинеарности (63),
или, с учётом уравнения коллинеарности (63), 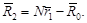 Поэтому можно записать:
Поэтому можно записать:
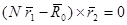
Решая это равенство относительно N, получим
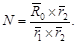 | (64) |
Или, с учетом соотношения (63):
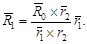 | (65) |
 |
Уравнение (65) - векторное Выразим искомую зависимость в координатной форме.
Векторные произведения векторов 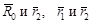 можно представить в виде определителей третьего порядка:
можно представить в виде определителей третьего порядка:
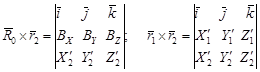 ,
,
где 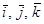 - единичные векторы координатных осей X, Y, Z;
- единичные векторы координатных осей X, Y, Z;
BX, BY, BZ – координаты вектора  , определяющие положение точки фотографирования S2 в системе координат S1XYZ;
, определяющие положение точки фотографирования S2 в системе координат S1XYZ;
X1', Y1', Z1' и X2', Y2', Z2' – пространственные координаты соответственных точек а1 (вектора  ) и а2 (вектора
) и а2 (вектора  ) на первом и втором снимках.
) на первом и втором снимках.
Разложив определители по элементам первых строк, получим:
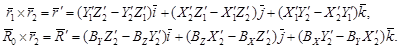
Векторные произведения векторов 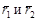 , а также
, а также 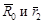 есть вектора
есть вектора 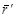 и
и 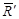 , направленные перпендикулярно к базисной плоскости WA. По этой причине они коллинеарны.
, направленные перпендикулярно к базисной плоскости WA. По этой причине они коллинеарны.
На основании их коллинеарности формулу (64) можно записать в виде следующих пропорций:
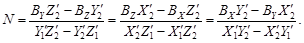 | (66) |
Пространственные координаты X',Y',Z', входящие в уравнения (72), вычисляются по формулам (14-18). Составляющие базиса фотографирования определяются через линейные элементы ориентирования пары снимков:
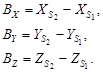 | (67) |
Спроектируем векторы 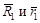 на координатные оси X, Y, Z. Тогда в соответствии с равенством (63) будем иметь:
на координатные оси X, Y, Z. Тогда в соответствии с равенством (63) будем иметь:
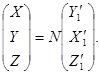 | (68) |
Рассмотренная задача определения пространственных координат точки местности по её изображению на снимках стереопары называется прямой пространственной фотограмметрической засечкой. Ее решение значительно проще для идеальной пары снимков. Случай съемки называется идеальным, если снимки получены с одной и той же высоты фотографирования, а их углы 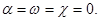 При указанных условиях справедливо:
При указанных условиях справедливо:
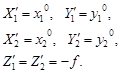 | (69) |
Примем, что ось X совпадает с направлением базиса фотографирования, а ось Y параллельна плоскости снимков. Тогда BZ = BY = 0, BX = B, и из второго отношения пропорции (66) имеем:
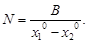 | (70) |
Разность абсцисс p соответственных точек, измеренных на паре снимков, называется продольным параллаксом, т.е.:
p = x1 – x2, или на идеальной паре 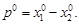 | (71) |
Тогда
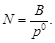 | (72) |
Подставив выражение N из (72) в (68), с учётом (69) получим:
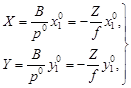 | (73) |
и
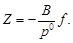 | (74) |
В соотношениях (73) и (74) 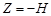 – (высоте фотографирования над точкой местности). Поэтому, согласно формуле (74), параллакс p0 можно определить из соотношения:
– (высоте фотографирования над точкой местности). Поэтому, согласно формуле (74), параллакс p0 можно определить из соотношения:
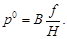 | (75) |
Оно показывает, что продольный параллакс соответственных точек идеальной пары снимков равен базису фотографирования в масштабе снимков.
Формулы (69-75) справедливы и для нормального случая съемки (главные луч перпендикулярны к наклонному базису и взаимно параллельны, а угловые элементы внешнего ориентирования относительно фотограмметрической системы координат равны нулю). При этом предполагается, что ось X совпадаетс базисом, а ось Z - с главным лучом левого снимка.
По паре горизонтальных снимков сравнительно просто решается задача определения превышений точек местности. Примем, что высота точки А местности известна. Тогда превышение точки М над точкой А:
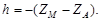 | (76) |
Подставив в (76) для каждой из точек выражение из (74), получим:
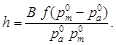
Разность продольных параллаксов 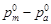 обычно обозначают через
обычно обозначают через 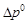 , поэтому, опуская индексы, можно записать:
, поэтому, опуская индексы, можно записать:
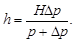 | (77) |
Углы наклона снимков не превышающие 3°, практически не влияют на точность определения превышений между близко расположенными точками. Поэтому формула (77) широко используется для определения высот отдельных объектов и по плановым снимкам (например, деревьев, домов, заводских труб, глубин оврагов и т.д.).
Иногда удовлетворительный результат получается при использовании приближенной формулы:
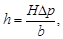 | (78) |
где b – базис фотографирования в масштабе снимка.
Для оценки точности определени превышения продифференцируем функцию (78) по входящим в неё переменным b, Δp, H и перейдём к средним квадратическим ошибкам. В результате получим
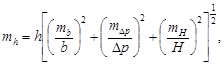 | (79) |
где mh – средняя квадратическая ошибка определения превышений;
mb, mΔp, mH – средние квадратические ошибки определения базиса фотографирования, разности продольных параллаксов и высоты фотографирования соответственно.
На практике влиянием mb и mH пренебрегают, и для оценки используют приближённое соотношение:
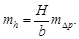 | (80) |
Оно показывает, что величина ошибки mh прямо пропорциональна высоте фотографирования (или фокусному расстоянию АФА, при заданном масштабе аэрофотосъемки) и обратно пропорциональна базису фотографирования.
