Методические указания для выполнения расчетных заданий раздела «биометрия»

Биометрия - наука, представляющая синтез математики и биологии, играет хотя и вспомогательную, но существенную роль в биологических исследованиях (наука о статистическом анализе массовых явлений в биологии). Основная задача биометрии – получение комплекса параметров и коэффициентов, характеризующих членов изучаемой группы животных по одному или нескольким признакам.

Наблюдения над биологическими объектами проводятся по тем или иным признакам, т.е. таким характерным особенностям в строении и функциях живого организма, по которым можно отличить одну единицу наблюдения от другой сравнивать их между собой. Если, исследователя интересует содержание зерен в пшенице (молочная продуктивность коровы), то культура – пшеница (корова) будет объектом исследования, а содержание зерен в колосе (удой) – признаком объекта, который будет рассматриваться как единица наблюдения, составляющая в массе статистическую совокупность, подвергаемую изучению.

Объектом наблюдения служит варьирующий признак, учтенный в группе особей, имеющей достаточную численность. Все биологические признаки варьируют, т.е. изменяются от случая к случаю в определенных пределах.

Варьирование – характерное свойство всего живого. Различные значения варьирующего признака принято называть вариантами.

Все биологические признаки варьируют, но не все поддаются непосредственному измерению. Отсюда следует их деление на качественные и количественные.

Качественные признаки (пол, масть, окраска, тип телосложения, форма гребня у кур, окраска скорлупы, тип движения лошади) контролируются одним или несколькими генами, на действие которых не влияют ненаследственные факторы. Они не поддаются непосредственному измерению и учитывается по наличию их у членов данной совокупности (например в популяции можно учесть количество цветков белой, красной и розовой окрасок и т.п.)

Количественные признаки, мерные (размер колосьев, урожай, удой, яйценоскость и т.п.) представляют большинство хозяйственно-полезных признаков животных по которым ведут селекцию.

Развитие количественных признаков обусловлено большим количеством генов (полигенное наследование), поэтому изучать наследуемость таких признаков труднее. При их изучении приходится сталкиваться с непрерывной изменчивостью. Такая изменчивость количественных признаков, обусловлена действием большого числа генов, так и влиянием факторов внешней среды.

Варьирующие признаки обозначают буквами латинского алфавита – х, y и т.п., а их варианты – х₁, х₂, ….х_n. число особей в выборке – n, генеральной совокупности – N.

Вычисление средних величин

Наблюдения, проводимые над биологическими объектами, могут охватывать всех членов изучаемой совокупности (сплошное наблюдение), а могут ограничиваться обследованием лишь части (выборочное наблюдение). Совокупность из которой отбирается часть – это генеральная совокупность, а отобранная часть – выборка. По выборке судят о состоянии всей генеральной совокупности. Например, нецелесообразно высевать всю партию семян для того, чтобы определить их всхожесть или силу прорастания. Поэтому в большинстве случаев обходятся выборочными наблюдениями (исследованиями).

Количественные показатели (живая масса животных, количество яиц, количество протеина в зерне, удой молока, урожайность зерна и т.п.), которые позволяют судить о качественном своеобразии варьирующих объектов и сравнивать их между собой, называются статистическими характеристиками.

Наиболее важные из них средние величины и показатели вариации признаков.

Средние величины обладают большей устойчивостью, способностью характеризовать группу однородных единиц одним средним числом.

Средняя арифметическая (Х или М) – наиболее распространенный и широко применяемый статистический показатель среднего значения варьирующего признака при количественном его выражении.

Среднюю арифметическую в малочисленных выборках (до 30 особей) вычисляют прямым способом - определяется как сумма всех членов совокупности, делённая на их общее число - n.

Х 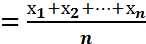,(1)

где х₁, х₂, х_n – члены совокупности.

Х показывает, какое значение признака наиболее характерно в целом для конкретной совокупности животных.

Например, в группе их 10 коров суточный удой молока отдельных особей составил, кг: 18,4; 15,5; 19,1; 14,4; 18,7; 16; 19,5; 17; 20,1; 17,3. Следовательно, средняя арифметическая для группы коров

Х = 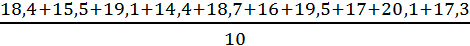= 17,6 кг

Средняя взвешенная (Х_взв) представляет собой результат усреднения средних арифметических нескольких совокупностей. Она вычисляется по формуле:

Х_взв= 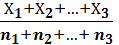= 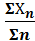, (2)

где Х_взв – средняя взвешенная;

Х₁, Х₂, Х₃…- средние арифметические первой, второй и т.д. совокупностей;

n₁, n₂, n₃ – объем этих совокупностей.

Пример. Требуется вычислить среднюю жирность молока, полученного от коровы за первый квартал, по приведенным ниже данным (табл.1).

Таблица 1 – Данные о содержании жира в молоке и удоях коровы

Месяцы	Средняя жирность молока (Х), %	Удои (n), кг
Январь	4,0
Февраль	3,8
Март	4,0

Средняя взвешенная за квартал равна:

Х_взв = 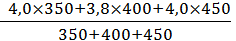= 3,93%