Типы задач, которые будут в экзаменационных билетах.
Типы задач, которые будут в экзаменационных билетах.
1. Задача о двоичных данных.
2. Репрезентативная выборка (с возвращением/без возвращения, однородная/расслоенная ген. совокупность).
3. Однородность выборок. Критерий Вилкоксона.
4. Однофакторный анализ.
5. Независимость признаков. Критерий хи-квадрат.
6. Независимость признаков. Критерии Спирмена и Кендала.
Задача о двоичных данных
Задача 1.1.
Известно, что вероятность рождения мальчика равна 0,52. В случайной выборке из 5000 человек в возрасте от 30 до 60 лет мужчин оказалось 2500. Можно ли считать, основываясь на этих данных, что смертность среди мужчин и женщин одинакова, рискуя ошибиться один раз из 20?
Задача 1.2.
Игральную кость подбросили 600 раз, «пятёрка» выпала 80 раз. На уровне доверия 0,95 проверить гипотезу о том, что кость правильная. Можно ли утверждать на уровне доверия 0,9, что вероятность появления «пятёрки» меньше 1/6?
Задача 1.3.
Для проверки качества деталей из большой партии выбрали 200 деталей. Из них 12 оказались бракованными. Считается, что партия качественная, если она содержит не более 5% брака. Можно ли на уровне доверия 0,95 считать, что эта партия качественная?
Задача 1.4.
Из 635 зафиксированных отделом ГАИ ДТП 132 произошло по вине водителей-женщин. Учитывая, что по статистике доля женщин за рулём составляет 30% от общего числа водителей, можно ли считать, что женщины водят аккуратнее мужчин?
Задача 1.5.
Социологический опрос 1000 человек показал, что 65 человек собираются голосовать за партию «Справедливая Россия». На уровне значимости 5% проверить, преодолеет ли партия на выборах 7%-ный барьер.
Гипотеза об однородности в двухвыборочных задачах. Задача о сдвиге.
Задача 2.1.
Изучается влияние кобальта на увеличение массы тела кроликов. Опыт проводился на двух группах животных – контрольной и опытной. Возраст животных 1,5-2 месяца, исходная масса 500–600 г. Пищевой рацион в обеих группах одинаков, но опытной группе в пищу добавляли 0,06 г хлористого кобальта на 1 кг массы тела. Прибавка в массе в граммах составила:
560, 580, 600, 420, 530, 490, 570, 740 в контрольной группе;
692, 700, 621, 640, 561, 680, 630 в опытной группе.
Можно ли утверждать, что добавка хлористого кобальта оказывает влияние на увеличение массы тела кроликов?
Задача 2.2.
Для проверки гипотезы о том, что жители городов имеют в среднем более высокое давление, чем жители сельской местности, было проведено обследование 10 горожан и 9 жителей села примерно одного возраста. Получены следующие данные об уровне давления:
для горожан: 130, 110, 120, 140, 200, 130, 140, 170, 160, 140;
для селян: 120, 190, 130, 160, 150, 120, 110, 120, 200.
Можно ли считать верной выдвинутую гипотезу на уровне значимости 0,05?
Задача 2.3.
Уровень гистамина в мокроте у 7 курильщиков, склонных к аллергии, составил в мг:
| 102,4 | 100,0 | 67,6 | 65,9 | 64,7 | 39,6 | 31,2 |
У 10 курильщиков не склонных к аллергии составил в мг:
| 48,1 | 45,5 | 41,7 | 35,4 | 29,1 | 18,9 | 58,3 | 68,8 | 71,3 | 94,3 |
Можно ли считать, что уровень гистамина у курильщиков, подверженных аллергии выше, чем у не подверженных аллергии?
Задача 2.4.
Средняя стоимость лечения одного пациента-льготника с диагнозом «дуоденит» составляет (в рублях на ноябрь 2007 года):
| Дальневосточный фед. округ | Приволжский фед. округ |
| Амурская обл. 245,61 | Кировская обл. 196,27 |
| Еврейская АО 101,45 | Оренбургская обл. 309,79 |
| Камчатская обл. 202,84 | Пензенская обл. 271,76 |
| Корякский АО 327,63 | Пермская обл. 329,58 |
| Магаданская обл. 144,5 | Башкортостан 233,49 |
| Приморский край 458,81 | Марий-Эл 298,24 |
| Мордовия 311,6 | |
| Татарстан 284,03 | |
| Чувашия 405,5 |
Одинакова ли средняя стоимость лечения льготников в Дальневосточном и Приволжском федеральных округах?
Дисперсионный анализ. Задача однофакторного анализа.
Задача 3.1.
Для выяснения влияния денежного вознаграждения на производительность труда 30 испытуемым, разбитым на шесть однородных группам по пять человек в каждой, было предложено решить по 30 задач одинаковой трудности. Задачи предлагались каждому испытуемому независимо от всех остальных. Группы отличаются между собой величиной денежного вознаграждения за решённую задачу. В таблице приведена информация о том, сколько задач решили испытуемые.
| Группа 1 | Группа 2 | Группа 3 | Группа 4 | Группа 5 | Группа 6 |
Можно ли считать, что денежное вознаграждение влияет на количество решённых задач?
Таблица рангов:
| Группа 1 | Группа 2 | Группа 3 | Группа 4 | Группа 5 | Группа 6 |
| 5,5 | 27,5 | 23,5 | |||
| 5,5 | 21,5 | ||||
| 3,5 | |||||
| 11,5 | 11,5 | 3,5 | 21,5 | ||
| 23,5 | 27,5 |
Задача 3.2.
Для изучения влияния минерального удобрения на урожайность пшеницы был проведён эксперимент: на части засеянных пшеницей участков опытного хозяйства в почву было внесено плановое количество удобрения, на части – в два раза меньше планового, а на части удобрение не добавлялось вообще. Данные об урожайности (в центнерах с гектара) приведены в таблице:
| урожайность | |||||||
| Плановое кол-во | 28,1 | 27,0 | 26,4 | 25,7 | 26,3 | 27,6 | |
| Меньше планового | 27,2 | 26,0 | 24,7 | 24,5 | 25,1 | 26,2 | |
| Без удобрения | 24,7 | 24,9 | 23,6 | 25,4 | 25,5 | 24,2 | 24,9 |
Влияет ли добавление удобрения на урожайность?
Задача 4.1.
В одном американском учреждении изучалась связь между уровнем интеллекта девушек и наличием у них интереса к автомобилям. Было опрошено 190 старшекурсниц в пригородном высшем учебном заведении. Получены следующие данные:
| Величина IQ | Отношение к автомобилям | ||
| Нет интереса | Умеренный интерес | Большой интерес | |
| 111 и выше | |||
| 101-110 | |||
| Ниже 101 |
Можно ли сказать, что величина IQ и отношение к автомобилям связаны друг с другом?
Прокомментируйте характер связи с помощью коэффициентов Пирсона, Крамера, среднеквадратической сопряженности, мер прогноза Гутмана.
Задача 4.2.
Проведен социологический опрос 655 человек. Каждый из опрошенных отвечал на два вопроса. Вопрос А: «Удовлетворены ли Вы своим образом жизни?» (варианты ответов: да, нет). Вопрос В: «Каково Ваше материальное положение?» (варианты ответов: плохое, ниже среднего, среднее, выше среднего, хорошее. Результаты опроса сведены в следующую таблицу:
| B A | плохое | ниже среднего | среднее | выше среднего | хорошее |
| Нет | |||||
| Да |
Имеется ли зависимость между материальным положением (признак В) и удовлетворенностью образом жизни (признак А) ?
Прокомментируйте характер связи между А и В с помощью коэффициентов Пирсона, Крамера, среднеквадратической сопряженности, мер прогноза Гутмана, мер прогноза Краскела-Гудмана.
Задача 4.3.
По данным исследования «Мониторинг социальных и экономических перемен в России» составлена следующая таблица сопряженности. Вопрос А: «Как бы Вы оценили в настоящее время материальное положение вашей семьи? (Хорошее, среднее, плохое).
Вопрос В: «Как бы Вы оценили в целом политическую обстановку в России? (Благополучная, напряжённая, взрывоопасная критическая).
| B A | благоприятная | напряжённая | критическая взрывоопасная |
| хорошее | |||
| среднее | |||
| плохое |
Имеется ли зависимость между признаками А и В? Прокомментируйте характер связи между А и В с помощью коэффициентов Пирсона, Крамера, среднеквадратической сопряженности, мер прогноза Гутмана, мер прогноза Краскела-Гудмана.
Задача 4.4.
Изучается зависимость выбираемой абитуриентами специальности от пола. Было опрошено 900 человек и получены следующие результаты:
| Пол Специальность | М | Ж | |
| Естественные науки | |||
| Соц.-эконом. науки. | |||
| Искусствоведение, музыка | |||
Задача 4.5.
Есть предположение о том, что род занятий человека связан с желанием продвинуться по службе. Чтобы выяснить, справедливо ли оно, было проведено исследование и получены следующие результаты:
| Желание продвинуться Род занятий | Есть | Нет | |
| «Белые воротнички» | |||
| Квалифицированные рабочие | |||
| Полуквалифицированные рабочие | |||
Задача 6.6.
Изучается взаимосвязь между зоркостью правого и левого глаза. По результатам обследования 3242 мужчин в возрасте 30-39 лет получены следующие данные о зоркости:
| Левый глаз Правый глаз | высшая | вторая | третья | низшая | |
| высшая | |||||
| вторая | |||||
| третья | |||||
| низшая | |||||
Задача 5.1.
Изучалась зависимость между наличием у детей способностей к математике и к музыке. В эксперименте участвовало 10 детей. Преподаватель математики расставил детей в порядке их способностей от меньшего к большему: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Учитель музыки проранжировал этих детей следующим образом: 6, 5, 1, 4, 2, 7, 8, 10, 3, 9. Можно ли считать на уровне доверия 0,95, что способности к математике и к музыке связаны?
Задача 5.2.
Группа пловцов из 15 человек принимает участие в местной спортивной олимпиаде. В программе состязаний два заплыва: 50 м вольным стилем и 100 м баттерфляем. Результаты соревнований следующие:
| № | |||||||||||||||
| 50 м вольн. | 22,49 | 22,56 | 23,45 | 22,58 | 24,3 | 24,2 | 23,47 | 23,5 | 24,48 | 25,02 | 23,04 | 23,24 | 25,2 | 24,61 | 26,02 |
| 100 м батт. | 52,93 | 53,4 | 53,7 | 53,36 | 61,8 | 55,2 | 53,54 | 58,33 | 60,4 | 60,3 | 54,28 | 53,6 | 62,24 | 54,45 | 61,52 |
Пользуясь ранговым коэффициентом Спирмена определить степень связи между результатами в разных заплывах.
Задача 5.3.
Используя данные задачи 10.2, выясните являются ли среднемесячные температуры января в городах Саратове и Алатыре зависимыми.
Задача 5.4.
Запишите на доске рост (переменная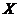 
) и средний балл на экзаменах (переменная 
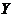) всех присутствующих студентов. По имеющимся результатам эксперимента выясните, являются л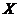и и 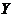зависимыми переменными.
Задача 6.1.
За кандидата на выборную должность по предварительным данным собираются голосовать от 30 до 40% избирателей. Как велико должно быть количество опрошенных жителей этого избирательного округа, чтобы можно было оценить долю голосов за данного кандидата с точностью не менее 0,01 на уровне доверия 0,95?
Задача 6.2.
Предлагается перенести начало вечерней телепередачи «Новости» на час позже. Сколько телезрителей нужно опросить, чтобы с вероятностью 0,96 оценить долю сторонников этого предложения с точностью до 0,03?
Задача 6.3.
В некотором районе, насчитывающем 5000 домохозяйств, нужно оценить с точностью до 2% процент домохозяйств, имеющих два автомобиля. По предварительным данным истинный процент таких домохозяйств колеблется между 5% и 10%. Как велико должно быть количество обследованных домохозяйств, чтобы с вероятностью 0,97 можно было получить оценку с указанной точностью?
Задача 6.4.
В посёлке проживает 2000 семей. Нужно оценить долю семей, имеющих компьютер с точностью до 0,03 на уровне доверия 0,99. Сколько семей надо опросить?
Задача 6.5.
Численность работающего населения города равна 170400 чел. Планируется провести исследование, чтобы установить долю людей, продолжительность поездки на работу у которых превышает полчаса. Сколько человек нужно опросить, чтобы с вероятностью 0,95 оценить эту долю с точностью 3%?
Задача 6.6.
Результаты выборочного обследования жилищных условий жителей города по итогам всеобщей переписи 1989 года показали, что 10,3% жителей имеют жилую площадь меньше 10 кв. м на человека. Сколько жителей нужно опросить в этом году, чтобы с вероятностью 0,99 оценить долю людей, имеющих жилплощадь меньше 10 кв. м с точностью 0,01?
Задача 6.7.
Планируется провести опрос, чтобы с точностью до 0,5% на уровне доверия 0,05 спрогнозировать, пройдёт ли партия ЛДПР 7%-й барьер на выборах в Государственную Думу. Сколько избирателей нужно опросить для этого
а) в масштабах всей страны;
б) в посёлке с населением 6 тыс. человек?
Задача 6.8.
Известно, что 2% населения города больны туберкулёзом. Сколько жителей этого города нужно обследовать, чтобы среди обследуемых больные туберкулёзом составляли 2 ± 0,2% с вероятностью 0,99?
Задача 6.9.
На последних выборах в N-кой области партия Х получила 30% голосов избирателей в городах и 70% голосов в сельских регионах. Сколько нужно опросить избирателей области, чтобы оценить поддержку партии Х на ближайших выборах с точностью до 3% с вероятностью 0,95? Городское население в области составляет 60%.
Задача 6.10.
Среди пользующихся общественным транспортом города А 60% – работающие, 25% – пенсионеры и 15% – учащиеся. Необходимо с точностью до 3% оценить процент пользующихся маршрутным такси на уровне доверия 0,97. Сколько нужно опросить людей, если по предварительным сведениям маршрутками пользуются 40% пенсионеров, 60% учащихся и 80% работающих.
Задача 6.11.
Сколько избирателей нужно опросить для этого, чтобы с точностью до 0,5% на уровне доверия 0,95 спрогнозировать, пройдёт ли партия ЛДПР 7%-й барьер на выборах в Государственную Думу. Известно, что на предыдущих выборах партию поддержало 5% пенсионеров, 11% работающих людей и 6% студентов. Доля пенсионеров среди избирателей составляет 30%, студентов – 10%, работающих – 60%.
Типы задач, которые будут в экзаменационных билетах.
1. Задача о двоичных данных.
2. Репрезентативная выборка (с возвращением/без возвращения, однородная/расслоенная ген. совокупность).
3. Однородность выборок. Критерий Вилкоксона.
4. Однофакторный анализ.
5. Независимость признаков. Критерий хи-квадрат.
6. Независимость признаков. Критерии Спирмена и Кендала.
Задача о двоичных данных
Задача 1.1.
Известно, что вероятность рождения мальчика равна 0,52. В случайной выборке из 5000 человек в возрасте от 30 до 60 лет мужчин оказалось 2500. Можно ли считать, основываясь на этих данных, что смертность среди мужчин и женщин одинакова, рискуя ошибиться один раз из 20?
Задача 1.2.
Игральную кость подбросили 600 раз, «пятёрка» выпала 80 раз. На уровне доверия 0,95 проверить гипотезу о том, что кость правильная. Можно ли утверждать на уровне доверия 0,9, что вероятность появления «пятёрки» меньше 1/6?
Задача 1.3.
Для проверки качества деталей из большой партии выбрали 200 деталей. Из них 12 оказались бракованными. Считается, что партия качественная, если она содержит не более 5% брака. Можно ли на уровне доверия 0,95 считать, что эта партия качественная?
Задача 1.4.
Из 635 зафиксированных отделом ГАИ ДТП 132 произошло по вине водителей-женщин. Учитывая, что по статистике доля женщин за рулём составляет 30% от общего числа водителей, можно ли считать, что женщины водят аккуратнее мужчин?
Задача 1.5.
Социологический опрос 1000 человек показал, что 65 человек собираются голосовать за партию «Справедливая Россия». На уровне значимости 5% проверить, преодолеет ли партия на выборах 7%-ный барьер.