Показатели вариации и анализ частотных распределений

По действующей методике государственной кадастровой оценке земель сельскохозяйственного назначения при определении удельных показателей кадастровой стоимости земельных участков особое место занимают показатели качества земель или их технологические свойства, которые оцениваются по природной выраженности - разнородному проявлению факторов урожайности и затрат, и обобщаются на земельных участках по эффективности производства продукции. По одному из указанных факторов – урожайности - определим показатели ее вариации и проведем анализ частотных распределений К(Ф)Х.

Построим нормальное распределение по эмпирическим данным. Имея дело с эмпирическим распределением, можно предположить, что данному распределению соответствует определенная, характерная для него теоретическая кривая. Подобрав форму распределения – нормальное распределение 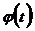- опишем эмпирический ряд с помощью математической модели, выражающий теоретический закон распределения.

Нормальным 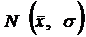называют распределение непрерывной случайной величины x, если соответствующая ее плотность распределения выражается формулой Гаусса-Лапласа:

,

где 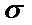- дисперсия (средний квадрат отклонений индивидуальных значений признака от средней арифметической); 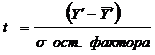- нормированное отклонение; 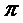- постоянное число, которое равно 3.1415; 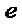- основание натурального логарифма, равное 2.7182, и изображается графиком нормального распределения.

Случайные величины, распределенные по нормальному закону, различаются значениями параметров 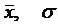, поэтому важно выяснить, как эти параметры влияют на вид нормальной кривой. Кривая, отображающая это распределение, имеет вид колокола, она симметрична. В зависимости от значений 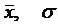она может иметь разный центр группирования, т.е. быть более удлиненной или сжатой.

Главная особенность нормального распределения состоит в том, что оно является предельным, к которому приближаются другие распределения. Нормированное отклонение характеризует колеблемость отдельных вариантов, выраженных в среднеквадратических отклонениях.

Весь математический анализ проведем на примере распределения К(Ф)Х по урожайности картофеля (таблицы 2.12, 2.13).

Определяем по эмпирическим данным параметры кривой нормального распределения:

1. Находим среднюю урожайность картофеля:

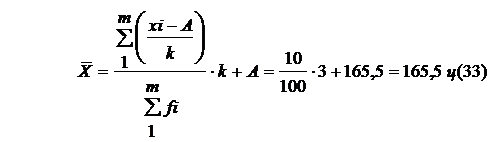
где А – середина интервала (Хi) – графа 3; k – шаг интервала, равный 3 – (таблица 2.12 графа 2).

Таблица 2.12

Расчет дисперсии способом отчета от условного нуля

№ п.п	Группы по урожайности картофеля, ц X	Число К(Ф)Х, fi	Середина интервала Xi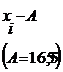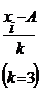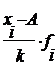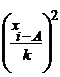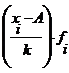
	143-146		144,5	- 21	- 7	- 7
	146-149		147,5	- 18	- 6	- 12
	149-152		150,5	- 15	- 5	- 40
	152-155		153,5	- 12	- 4	- 104
	155-158		156,5	- 9	- 3	- 195
	158-161		159,5	- 6	- 2	- 240
	161-164		162,5	- 3	- 1	- 181
	164-167		165,5
	167-170		168,5
	170-173		171,5
	173-176		174,5
	176-179		177,5
	179-182		180,5
	182-185		183,5
	185-188		186,5
	Итого		-	-	-		-

٭ - А –середина интервального ряда

2. Определяем среднее квадратическое отклонение (таблица 2.13 графа 9):

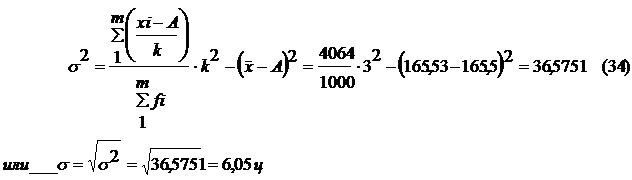
Таким образом, каждое конкретное значение урожайности картофеля отклоняется от среднего на 6,05 ц.

3. Определяем нормированное отклонение t для каждого К(Ф)Х (таблица 2.13 .графа 6).

4. По таблице распределения функции 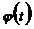(приложение 1) определяем ее значение (таблица 2.13 графа 7).

Таблица 3.13

Распределение К(Ф)Х по урожайности картофеля

№ п.п	Группы по урожайности картофеля, ц (X)	Число К(Ф)Х, (fi)	Середина интервала (Xi)		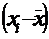		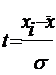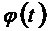Теоретические частоты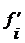
	143-146		144,5	- 21	3,47	0,0010
	146-149		147,5	- 18	2,98	0,0047
	149-152		150,5	- 15	2,48	0,0184
	152-155		153,5	- 12	1,98	0,0562
	155-158		156,5	- 9	1,49	0,1315
	158-161		159,5	- 6	0,99	0,2444
	161-164		162,5	- 3	0,50	0,3525
	164-167		165,5		0,00	0,3989
	167-170		168,5		0,50	0,3525
	170-173		171,5		0,99	0,2444
	173-176		174,5		1,49	0,1315
	176-179		177,5		1,98	0,0562
	179-182		180,5		2,48	0,0184
	182-185		183,5		2,98	0,0047
	185-188		186,5		3,47	0,0010
	Итого		-	-	-	-

5. Определяем теоретические частоты 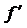по формуле:

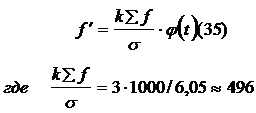
Полученное значение 496 умножаем на величину 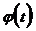при данном t и получим искомую теоретическую частоту (графа 8).

6. Сравниваем на графике (рис.2.8) эмпирические 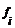и теоретические 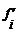, полученные на основании данных таблицы 2.13. Ряд 1 на рисунке обозначает теоретические значения признака; ряд 2 – фактические значения признака.

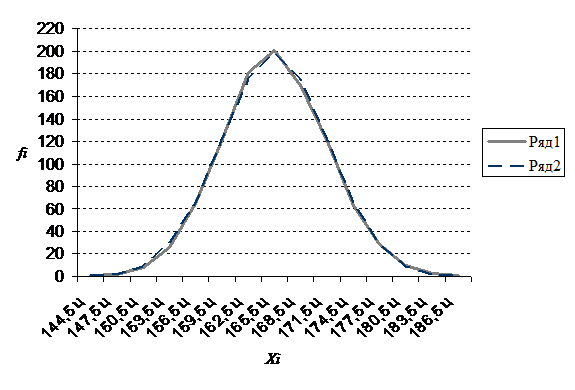
Рис. 2.8. Диаграмма распределения К(Ф)Х по урожайности картофеля

После изучения раздела 2.4 студент сможет:

- обосновать обобщающие показатели вариации, их значение, содержание и методику расчета;

- применять законы вариации и распределения.

Выборочное наблюдение

Значительная часть задач статистики связана с необходимостью описать большую совокупность объектов, которую называют генеральной. Генеральной совокупностью называют множество результатов всех мыслимых наблюдений над значениями одного или нескольких признаков, которые могут быть сделаны при данном комплексе условий. При этом комплекс условий определяет вариацию признаков генеральной совокупности. Синонимом генеральной совокупности в статистике является случайная величина . Выборочной совокупностью (выборкой) называют множество результатов, случайно отобранных из генеральной совокупности. Выборка должна быть репрезентативной, т.е. правильно отражать пропорции генеральной совокупности. Это достигается случайностью отбора, когда все объекты генеральной совокупности имеют одинаковую вероятность быть отобранными.

Различают два вида отбора – повторный и бесповторный. При первом каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. При бесповторном отборе каждая отобранная единица в генеральную совокупность не возвращается. Оба способа могут быть реализованы в следующих основных видах выборки:

- собственно случайная, проводится по таблицам случайных чисел;

- механическая, реализуется по нейтральным спискам единиц отбора;

- типическая (стратифицированная, районированная);

- серийная, при которой отбираются серии или гнезда и в них обследуются все единицы;

- комбинированная или многоступенчатая, где выборочная совокупность формируется постепенно, по ступеням отбора;

- многофазная, формируемая из ряда последовательных подвыборок;

- взаимопроникающая – это две или более независимые выборки из одной и той же совокупности, образованные одним способом и видом.

Проведем выборку (повторную) на примере объектов капитального строительства, расположенных на территории нескольких городов Московской области, общим количеством в 10 000 ед. Из них в городе А – 5000, в городе Б – 3000, в городе С – 2000. С целью определения средней площади занимаемого ими земельного участка применяем типическую выборку объектов капитального строительства с пропорциональным отбором внутри групп (механическим). Вначале следует определить какое количество объектов капитального строительства необходимо отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 единиц, если известно, что дисперсия типической выборки равна 1600.

Рассчитываем необходимое количество типической выборки по таблице «Нормального закона распределения. Значение функции » (приложение 2) найден t= 2,0.

По формуле определения объема выборки при заданном способе ее формирования определяем:

где t– критерий доверия, в расчетах обычно берется в пределах от 2 до 3, что соответствует вероятности от 0,954 до 0,997; N– объем генеральной совокупности ; l– число типических групп; - дисперсия доли изучаемого признака в выборочной совокупности.

Необходимо отобрать 250 объектов капитального строительства, из них в городе А: (ОКС), в городе Б: (ОКС), в городе С: (ОКС).

После изучения раздела 2.5 студент сможет:

- описать способы и виды выборки;

- обосновать научные основы и этапы выборочного наблюдения;

- привести и объяснить формулу расчета необходимой численности выборки.