Насаждение, состоящее из одной породы, называется чистым, из двух или нескольких пород - смешанным.
Породный состав простого насаждения или яруса в сложном насаждении устанавливается по доле участия запасов составляющих древесных пород (элементов леса) и записывается формулой, в которой приводятся сокращенные обозначения древесных пород и доли участия древесной породы в составе, выражаемая в виде коэффициента (целого числа), каждая единица которого соответствует 10% ее участия в общем запасе (100%). Древесные породы, запас которых составляет до 5% от общего запаса насаждения (яруса), записываются в формуле состава знаком “+” (плюс).
В многоярусных насаждениях породный состав устанавливается для каждого яруса.
Единичные деревья (семенники, перестой и другие), отличающиеся от основного яруса по возрасту более чем на 2 класса, резко отличающиеся по высоте и диаметру, в состав древостоя не вводятся, а учитываются отдельно как единичные деревья.
В несомкнувшихся культурах, а также в молодняках до 20 лет породный состав устанавливается по соотношению числа стволов составляющих пород.
Если в пологе молодняка имеются подлесочные породы, то они в формулу состава не вводятся и не учитываются при определении полноты.
Для основных лесообразующих древесных пород устанавливаются следующие сокращенные обозначения: сосна - С, ель - Е, пихта - П, лиственница - Л, кедр - К, дуб - Д, бук - Бк, граб - Г, ясень - Я, клен - Кл, ильм - Ил, вяз - В, берест -Бр, береза - Б, осина - Ос, ольха черная - Олч, ольха серая - Олс, липа - Лп, тополь - Т, ива - Ив (ивы древовидные - Ивд, ивы кустарниковые - Ивк).
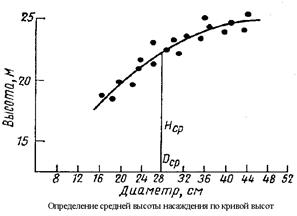
Средняя высота насаждений.
 |
Высота деревьев в любом насаждении не одинакова. В пределах насаждения различия в высоте наблюдаются не только у деревьев разной толщины, но они имеют место и у деревьев равных диаметров.
В процессе таксации леса учесть индивидуальную высоту каждого дерева не представляется возможным. В связи с этим принято устанавливать среднюю высоту для всей совокупности деревьев, образующих насаждение.
В более или менее однородных насаждениях все же наблюдается стохастическая (вероятностная) зависимость высоты деревьев от их диаметров. С увеличением последних у большинства деревьев соответственно растет и высота. Гогенадль, Кренн и другие исследователи связь между d1,3 и h в насаждении характеризуют уравнением параболы второго порядка.
Профессором Лореем предложена следующая формула, определяющая среднюю высоту насаждения:
hL = 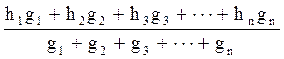 ,
,
где hL - средняя высота;
h1 . . . hn - высота для отдельных ступеней толщины;
g1 . . . gn - площади сечения деревьев каждой ступени толщины.. Средняя высота насаждений зависит от древесной породы, условий местопроизрастания, возраста и осуществляемых в лесу хозяйственных мероприятий. В пределах насаждения различия в высоте обусловливаются разным положением деревьев в отношении света, смежных деревьев, микроповышений и почвенных разностей. Влияние перечисленных факторов на высоту деревьев не имеет количественно выраженных зависимостей, и 'их установление представляет трудную задачу. При одном и том же диаметре деревьев в пределах насаждения высоты оказываются разными. Из-за конкуренции за свет
распределение деревьев по высоте показывает положительную асимметрию.
Однако стохастические связи между h и d позволяют строить кривые высот на основе небольшого количества измерений, но дающих достаточно точные оценки высот для практических и научных целей.
Средняя высота, определяемая по формуле Лорея, как таксационный показатель имеет недостаток, заключающийся в том, что на ее величину оказывает влияние вырубка части деревьев при уходе за лесом.
Если этот уход ведется низовым способом, заключающимся в изъятии из насаждения отставших в росте более мелких деревьев, то средняя высота насаждения после ухода за ним увеличивается.
При проведении верхового способа ухода за лесом вырубаются более крупные деревья. Соответственно этому обстоятельству после проведения таких рубок средняя высота насаждения уменьшается.
В западноевропейских странах все большее значение придают «доминирующей высоте деревьев», не зависящей от режима ухода за лесом.
На французском языке этот таксационный показатель носит название «hauteur dominante» — доминирующая высота.
В немецкой лесотаксационной литературе ее называют Oberhohe — верхняя высота.
Для доминирующей высоты принято международное обозначение hdom.
В Англии за доминирующую берут среднюю высоту 100 наиболее толстых деревьев на площади насаждения в один акр. Один гектар в 2,47 раза больше акра. Соответственно этому для площади в 1 га средняя высота 247 наиболее толстых деревьев на 1 га является доминантной высотой (hdom).
Однако большинство исследователей и по отношению к одному гектару в качестве доминантной высоты берут среднюю из 100 наиболее крупных деревьев.
В СССР было разработано несколько новых методов определения верхней высоты. Б.Б. Зейде в 1970 г. предложил метод переменной доли, когда доля деревьев, измеренных для нахождения верхней высоты зависит от варьирования диаметров. Этот метод долгое время был принят в качестве стандартного.
Среднюю высоту находят путем построения кривой. С этой целью обмеряют диаметры и высоту у ряда деревьев, отобранных тем или иным путем. По результатам этих обмеров находят аналитическое уравнение.
При построении кривых высот рекомендуется вычислять на основе обмеренных высот средние высоты по ступеням толщины и проводить плавную кривую через средние значения. Пользуясь кривой высот, можно найти высоту деревьев любого диаметра. Для этого из точки на оси абсцисс, соответствующей диаметру данного дерева, надо восставить перпендикуляр до пересечения с кривой высот. Длина этого перпендикуляра (ординаты), увеличенная соответственно масштабу, в котором нанесены высоты, является искомой высотой дерева.
Уравнения связи Н = f (Д) описываются разными уравнениями: полиномы от 2 до 4 степени, логарифмические кривые (простые и сложные), степенные и показательные функции.
Можно среднюю высоту найти как среднеарифметическую величину. Но это будет чисто статистическая величина. Она не будет характеризовать среднее дерево по диаметру и запасу.
В целом hариф < hg < hw < hg m < hл < hв.
В практике среднюю высоту определяют, измеряя 12-15 деревьев методом случайной выборки и строя кривую высот.
В производственных условиях среднюю высоту для нахождения разряда высот определяют, измеряя 9 деревьев: 3 из центральной ступени толщины и по 3 из соседних. Варьирование высот в приспевающих и спелых древостоях составляет 6-8%. Следовательно, измеряя 12-15 деревьев мы определим Hср с точностью около 2%, а при 9 замерах 2-3%.
В разновозрастных, многоярусных древостоях Hср находят для каждого яруса. В смешанном древостое измерения делают для каждой породы.
Опытный таксатор после ежегодно проводимых тренировок среднюю высоту определяет глазомерно.
Возраст насаждений.
При таксации леса различают преобладающий и средний возраст насаждения. Преобладающим называют возраст, который имеет большая часть деревьев, образующих насаждение, средним — возраст, выведенный пропорционально участию в запасе отдельных групп деревьев, входящих в состав насаждения.
В лесной таксации насаждения по возрасту делятся на классы. Для хвойных и твердолиственных семенных насаждений устанавливают класс возраста 20 лет, для всех порослевых и мягколиственных семенных насаждений 10 лет (табл. 8.1), для кустарниковых пород 5 лет. Классы возраста обозначают всегда римскими цифрами.
Разделение насаждений на классы возраста
| Возраст в годах | Возраст в годах | ||||
| Клас-сы возраста | Хвойные и твердолиственные породы семенного происхождения | Мягкие и твердолиственные породы порослевого про-исхождения | Клас- сы воз- раста | Хвойные и твердолиственные породы семенного происхож-дения | Мягкие и твердолиственные породы порослевого происхождения |
| I | 1-20 | 1-10 | IV | 61-80 | 31-40 |
| II | 21-40 | 11-20 | V | 81-100 | 41-50 |
| III | 41-60 | 21-30 | VI | 101-120 | 51-60 |
В последнее время в южных и западных странах для хвойных пород установлены классы возраста 10 лет.
При описании насаждений класс возраста устанавливают по той части деревьев, которые составляют большую часть запаса насаждения. Если деревья в насаждении имеют разницу в возрасте, нe превышающую длительности одного класса возраста (табл. 8.1), насаждение считается одновозрастным, при большей разнице в возрасте — разновозрастным.
В таксационном описании в графе «Возраст насаждений» кратко указывают класс возраста и преобладающий возраст, например, IV—65, V—90. В отдельной графе, предназначенной для подробного описания состава и возраста насаждений, делают запись о наличии примеси деревьев, имеющих иной возраст.
В таксационных описаниях запись состава и возраста насаждения нередко объединяют в одну формулу. Например, при возрасте сосны 90 лет и ели 70 лет, когда эти породы образуют один ярус, формула состава и возраста имеет следующий вид: 7С(90)ЗЕ(70).
В широкой таксационной практике ориентировочный возраст насаждений нередко определяют по внешним признакам дерева: цвету хвои, форме кроны, цвету и строению коры. У старых деревьев хвойных пород окраска хвои более светлая, чем у молодых. У прекративших рост в высоту старых деревьев крона обычно имеет закругленную шапкообразную и куполообразную форму, нижняя часть ствола покрыта толстой растрескавшейся омертвевшей корой. В трещины коры таких деревьев попадают пыль и влага, являющиеся субстратом для роста и развития водорослей и других низших растений. В результате комлевая часть стволов покрывается наростами зеленого, желтого и других цветов.
Для молодых деревьев характерны усиленный рост в высоту, шпилеобразная форма кроны, гладкая глянцевитая кора. У деревьев хвойных пород хвоя сочная, темно-зеленой окраски.
Преобладающий возраст насаждения определяют глазомерно. Особенности колебаний возраста отмечают в формуле состава насаждения. При интенсивном росте насаждений возраст определяют глазомерно с точностью до 5 лет, при среднем - до 10 лет, при слабом - до 20 лет.
В процессе таксационных работ результаты глазомерного определения возраста должны систематически проверяться путем подсчета годичных слоев на пнях и на всех срубаемых на визирах деревьях.
Бонитет насаждений.
Лес произрастает в разнообразных климатических и почвенных условиях. Поэтому он имеет разную продуктивность, которую необходимо учитывать при таксации.
В лесной таксации для оценки условий роста леса устанавливают «бонитет насаждения». Термин этот происходит от латинского слова bonitas, что означает «доброкачественность».
Следовательно, бонитет является показателем, характеризующим качество условий произрастания леса.
Различие в условиях произрастания леса в таксации характеризуют несколькими классами бонитета, обозначаемыми порядковыми номерами: I класс означает лучшие условия произрастания леса, а последующие — их постепенное ухудшение. Деление леса на классы бонитета основано на определенных признаках.
В условиях произрастания леса решающую роль играет качество почвы (структура, химический состав, содержание гумуса, степень увлажнения, мощность почвенного слоя и др.). Поэтому при установлении класса бонитета, казалось бы, характеристика почвы, на которой произрастает насаждение, должна быть определяющим фактором. Так именно и подходили к установлению класса бонитета, именовавшегося тогда классом добротности, в середине XIX в. при составлении первых русских таблиц, характеризовавших динамику роста и развития насаждений. Однако попытка классификации условий местопроизрастания и определения класса бонитета в зависимости от почвенных условий положительных результатов не дала.
Соответствие между почвенными признаками и классами бонитета установить довольно трудно. С одной стороны, в один и тот же класс бонитета попадали различные почвы, а с другой — почвы, одинаковые по внешним признакам, относились к разным классам бонитета.
Позднее был использован опыт сельского хозяйства, в практике которого довольно часто плодородие почвы, или степень пригодности для выращивания отдельных видов сельскохозяйственных культур, оценивается величиной урожая, собираемого с единицы площади. Отсюда лучшие условия местопроизрастания, относимые к высшим классам бонитета, при прочих равных условиях должны обеспечивать наибольшие годичный прирост и общую продуктивность леса, наибольший запас на единице площади, а с ухудшением условий местопроизрастания все эти показатели соответственно должны уменьшаться.
Многолетние опыты и наблюдения говорят о том, что лучшим показателем, отображающим качество условий местопроизрастания, является высота насаждения в определенном возрасте. Чем больше средняя высота насаждения, тем лучше, следовательно, условия местопроизрастания. Поэтому в качестве классификационного признака для деления насаждений на классы бонитета с 1911 г. в русской таксационной практике используют среднюю высоту.
Средняя высота насаждений зависит и от их возраста: с увеличением возраста она соответственно увеличивается. Поэтому среднюю высоту с учетом возраста используют для установления класса бонитета.
Профессор М.М. Орлов, разработавший бонитировочную шкалу, предложил разделять насаждения на пять классов бонитета. К крайним классам (I и V) в этом случае относятся насаждения, хотя и редко встречающиеся, но с широкой амплитудой колебания высоты. Чтобы устранить этот недостаток, из I и V классов выделили дополнительные литерные классы 1а и Va. Таким образом, было установлено всего семь классов. В тех случаях, когда насаждения 1а и Va классов занимают незначительную площадь, они могут быть объединены с основными пятью классами.
Шкала деления насаждений на классы бонитета, разработанная профессором М.М. Орловым, имеет два входа: возраст насаждений и среднюю высоту. Разным сочетаниям этих двух элементов соответствует определенный класс бонитета.
Пределы изменения средней высоты семенных насаждений по классам бонитета (по М. М. Орлову)
| Возраст, | Высота насаждений по классам бонитета | ||||||
| лет | Iа | I | II | III | IV | V | Vа |
| 6—5 | 5—4 | 4—3 | 3—2 | 2—1 | |||
| 12—10 | 9—8 | 7—6 | 6—5 | 4—3 | |||
| 16—14 | 13—12 | 11—10 | 9—8 | 7—6 | 5—4 | 3—2 | |
| 20—18 | 17—15 | 14—13 | 12—10 | 9—8 | 7—5 | 4—3 | |
| 24—21 | 20—18 | 17—15 | 14—12 | 11—9 | 8—6 | 5—4 | |
| 28—24 | 23—20 | 19—17 | 16—14 | 13—11 | 10—8 | 7—5 | |
| 30—26 | 25—22 | 21—19 | 18—16 | 15—12 | 11—9 | 8—6 | |
| 32—28 | 27—24 | 23—21 | 20—17 | 16—14 | 13—11 | 10—7 | |
| 34—30 | 29—26 | 25—23 | 22—19 | 18—15 | 14—12 | 11—8 | |
| 35—31 | 30—27 | 26—24 | 23—20 | 19—16 | 15—13 | 12—9 | |
| 36—32 | 31—29 | 28—25 | 24—21 | 20—17 | 16—13 | 12—10 | |
| 38—34 | 33—30 | 29—26 | 25—22 | 21—18 | 17—14 | 13—10 | |
| 39—35 | 34—31 | 30—27 | 26—23 | 22—19 | 17—14 | 13—10 | |
| 40—36 | 35—31 | 30—27 | 26—23 | 22—19 | 18—14 | 13—10 |
Шкала деления насаждений на классы бонитета является общей для всех древесных пород, хотя в росте отдельных пород, особенно в молодом возрасте, наблюдаются отклонения от нее. Единая шкала для бонитирования всех насаждений упрощает таксационные работы и позволяет сравнивать получаемые результаты.
Интенсивность роста семенных и порослевых насаждений неодинакова: семенные растут в раннем возрасте медленнее. Для определения класса бонитета семенных и порослевых насаждений установлены особые шкалы. В таблице. дана шкала деления на классы бонитета семенных насаждений.
Ряд авторов предложили свои усовершенствованные бонитетные шкалы. Профессор К.Е. Никитин в 1965 г. предложил более плавную шкалу, описываемую математически. Профессор В.В. Загреев и другие авторы предложили 3 бонитетных шкалы: с ускоряющимся ростом, с обычным и замедленным ростом.
Основной недостаток шкалы М.М. Орлова в том, что одно насаждение в течение жизни может соответствовать разным классам бонитета.
Несмотря на все недостатки, до сих применяется шкала М.М.Орлова.
В зарубежных странах проводится бонитирование как по средней высоте, так и по верхней. За базовый возраст тоже берут разные значения, например, в США - 50 лет. В США за базовую берут высоту 100 футов в 50 лет, а все следующие классы уменьшают на 10 футов, минимум - 50 футов. В Англии бонитетные шкалы есть для каждой породы. В общем, разнообразие большое, но основной признак связь НотА сохраняется.
Полнота насаждений.
 |
Деревья в лесу имеют разную густоту стояния. Иногда они расположены так плотно, что их кроны соприкасаются, в других случаях образуют прогалины.
Степень плотности стояния деревьев, характеризующую, в какой мере ими использованную занимаемое пространство, принято называть полнотой насаждения. Полнота насаждения является одним из главнейших таксационных показателей, с помощью которого определяют запас насаждения.
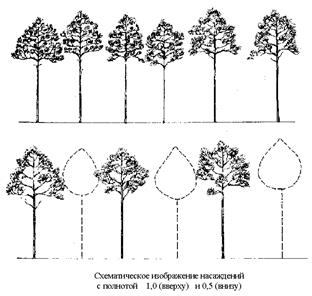
Устанавливаемые для характеристики полноты насаждения числовые показатели определяют, насколько полно использовано пространство, занимаемое образующими насаждение деревьями. Если плотность стояния деревьев настолько велика, что в просветы между ними больше нельзя поместить деревья таких же размеров, полнота насаждений считается наивысшей и обозначается 1,0, если к имеющимся деревьям можно добавить такое же число деревьев тех же размеров, полноту принимают равной 0,5 (рис. 8.7). В тех случаях, когда к имеющимся деревьям нужно добавить 0,1 часть их количества, чтобы получить число деревьев самого полного насаждения, полноту таксируемого насаждения следует считать равной 0,9 и т.д.
Полнота насаждения — величина относительная. При определении ее в качестве эталона берут так называемое нормальное насаждение.
Профессор М.М. Орлов называет нормальным такое насаждение, которое при данных форме, породе, возрасте и условиях местопроизрастания является наиболее совершенным, т.е. все силы природы использованы им с предельной полнотой. Соответственно этому в нормальном насаждении не должно быть ни одного лишнего или недостающего дерева. А это может быть, лишь если полог деревьев, образующих насаждение, вполне смыкается, кроны полностью прикрывают почву и не позволяют на этой площади расти большему числу деревьев данной породы и возраста.
Из сказанного можно заключить, что первоочередным критерием для суждения о полноте насаждения является степень сомкнутости крон деревьев, называемая сомкнутостью полога. Не следует забывать, что сомкнутость полога и полнота насаждений — понятия разные, но имеющие между собой коррелятивную связь, в большинстве случаев характеризующуюся довольно высоким коэффициентом корреляции. Сомкнутость полога зависит от породы деревьев, их биологических особенностей, возраста, условий произрастания, лесорастительной зоны и др. Например, бук и липа дают более плотное смыкание, чем береза или лиственница; более теневыносливые породы образуют иную сомкнутость, чем светолюбивые; степень смыкания у деревьев, развивающих широкую крону, и узкокронных различна и т.д. При точных таксационных исследованиях необходимо отличать сомкнутость, определяемую по площади проекции полога, от устанавливаемой по сумме площадей проекций крон. В первом случае сомкнутость представляет собой отношение площади проекции всего полога к площади участка, занимаемого насаждением, во втором она определяется как отношение суммы площадей проекций крон, учитываемых отдельно для каждого дерева, входящего в состав таксируемого насаждения, к площади, занимаемой этим насаждением.
Сомкнутость полога в северных и восточных лесах, растущих на бедных почвах, меньше, чем в средней и южной полосе.
Полноту насаждений по сомкнутости крон устанавливают глазомерно. Таксатору чаще всего приходится работать в насаждениях, где между кронами соседних деревьев имеются значительные свободные пространства. В этих случаях он должен мысленно представить, какую часть деревьев можно добавить в промежутки между имеющимися. Сначала он должен обратить внимание на неизбежные разрывы между кронами в более сомкнутых группах (гнездах) деревьев, затем на разрывы между группами отдельных деревьев (прогалины).
Глазомерным способом можно определить полноту лишь приближенно. Для более точного определения существуют другие способы.
Нормально полное для данной породы, возраста и бонитета насаждение должно иметь наивысший запас древесины. Соответственно этому полноту всех других насаждений можно определить путем деления запаса таксируемого насаждения на запас полного нормального насаждения той же породы, возраста и бонитета.
Чаще всего на таксируемой площади производят перечет деревьев и по вспомогательным таблицам определяют сумму площадей сечений на высоте груди у всех деревьев, вошедших в перечет. Затем находят сумму площадей сечения на 1 га и сравнивают ее с суммой площадей сечения нормального полного насаждения того же состава, возраста и класса бонитета, что и таксируемое насаждение.
Для главнейших древесных пород суммы площадей поперечных сечений деревьев в полных нормальных насаждениях установлены опытным путем и указаны в особых таблицах, характеризующих динамику развития насаждений — таблицах хода роста насаждений.
В этом случае полноту насаждения определяют по следующей простой формуле: P= 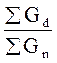 ,
,
где åGd — сумма площадей поперечных сечений деревьев,
имеющихся на 1 га данного насаждения;
åGn — сумма площадей поперечных сечений нормального
полного насаждения.
Суммы площадей сечений полных нормальных древостоев определяют, помимо таблиц хода роста насаждений, по таблицам, получившим название стандартных.
Профессор Н.В. Третьяков сумму площадей сечений деревьев, образующих древостой, называет абсолютной полнотой, а частное от деления этой суммы на соответствующую сумму площадей сечений нормального насаждения — относительной полнотой.
